Transition Edge Sensors (TES)
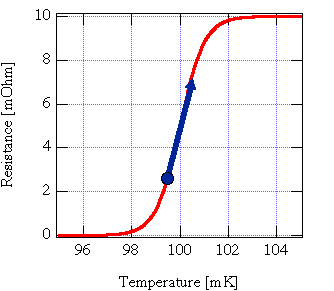
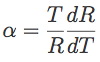
where T is the temperature and R is the resistance of the TES. The energy resolution of a TES can be approximated by
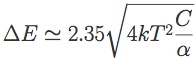
where k is Boltzmann's constant, T is the TES temperature, C is the microcalorimeter's heat capacity, α was define above, and the factor of 2.35 is to convert standard deviation into full-width at half maximum (FWHM) (just an easier way to measure the resolution of our devices). So for good energy resolution, we want to operate the devices as cold as we can, have a low heat capacity and a high α.
An important limitation is the fact that the TES operates well as a thermometer only in its transition. Once it goes normal, its resistance no longer changes with temperature (much), and α → 0. This implies a maximum temperature change in the TES, which in turn implies a maximum energy of the incoming photons:
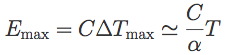
So the parameters C and α are tied by the desired energy bandpass of the microcalorimeter. We can then state the theoretical energy resolution of a microcalorimeter in a simple formula that only depends on the temperature of operation and the bandpass of the device:
For a typical X-ray application, the bandpass is from ~ 0.1 keV to 10 keV, and operating at 100 mK gives us an energy resolution of ΔE = 1.4 eV FWHM, close to two orders of magnitude better than the theoretical limits for X-ray CCDs.

