


Next: Two-dimensional Laminar Jet.
Up: No Title
Previous: Approximate Method Based on
For an ideal fluid the flow against an infinite flat plate in the plane y = 0 is given by
where U is a constant. When viscosity is included, it still must be true that u is proportional to x, for small x and for all y.Thus, for small x, at least, we may take
The governing equations for steady flow in terms of dimensional variables are given by equations (2.1) to (2.3). If we substitute equation (7.124) into the continuity equation (2.3), we obtain
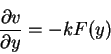 |
(125) |
This suggest that we take
Now, we substitute equations (7.126) and (7.127) into the governing equations (2.1) to (2.3). We obtain from
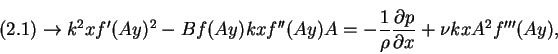 |
(128) |
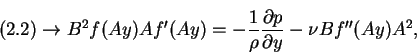 |
(129) |
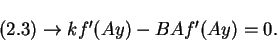 |
(130) |
This last equation implies that BA = k, so we can write equations (7.128) and (7.130) in the form
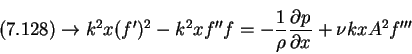 |
(131) |
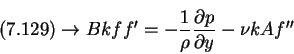 |
(132) |
We can solve equation (7.131) for the pressure derivative with respect to x to obtain
![\begin{displaymath}-\frac{1}{\rho}\frac{\partial p}{\partial x} = k^{2}x[(f')^{2}-ff''-\frac{\nu}{k}A^{2}f''']
\end{displaymath}](img178.gif) |
(133) |
Since the the term between brackets in the right side of the equation above is not a function of x, we set
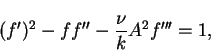 |
(134) |
which implies, according to equation (7.133), that
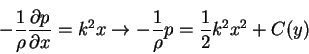 |
(135) |
If we substitute equation (7.135) into equation (7.132), we have the relation
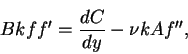 |
(136) |
and if we integrate this equation, we obtain that
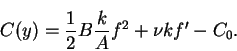 |
(137) |
Next, we substitute the expression for C(y) above into the equation (7.135) for the pressure, which gives
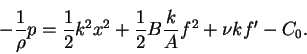 |
(138) |
To simplify equation (7.134), we chose the coefficient of f''' equal to one, which implies that
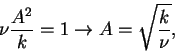 |
(139) |
and since BA = k, we have that
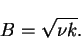 |
(140) |
With equations (7.138) and (7.139), we can write the equation (7.138) as follows
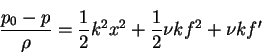 |
(141) |
with
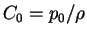 and p0 is the pressure as
and p0 is the pressure as
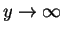 .
The function
.
The function 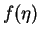 ,
where
,
where
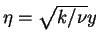 satisfies the ordinary differential equation
satisfies the ordinary differential equation
|
(f')2-ff''-f'''-1 = 0
|
(142) |
with boundary conditions:
- No slip condition at the plate surface.
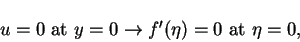 |
(143) |
- No flux across the plate:
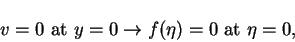 |
(144) |
- At
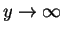 ,
we have u = kx, which implies that
,
we have u = kx, which implies that
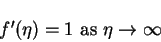 |
(145) |
In summary, the function 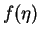 is the solution of the boundary value problem given by the equations (7.142) to (7.145), which has no closed form solution. The equation ordinary differential equation (7.142) is non-linear and has to be solved numerically together with the boundary conditions (7.143) to (7.145). Figure 2 below illustarte the result of the numerical evaluation of the boundary value problem given by equations (7.142) to (7.145) for
is the solution of the boundary value problem given by the equations (7.142) to (7.145), which has no closed form solution. The equation ordinary differential equation (7.142) is non-linear and has to be solved numerically together with the boundary conditions (7.143) to (7.145). Figure 2 below illustarte the result of the numerical evaluation of the boundary value problem given by equations (7.142) to (7.145) for 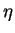 in the range
in the range
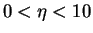 .
.
Figure:
Functions
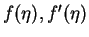 and
and 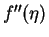 .
The horizontal axis represents the range of values of
.
The horizontal axis represents the range of values of 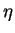 considered, and in the vertical axis we have the values of the functions
considered, and in the vertical axis we have the values of the functions
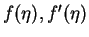 and
and 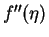 .
.
|
|
Once we know the values of
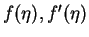 and
and 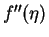 ,
we can obtain the velocities u and v given, respectivelly, by equations (7.126) and (7.127) with B and A given, respectively, by equations (7.139) and (7.140), the pressure field is given by equation (7.141).
,
we can obtain the velocities u and v given, respectivelly, by equations (7.126) and (7.127) with B and A given, respectively, by equations (7.139) and (7.140), the pressure field is given by equation (7.141).



Next: Two-dimensional Laminar Jet.
Up: No Title
Previous: Approximate Method Based on
Karl P Burr
2003-03-12
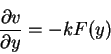
![\includegraphics[width=5.5in,height=5.5in]{ps/func_ff1f2a.eps}](img193.gif)