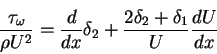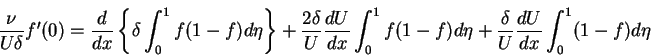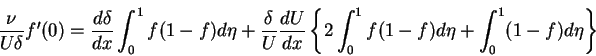Next: Stagnation Point flow. Up: No Title Previous: Energy Integral.

Approximate Method Based on the Momentum Equation: Pohlhausen's Method.

One of the earliest and, until recently, most widely used approximate methods for the solution of the boundary layer equation is that developed by Pohlhausen. This method is based on the momentum equation of Kármán, which is obtained by integrating the boundary layer equation (4.77) across the layer, as shown in section 5.1. In the case of steady flow over an impermeable surface, the momentum equation (5.93) reduces to

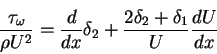$\begin{displaymath}\frac{\tau_{\omega}}{\rho U^{2}} = \frac{d}{dx}\delta_{2}+\frac{2\delta_{2}+\delta_{1}}{U}\frac{dU}{dx} \end{displaymath}$

(99)

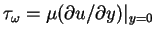where $\tau_{\omega} = \mu(\partial u/\partial y)\vert _{y=0}$ is the skin friction, 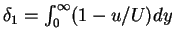$\delta_{1} = \int_{0}^{\infty}(1-u/U)dy$ is the displacement thickness, and 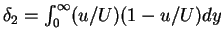$\delta_{2} = \int_{0}^{\infty}(u/U)(1-u/U)dy$ is the momentum thickness of the boundary layer. The boundary conditions for the boundary layer equations (4.77) and (4.78) are

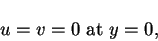$\begin{displaymath}u = v = 0 \mbox{\ at\ } y = 0, \end{displaymath}$

(100)

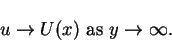$\begin{displaymath}u \rightarrow U(x) \mbox{\ as\ } y \rightarrow \infty. \end{displaymath}$

(101)

From the boundary layer equations (4.77) and (4.78) and their derivatives with respect to y, a set of conditions on u can be derived with the aid of the boundary conditions (6.100) and (6.101). These conditions are

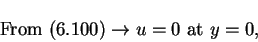$\begin{displaymath}% latex2html id marker 1166 \mbox{From (\ref{eq:ch237b})} \rightarrow u = 0 \mbox{\ at\ } y = 0, \end{displaymath}$

(102)

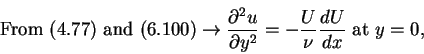$\begin{displaymath}% latex2html id marker 1171 \mbox{From (\ref{eq:ch234b}) and ... ...tial y^{2}} = -\frac{U}{\nu}\frac{dU}{dx} \mbox{\ at\ } y = 0, \end{displaymath}$

(103)

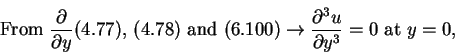$\begin{displaymath}% latex2html id marker 1183 \mbox{From\ } \frac{\partial}{\pa... ... \frac{\partial^{3}u}{\partial y^{3}} = 0 \mbox{\ at\ } y = 0, \end{displaymath}$

(104)

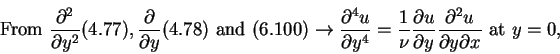$\begin{displaymath}% latex2html id marker 1195 \mbox{From\ } \frac{\partial^{2}}... ...rac{\partial^{2} u}{\partial y\partial x} \mbox{\ at\ } y = 0, \end{displaymath}$

(105)

$\begin{displaymath}\ldots \ldots, \notag \end{displaymath}$

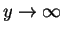and at $y\rightarrow \infty$ we have

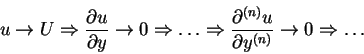$\begin{displaymath}u \rightarrow U \Rightarrow \frac{\partial u}{\partial y} \ri... ...ial^{(n)}u}{\partial y^{(n)}} \rightarrow 0 \Rightarrow \ldots \end{displaymath}$

(106)

In the Pohlhausen's method, and similar approximate methods, a form for the velocity profile u(x,y) is sought which satisfies the momentum equation (6.99) and some of the boundary condition (6.102) to (6.106). It is hoped that this form will approximate to the exact profile, which satisfies all the conditions (6.102) to (6.106) as well as (6.99). The form assumed is

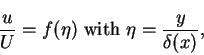$\begin{displaymath}\frac{u}{U} = f(\eta) \mbox{\ with\ } \eta = \frac{y}{\delta(x)}, \end{displaymath}$

(107)

where 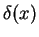$\delta(x)$ is the effective total thickness of the boundary layer. The function 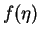$f(\eta)$ may also depend on x through certain coefficients which are chosen so as to satisfy some of the conditions (6.102) to (6.106). Altough strictly the conditions at infinity are only approached asymptotically, it is assumed that these conditions can be transfered from infinity to 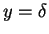$y = \delta$ without appreciable error. Thus equations (6.102) to (6.106) become

f(0) = 0

(108)

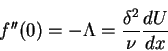$\begin{displaymath}f''(0) = -\Lambda = \frac{\delta^{2}}{\nu}\frac{dU}{dx} \end{displaymath}$

(109)

f'''(0) = 0

(110)

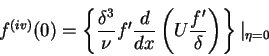$\begin{displaymath}f^{(iv)}(0) = \left\{\frac{\delta^{3}}{\nu}f'\frac{d}{dx}\left(U\frac{f'}{\delta}\right)\right\}\vert _{\eta = 0} \end{displaymath}$

(111)

$\begin{displaymath}\ldots \ldots \notag \end{displaymath}$

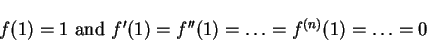$\begin{displaymath}f(1) = 1 \mbox{\ and\ } f'(1) = f''(1) = \ldots = f^{(n)}(1) = \ldots = 0 \end{displaymath}$

(112)

For the assumed velocity profile (6.107), we have that

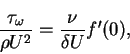$\begin{displaymath}\frac{\tau_{\omega}}{\rho U^{2}} = \frac{\nu}{\delta U}f'(0), \end{displaymath}$

(113)

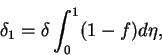$\begin{displaymath}\delta_{1} = \delta\int_{0}^{1}(1-f)d\eta, \end{displaymath}$

(114)

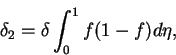$\begin{displaymath}\delta_{2} = \delta\int_{0}^{1}f(1-f)d\eta, \end{displaymath}$

(115)

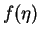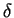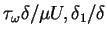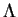If the form assumed for $f(\eta)$ involves m unknown coefficients, these can be specified using m of the boundary conditions (6.108) to (6.112) and the remaining unknown $\delta$ can be determined from the momentum equation (6.99). Also, if only the conditions (6.108), (6.109) and (6.110) are considered, $\tau_{\omega}\delta/\mu U, \delta_{1}/\delta$ and $\delta_{2}/delta$ are functions of $\Lambda$ alone. In this case, substitution of relations (6.113) to (6.115) into (6.99) leads to an equation of the form

$\begin{displaymath}\frac{\nu}{U\delta}f'(0) = \frac{d}{dx}\left\{\delta\int_{0}^... ...ta+\frac{\delta}{U}\frac{dU}{dx}\int_{0}^{1}(1-f)d\eta \notag \end{displaymath}$

$\begin{displaymath}\frac{\nu}{U\delta}f'(0) = \frac{d\delta}{dx}\int_{0}^{1}f(1-... ...\int_{0}^{1}f(1-f)d\eta+\int_{0}^{1}(1-f)d\eta\right\} \notag \end{displaymath}$

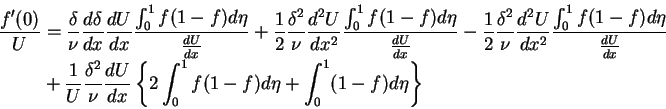$\begin{displaymath}\begin{split} \frac{f'(0)}{U} & = \frac{\delta}{\nu}\frac{d\d... ...t_{0}^{1}f(1-f)d\eta+\int_{0}^{1}(1-f)d\eta\right\} \end{split}\end{displaymath}$

(116)

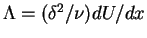Since $\Lambda = (\delta^{2}/\nu)dU/dx$ , we can write the equation above in the form

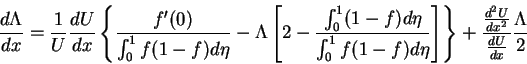$\begin{displaymath}\frac{d\Lambda}{dx} = \frac{1}{U}\frac{dU}{dx}\left\{\frac{f'... ...}+\frac{\frac{d^{2}U}{dx^{2}}}{\frac{dU}{dx}}\frac{\Lambda}{2} \end{displaymath}$

(117)

or simply

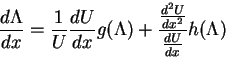$\begin{displaymath}\frac{d\Lambda}{dx} = \frac{1}{U}\frac{dU}{dx}g(\Lambda)+\frac{\frac{d^{2}U}{dx^{2}}}{\frac{dU}{dx}}h(\Lambda) \end{displaymath}$

(118)

where

$\begin{displaymath}g(\Lambda) = \left\{\frac{f'(0)}{\int_{0}^{1}f(1-f)d\eta}-\La... ...int_{0}^{1}(1-f)d\eta}{\int_{0}^{1}f(1-f)d\eta}\right]\right\} \end{displaymath}$

(119)

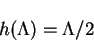$\begin{displaymath}h(\Lambda) = \Lambda/2 \end{displaymath}$

(120)

Pohlhausen used a family of velocity profiles given by the quartic polynomial

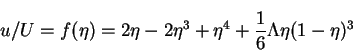$\begin{displaymath}u/U = f(\eta) = 2\eta-2\eta^{3}+\eta^{4}+\frac{1}{6}\Lambda\eta(1-\eta)^{3} \end{displaymath}$

(121)

chosen to satisfy the boundary conditions

$\begin{displaymath}f(0) = 0, f''(0) = -\Lambda, f(1) = 1, f'(1) = f''(1) = 0 \notag \end{displaymath}$

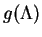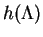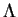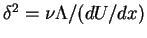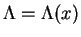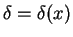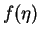With the chosen velocity profile (6.121), we can evaluate the functions $g(\Lambda)$ and $h(\Lambda)$ , and then integrate numerically equation (6.118) to obtain $\Lambda$ as a function of x and through equation $\delta^{2} = \nu\Lambda/(dU/dx)$ . By the substitution of $\Lambda = \Lambda(x)$ and $\delta = \delta(x)$ in the assumed velocity profile $f(\eta)$ , we obtain the velocity profile for any x and y.

Next: Stagnation Point flow. Up: No Title Previous: Energy Integral.

Karl P Burr
2003-03-12