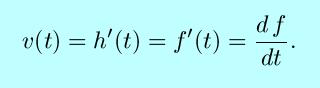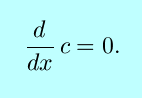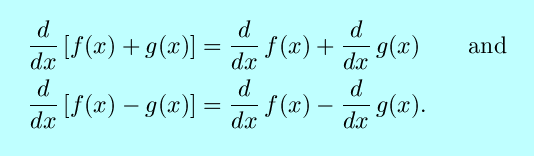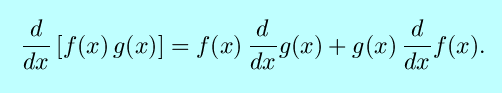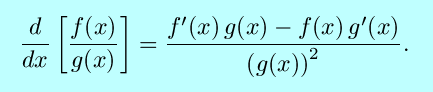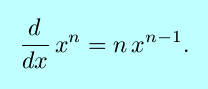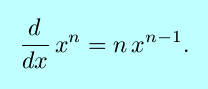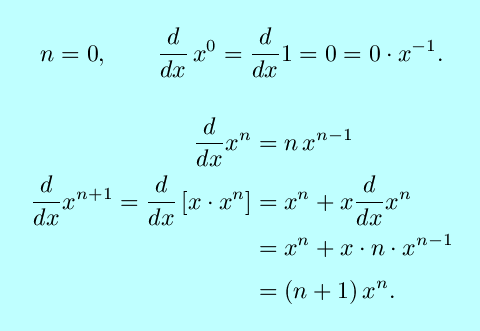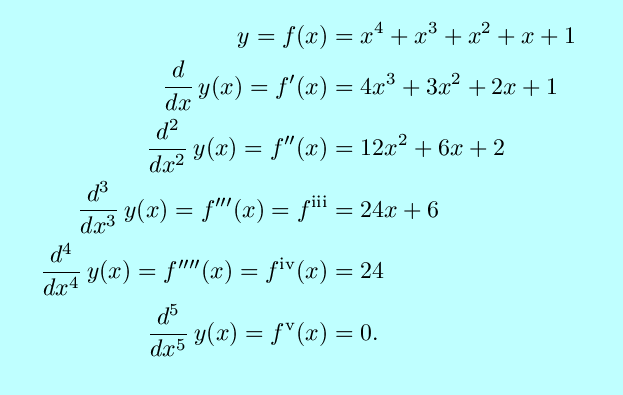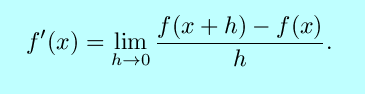Unit 2: The Derivative
Unit 2: The Derivative
Much of the work we are going to do in this course consists of taking
one or more functions, and producing a new function. The first of
these methods is differentiation: we take a function, call it
f(x) for convenience, and produce a new function which we call the
derivative of f(x).
We have several notations
for this process. (In fact, we
probably have too many notations. Such is mathematics.) If we again
denote our function by f(x), its derivative can be denoted by
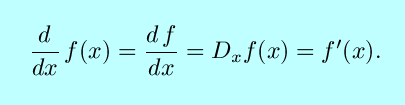 If we express our function in the x-y plane
as y=f(x), then we gain the notations
If we express our function in the x-y plane
as y=f(x), then we gain the notations
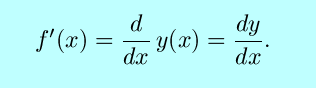 There is, of course, a reason we want the derivative of a function.
The derivative is the slope of the original function at any
given point. This will be explained in the reading along with pretty
pictures of tangent lines. The method used to define the tangent is to
approach the tangent line through a sequence of secants; again, refer
to pictures in the various texts. Following the secant lines, we
arrive at our definition of the derivative:
There is, of course, a reason we want the derivative of a function.
The derivative is the slope of the original function at any
given point. This will be explained in the reading along with pretty
pictures of tangent lines. The method used to define the tangent is to
approach the tangent line through a sequence of secants; again, refer
to pictures in the various texts. Following the secant lines, we
arrive at our definition of the derivative:
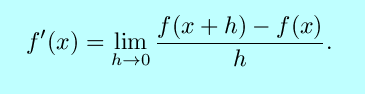 (Sometimes
(Sometimes 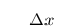 , ``Delta -x'', is used instead of
h. The triangle symbol is the Greek letter "Delta".)
, ``Delta -x'', is used instead of
h. The triangle symbol is the Greek letter "Delta".)
This definition raises several interesting questions: what
is this limit? (This problem was brushed off for a few
centuries. Its eventual answer forms the subject material of
analysis.) How do we know it exists? (Sometimes it doesn't. See
discussion of |x| in the text.). We follow a long tradition
of beginning calculus courses in firmly brushing these questions under
the rug. In most of the cases of interest, we are dealing with a
``smooth'' function where we may take the derivative with impunity.
There is another interpretation of the derivative that you should also
understand: the derivative indicates the rate of change of
the original function. This interpretation is especially important
when the function is expressed in terms of time. For example we may
have the height of a rocket expressed as h =
f(t), giving the height for every
instant. The upward component of the velocity of the rocket,
i.e., the rate of change of the height, is given by
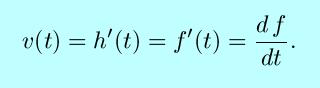 Become accustomed to this idea now; you will see
it again and again.
Become accustomed to this idea now; you will see
it again and again.
Now that we've developed a feel for the derivative, we need
method for calculating the derivative without applying the definition
over and over again. Using the definiton, the following rules of
differentiation can be derived. You should make sure to go over the
derivation of these rules:
- The constant rule: if c is a
constant, then
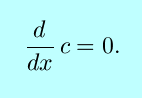
- The sum and difference rules:
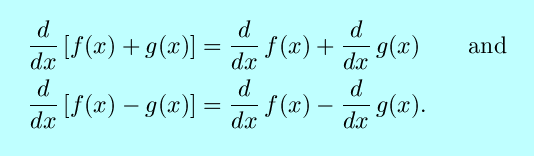
- The product
rule:
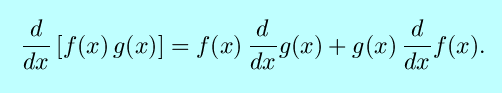
- The quotient
rule:
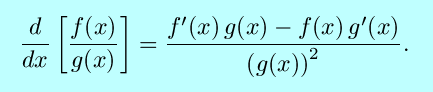
- The power
rule
(first version):
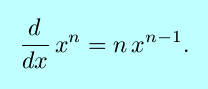
Note that this is only the first version of the power rule; we will
generalize this rule in the next unit, when we have the chain
rule. The proofs of the various rules follow from the definition of
the derivative and some algebraic manipulation. You should be able to
follow the proofs, but you needn't worry about reproducing them. The
power rule is an interesting case in that it can be proven using
induction for positive integral powers.
(The following discussion will be extended when the World Wide Math
Integer Arithmetic page is completed.)
To over-generalize madly, induction arguments can come up whenever the
natural numbers are involved in a formula. Both texts have further
examples of induction proofs in their respective appendices. While
induction proofs aren't vital to your understanding of calculus, they
are a piece of mathematical culture you should learn. The general form
is to prove a base case, either n = 0 or
n = 1 or wherever you want to start: for the
case of the power rule,
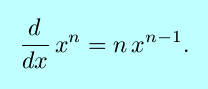 Next is the inductive step: assume that the proposition is true
for all values less than n, then prove it for n+1:
Next is the inductive step: assume that the proposition is true
for all values less than n, then prove it for n+1:
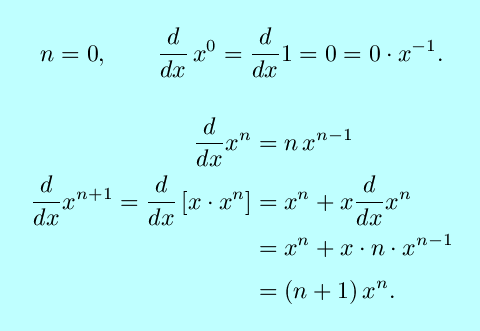 Note that the product rule was used in the above.
Mastering these rules for differentiation is important; work enough
practice problems so
that you can differentiate blindfolded!!
Note that the product rule was used in the above.
Mastering these rules for differentiation is important; work enough
practice problems so
that you can differentiate blindfolded!!
Now is a convenient time as any to mention that you can take
derivatives multiples times. The derivative of a function is a
perfectly good function in its own right: it can be graphed, and one
can ask for its slope at any point. Relative to the function we
started with, this is a second order derivative. We, of course,
have lots of fun notation for this notion, and for the obvious next
steps:
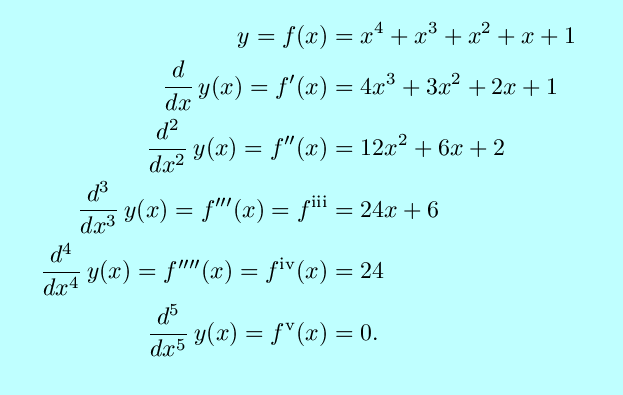
Objectives:
After completing this unit you should be able to:
- Understand the derivative as expressing the slope of a curve at
each point on the curve.
- Understand the derivative as expressing a rate of change.
- Be able to use
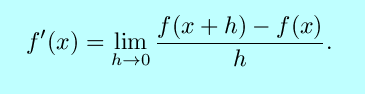 to set up derivatives, and to calculate derivatives in some cases.
to set up derivatives, and to calculate derivatives in some cases.
- Derive the rules of differentiation.
- Calculate the derivative of any rational function.
- Calculate higer order derivatives.
Suggested Procedure:
- Read Simmons, first edition chapter 2 and sections 3.1, 3.2, and
3.5, or
- Read Simmons, second edition chapter 2 and sections 3.1, 3.2, and
3.6.
- Read the following World Web Math Pages:
- Do some problems in Simmons
- 2.2 : # 1, 3, 5, 7, 8
- 2.3 : # 1, 4, 12
- 2.4 : # 1, 4, 8, 10, 11
- 3.1 : # 1, 9 - 12
- 3.2 : # 1, 2, 5, 7, 8, 9
- Take the Practice Unit
Test, Xdvi or PDF
- Ask your instructor for a unit test.
Independent Study Page |
Calculus Page |
World Web Math CategoriesPage
watko@mit.edu
Last modifed February 15, 2002
 Unit 2: The Derivative
Unit 2: The Derivative Unit 2: The Derivative
Unit 2: The Derivative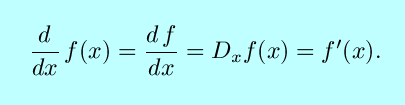
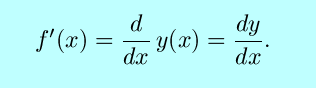
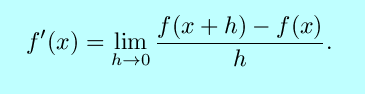
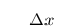 , ``Delta -x'', is used instead of
h. The triangle symbol is the Greek letter "Delta".)
, ``Delta -x'', is used instead of
h. The triangle symbol is the Greek letter "Delta".)