Complex networks and collective behavior in nature

Modeling animal behaviour

Computers can be used to simulate animal behaviour by indicating a set of rules through which particles (animals) interact to each other. Pretty much these interactions account for the attraction and/or repulsion between them. Within these rules is also needed a mathematical description of position and velocity for each particle in the sytem. An important parameter to consider is the range of the interactions to take in count. In the most simple case researchers define a circular or spherical area in which each particle interact within the particles that are in the defined area or volumen. By varying these parameters, it has been shown, that particles adopt different orientations. In the following figure taken (without permission)from an article in the New York times (Zimmer, C., NYT, 2007) we can see the different patterns obtained as varying the interaction rules.

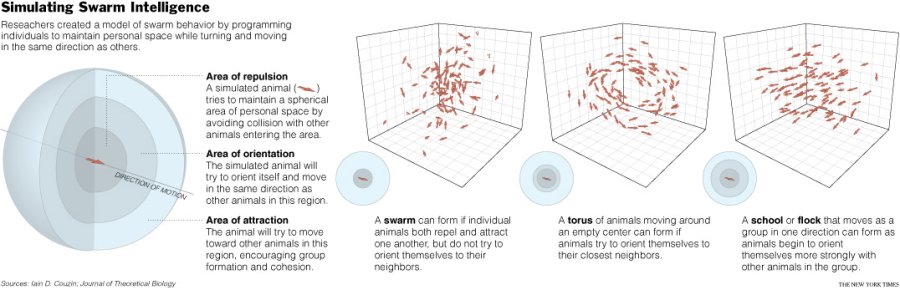
Vicsek Model of self-propelled particles

The central idea in Vicsek's model is that every step in time, each particle moves in the average direction of motion of its neighbors, plus some noise. In other words, each particles is following its neighbors. But the particles make "mistakes" when evaluating the direction of motion of their neighbors, those mistakes are considered the noise. There are several sources of noises, but it can be divided into two groups:

Extrinsic noise. Such as the environment. Each particle do not see very well the direction in which their neighbors are moving. We call this extrinsic noise because it has to do with uncertainties in the particle-particle "comunication" mechanism

Intrinsic noise. Is is possible to imagine that particles as having some kind of "free will"m si that even when they know the direction of their neighbors, they "decide" to move in a different direction. Is is call intrinsic noise, because it has to be with the internal decsision-making mechanism of the particles.

In the original work, Vicsek and collaborators used just intrinsic noise and showed that, when the noise magnitud increases, the system undergoes a phase transition from ordered state where all the particles move in the same direction, to a disordered phase where the particles move in random uncorrelated directions.

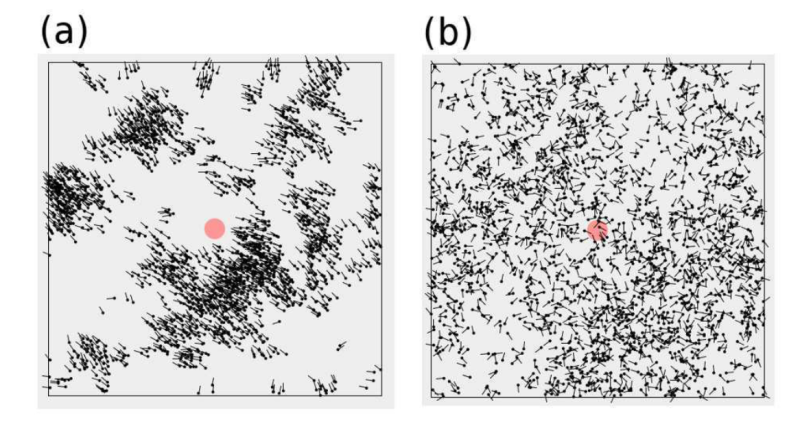
Snapshots of the Vicsek model (Taken from ref [4] with permission from the author) a) For small noise ( $\eta$ = 0.1), all the particles move in the same direction. b) For large noise ( $\eta$ = 0.8), the particles move in random uncorrelated directions.The red circle at the center indicates the size of the interaction among neighbors used for numerical simulations.

The Vicsek Model. Mathematical details

The model consists of $N$ particles placed on a two-dimensional square box of sides $L$ , with periodc boundary conditions, which are a set of conditions used to simulate a large system by modelling a small part that is far from its edge. That consider that an object wich leaves the simullation cell on one side enter back on the other.

Each particle is characterized by its position $x_n(t)$ , and its velocity $v_n(t)=v_{0}e^{i\theta_{n}(t)}$ , which is represented as a complex number to emphasize the velocity angle $\theta_{n}(t)$ . All the particles move with the same speed $v_{0}$ . What changes from one particle to another is the direction of motion given by the angle $\theta_{n}(t)$ .

In order to state mathematically the interaction rules between the particles, we can define $U_{n}(r_{0};t)$ as the circular neighborhood with radius $r_{0}$ centered at $x_n(t)$ , and $k_n(t)$ the number of particles within this neighborhood. Let $V_n(t)$ be the average velocity of the particles withing each neighborhood (circle) $U_{n}(r_{0};t)$ :

$V_{n}(t)=\frac{1}{k_{n}(t)}\sum_{{j:x_{j}\in U_n}}v_{j}(t)$
The last formula is just the sum of the velocities of each particle in the neighborhood divided by the number of particles in that neighborhood. With these definitions, the interaction between the particles with intrinsic noise is given by ythe simultaneous updating of all the velocity angles and all the particles positions according to the rules

$\theta_{n}(t+\Delta t )=Angle[V_{n}(t)]+\eta \xi _{n}(t)$
$v_{n}(t+\Delta t )=v_{0}e^{i\theta_{n}(t+\Delta t)$
$x_{n}(t+\Delta t )=x_{n}(t)+v_{n}(t+\Delta t)\Delta t$

Where $\xi _{n}(t)$ is a random variable uniformly distributed in the interval [-pi,pi], and $\eta$ is the noise intensity, which is a positive parameter.

Analogously, the interaction rule with extrinsic noise is given by

$\theta_{n}(t+\Delta t )=Angle[V_{n}(t)+\eta e^{i\xi _{n}(t)}]$
$v_{n}(t+\Delta t )=v_{0}e^{i\theta_{n}(t+\Delta t)$
$x_{n}(t+\Delta t )=x_{n}(t)+v_{n}(t+\Delta t)\Delta t$

The equations may look scary, but we just should note that in the first set of equations (intrinsic noise) the angle of the average velocity is computed and then a scalar noise is added to this angles, whereas in the extrinsic noise case, a random vector is added to the average velocity and then the angle of the resultant is computed. We can interpret the average velocity $V_n(t)$ , as the signal that the n-th particle receive from its neighborhood, and the Angle function as the particle's decision-making mechanism. Therefore in the set of equations for the intrinsic noise case, the particle clearly receives the signal from its neighborhood, computes the angle of motionm but then decides to move in a different direction. In contrast, for the extrinsic noise case, the particle receives a noisy signal from the neighborhood, but once the signal has been received, the particle computed the angle from the perceived signal, and follows it.

At any time, the amount of order in the system is measured by the instantaneous order parameter, that is defined as the absolute value of the sum of all the particle velocities in the system, divided by the total number of particles multipled by the speed.

$\psi _{\eta}(t) = \frac{1}{Nv_{0}}\left | \sum_{n=1}^{N}v_{n}(t) \right |$

Where the subscript $\eta$ indicate that the order parameter in the system depends on the noise intensity. After a transient time, the system reaches a steady state, and we can average the order parameter $\psi _{\eta}(t)$ over different simulations with the same noise, or equivalently over time. The stationary order parameter $\psi (\eta)$ is defined as

$\psi (\eta) = \lim_{t \to \infty }\left \langle \psi _{\eta}(t) \right \rangle = \lim_{T \to \infty}\frac{1}{T}\int_{0}^{T}\psi _{\eta}(t)dt$

Where in the brakets in the first expression denotes the average over realizations (different simulations with the same noise), whereas the average over time is given by the integral. The next figure shows a typical phase transition curves for both types of noise, intrinsic and extrinsic.

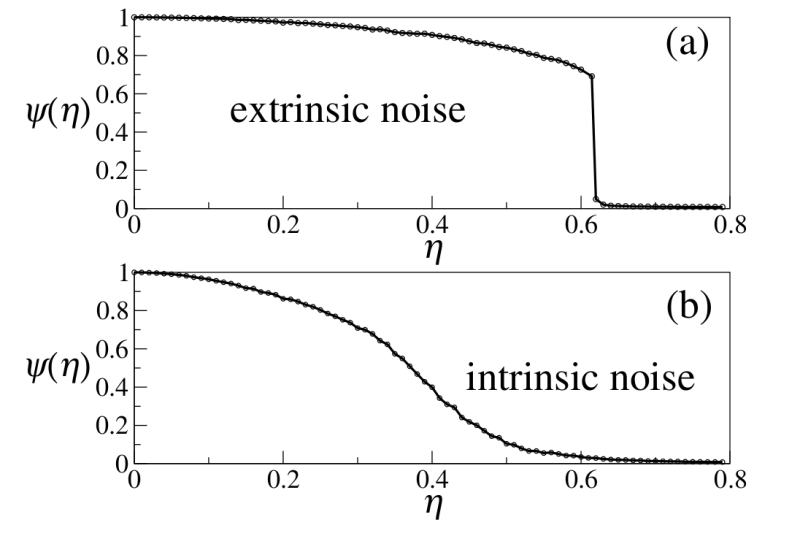
Phase transition diagrams for a system with a) extrinsic noise and b) intrinsec noise (Taken from [4] with permission from the author).

The discontinous character of the phase transition ofr the extrinsic noise case is evident (top figure). As far as we can tell, there are no doubts that the phase transition is discontinuos in this case, and there is plenty of numerical and theoretical evidence supporting this finding. In contrast, the phase transition for the intrinsic case is still under debate. Determining the nature of the phase transition in the Vicksek model with intrinsic noise is important, among other things, for understanding the physical principles through wich collective order emerges in swarms and flocks, and more generally, in systems aout of equilibrium.

Back