Complex networks and collective behavior in nature

Studying Complex Networks^[2]

The study of networks pervades all of science, from neurobiology to statistical physics. The most general study of complex networks can be divided in two different but complementary fields. structure and dynamics, in the former, the interest is focused on the topological network's properties, such as description tell us how the nodes are connected. How does one characterize the wiring diagram of a food chain or the internet or the metabolic network of the bacterium Escherichia coli? Are there unifying principles underlying their topolgy? . Some of the most important properties that determine the structure (or topology) of a network are the followings

The degree distribution (or neighbour distibution) $P(k)$ : Is the probability that a randomly chosen node has $k$ connections (or neighbours). For example, in networks of sexual partners, $P(k)$ is the probability that one randomly chosen person in a society had had $k$ different sexual partners along his or her life
Aggregation coefficient $C$ : Is the probablity that two directly connected nodes to a third node, are connected to each other. For example in a network of friends, is the probability that two of my friends are also friends to each other.
The minimum length $L_{ij}$ between two nodes $v_{i}$ and $v_{j}$ : Is the minimum number of steps to reach one node $v_{i}$ from a node $v_{j}$
The average length in the network $L$ : Is the average of the minimum length $L_{ij}$ between all the possible pairs of nodes $(v_i,v_j)$ in the network.
The island size distribution $P(s)$ : Is the probability of an island of being composed by $s$ nodes
The size of the bigest island, that is denoted by $S_{\infty }$

As an example of the above concepts lets analyze the following figure.

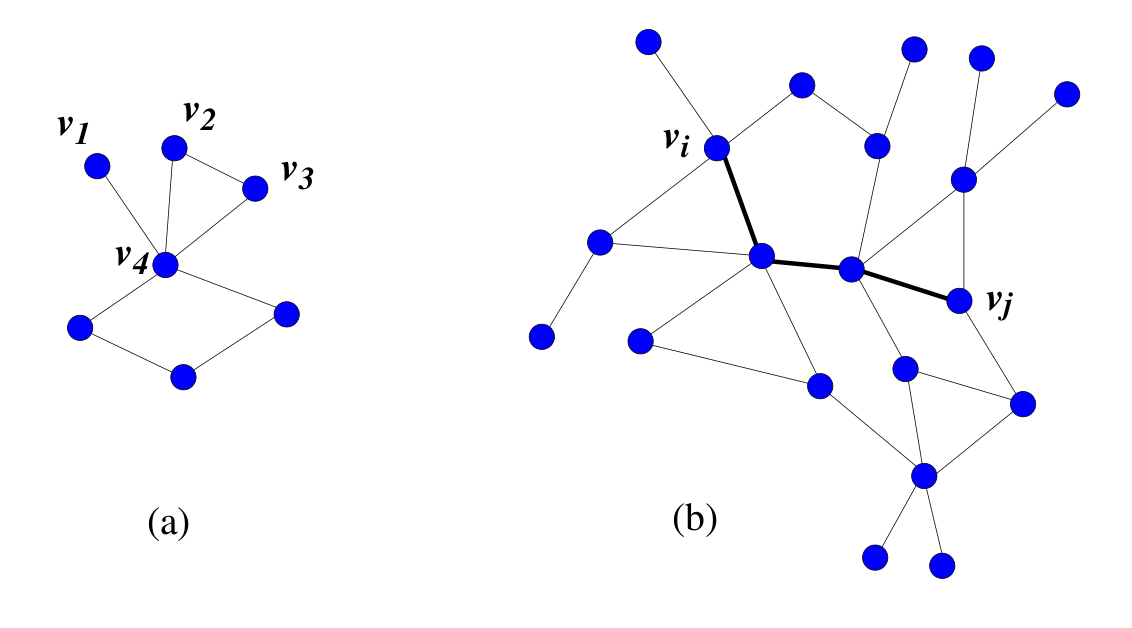
In a ) The nodes $v_{1}$ , $v_{2}$ and $v_{3}$ are connected to the node $v_{4}$ . However, the node $v_{1}$ and $v_{2}$ are not connected to each other, whereas the nodes $v_{2}$ and $v_{3}$ are connected. If this were a friendship network, that means not all the friends of $v_{4}$ are friends among them, which reduce the aggregation coefficient. b) Eventhough there are many paths to go from $v_{i}$ to $v_{j}$ , the minimum length path is composed by 3 steps, indicated by the bold lines.

Structure of complex networks. Degree distribution

The most important propertie that characterize a network structure is the degree distribution (neighbor distribution) $P(k)$ . In the recent studies that classify complex networks, it has been found that there are three main kinds of distributions, defining three different structures or topologies.

Poisson topology	$P(k)=e^{-z}\frac{z^{k}}{k!}$
Exponential topology	$P(k) = Ce^{-\alpha k}$
Scale-free topology	$P(k) = Ck^{-\gamma}$

The networks with Poisson topology are important due to historical reasons, those were the first networks mathematically analized. That analysis was carried out by the hungarian mathematicians Paul Erdos (1913 - 1996) and Alfred Renyi (1921 - 1970) during the 1950's decade. They also reported the first phase transition in networks with Poisson topology. These networks are also know as Erdos-Renyi networks. However, although their historical importance, networks with Poisson topology are far from being a realistic representation of networks present in nature. In 1998 started the systematic study of real complex networks, in this study participated mainly and independently Albert Laslo-Barabasi, Ricard Sole and Mark J. Newman. They found that expnoential topology can describe some real networks. But their most outstanding result was that scale-free networks are present almost everywhere, including metaboic networks within a cell (in E. Coli $\gamma_i = 2.2$ ), the number of domains in the WWW can be described by $\gamma_i = 1.9$ and the number of citations in the Journal Phys. Rev. D by $\gamma_i = 2.3$ . Something to remember, is that the scale-free property is common but not universal, examples of other structures are the coauthorship networks of scientists, $P(k)$ that is fit better by a power law with an exponential cutoff, the power grid of the western United States, $P(k)$ follows an exponential distribution and a social network of Mormons in Utah, $P(k)$ is gaussian. Nevertheless, the scale-free case has stimulated a great deal of theorizing.

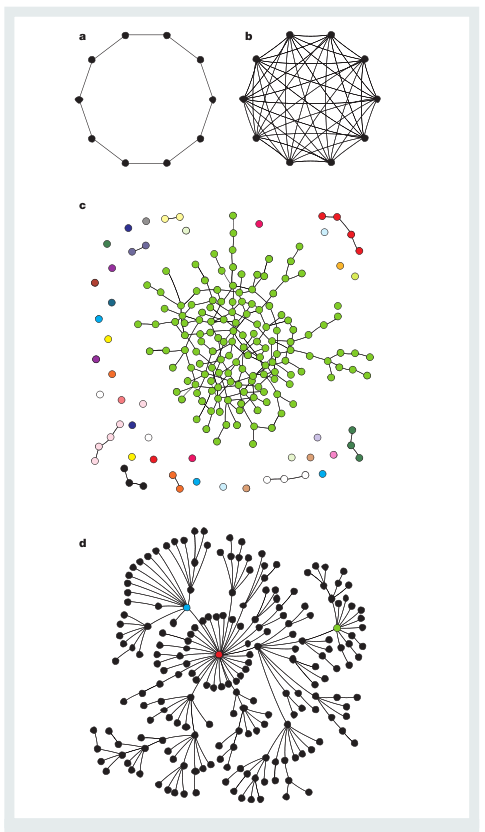a) Ring of ten nodes connected to their nearest neighbours. b) Fully connected network of ten nodes. c) Random graph constructed by placing n nodes on a plane, then joining pairs of them together at random until m links are used. Nodes may be chosen more than once, or not at all. The resulting diagram would be a snarl of cross-crossed lines. To clarify it, the author of the image segregated the different connected components, coloured them, and eliminated as many spurious crossing as possible. The degree, or number of neighbours, is Poisson distributed across the nodes. d) Scale-free graph, grown by attaching new nodes at random to previously existing nodes. Notice the existence of hubs (nodes with accumulation of connections), because the probability of attachment is proportional to the degree of the target node; thus richly connected nodes tend to get richer. Figure taken without permission from Strogatz S. H., Exploring complex networks, Nature (2001), 410 268 - 276

Back Next

Studying Complex Networks[2]

Structure of complex networks. Degree distribution

Studying Complex Networks^[2]