Complex networks and collective behavior in nature

The giant island

Lets go back to the buttons model described before. Initially we had all the buttons disconnected to each other on the table, but as soon as we start attaching button pairs, we start forming islands of connected buttons. At the begining the islands are small, but the more we add connections, the bigger the islands are. Eventually a giant island will be formed. An island that is much larger than any other island.

The size of the giant island is important to study for example spread of diseases in a society, where instead of attached buttons we had people spreading the disease to each other. The islands are the groups of people that are infected and the disease turns into an epidemia when a giant island is formed, in which almost all the society is involved.

The question that we want to solve is: Given a set of conditions, how many connections (contagious) have to be stablished in order to form a giant island?. The last question was solved by Erdos and Renyi, who where the first into show the existence of a phase transition in networks theory. That transition is precisely the formation of a giant island. Although their original work was done with Poisson networks, is not difficult to generalize the concept to networks having any topology.

To calculate the size of the giant island, we can start considering $q$ as the probability that a randomly chosen node $v_i$ does not belong to the giant island. Lets supose that $v_i$ has $k$ neighbors. Clearly $v_i$ does not belong to the giant island if and only if none of its neighbors does not belong to the giant island too. Furthermore, the probability, $q$ should satisfy the following equation.

$q=\sum_{k}P(k)q^{k}$

The left hand side of the equation is simply the probability $q$ that $v_i$ does not belong to the giant island. The right hand side is the probability $P(k)$ that $v_{i}$ had $k$ neighbors, multiplied by the probability $q^{k}$ that none of them of its $k$ neighbors belong to the island. The sum over $k$ considers all the possible neighbors that $v_{i}$ could have and in this case $k$ goes to infinity. In the case where $P(k)$ is a Poisson distribution, the expression for $q$ turns into

$q=\sum_{k=0}^{\infty}e^{-z}\frac{(zq)^{k}}{k!}=e^{z(q-1)$ Now, lets denote as $p=1-e^{-z}$ to the probability that an arbitrary node belongs to the giant island, then we have

$p=1-e^{-zp}$ The last is a transcendental equation, meaning that can not be solved analitically. However it can be solved numerically to find $p$ for each value of $z$ . The following figure shows $p$ as a function of $z$ . Note that for $z<1$ , the probability of belong to the giant island is zero. In other words, there is no giant island for $z<1$ . As z increases (equivalent to increasing the number of connections in the network), the island increases and at $z=1$ the giant island appears. This is an interesting result, in average is just necessary one connection per node to lead the formation of the giant island. If we keep increasing the value of $z$ , the size of the giant island increases more and more. The figure resembles the characteristic phase transition of second order at $z=1$ .

In conclusion,as $M$ increases, the islands grow, at first by linking to isolated nodes and later by coalescing, with other islands. A phase transition occurs at $z=1$ or $M=\frac{N}{2}$ , where many islands crosslink spontaneously to form a single giant component.

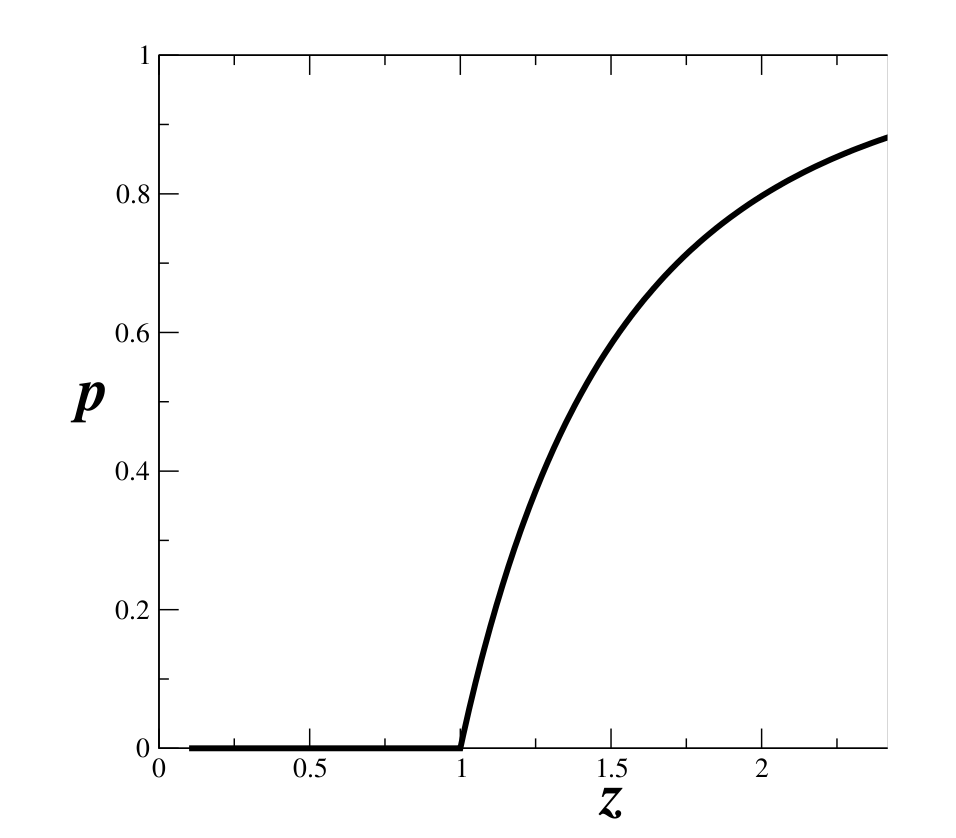
Probability $p$ of belonging to the giant island as a function of the average connectivty $z$ in the network, considering Poisson topology.

For free-scale networks, the derivation is not shown, but the giant component always exists and the probabilitty of belonging to that is p = 1. This interesting result is a consequence of the existence of highly connected elements. Those elements keep all the network connected avoiding formation of small islands. The above results have important implications for example in spread of diseases in a society. In networks with Poisson topology there is always the possibility of vaccination of enough number of people in order to keep the average connectivity in the network below 1. In such as case, we could stop the epidemy, because there is no giant island.

On the other hand if the network presents free-scale topology, there is always a giant island and the probabiloty of belonging to that is p = 1. Then the only way to stop the spread od the disease if through vaccination of all the people in the society.

Back Next