For the case in wich any of the existing node can be selected with the same probability to be connected with the new added node, the probability
)
in independent of 
and is given by the following expression
=\frac{1}{N(t)}=\frac{1}{t+1})
Where =t+1})
is the nodes total number at time 
. After long enough time the function )
reaches a steady state in which =P(k,t)=P(k))
. In that steady state the solution for the time evolution is
=2^{-k})
which is the exponential distribution. It is important to mention that this distribution emerges in the context of networks growth as a result of having equal probability of any existing node of being selected to form a new connection, with the recently added node.
In many networks in real life, connections are not formed based on equivalent probabiliies of being selected. For this reason, Barabasi introduced the concept of preferential attachment, in which the new nodes are added to the network with some bias. Networks following this principle present, few hubs that have lots of connections, while anyother else only has few.
Barabasi suggested that the probability of connection should take the following form:
=\left ( \sum_{n=0}^{N(t)}k_{n} \right )^{-1}k)
where 
is the n-th node connectivity existing at time 
. The factor before is just to guarantee that the probability is normalized. With this expression, the behaviour is as follows: the larger the connectivity, the larger the probability of form a connection with it.
Due to the fact that nodes are added in each time step, if we start with zero conecctions at time 
then for any time
we have
}k_{n}=2t)
and furthermore,
=\frac{k}{2t})
In the limit of
, the system reaches a steady state and then the stationary connection distribution
)
can be expressed as follows
=\frac{4}{k(k+1)(k+2)})
Although , the above expression is not a perfect power law (figure at the bottom), for high values of k, the distribution behaves as
\sim k^{-3})
. This result is very interesting because, the preferencial attachment leads to connectivity distributions that have free-scale tails. These tails are responsible of generating elements highly connected. On the other hand the result is also discouraging because the preferencial attachment process allways gives us the exponent
, which is not frequently found in
nature. In other words, eventhougth the preferential attachment behaviour gives us a power law, is it unable of accurately describe the variety of exponents found in nature. For this reason, there have been many proposals for the probability function
to describe different preferential attachments.
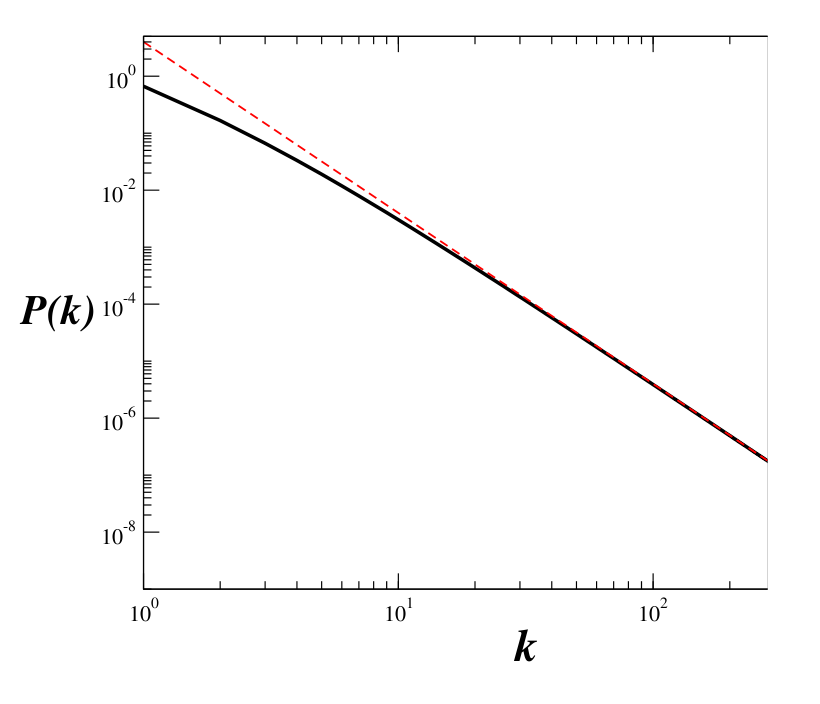
Log-Log plot of connections distribution for free-scale topology The red dashed line is a power law plot =4k^{-3})
, we should note that \sim 4k^{-3})
for high values of
Back Next