Quantitative Microscopy and Tomography of Live Cells

Synthetic Aperture Tomography
Synthetic aperture tomography is a technique to synthesize an object from a series of images taken while moving a source or a detector. According to Huygens’ principle, any directional plane wave can be created from a set of position-dependent focused beams. By measuring the phase and amplitude of a focused beam with a sample translating across the beam, plane waves with any incident directions can be synthesized. From a set of angular phase images of synthesized plane waves, a 3D image can be constructed using a filtered back projection algorithm. This source translation technique, referred to as synthetic aperture tomographic phase microscopy (sTPM), was first suggested by Nahamoo et al [10] for ultrasound imaging, but has never been before implemented in the optical regime. Recently, moving a sample across a line-focused laser beam and using the plane wave synthesis technique, we have shown 3-D refractive index map of the sample can be obtained [2].

Figure 1 shows the experimental set-up. The E-field measurement is based on a heterodyne Mach-Zehnder interferometer [3]. The output of a HeNe laser (20 mw, λ = 632.8nm from Melles Griot, USA) is split by an optical beam splitter (not shown). One beam (the object beam, shown in red) travels through an object located on the sample stage of an inverted microscope (Axiovert S100, Zeiss Germany). With the use of a cylindrical lens, the optical system is presented in two orthogonal axes: an imaging axis (Fig. 1(a)) with a plane wave illumination and a Fourier axis (Fig. 1(b)) with a focused beam illumination. The reference beam, a planar beam whose frequency is shifted by 1.25kHz using two acousto-optic modulators is brought to interfere with the expanded focused beam at a fast CMOS camera (M2; Fastcam 1024PCI, Photron Japan). The camera records four interferometric images at 5kHz frame rate [3,4].

Figure 1(c) is a typical bright field image of a 10 μm polystyrene bead measured at M1. Figure 1(d) shows the line-focused beam illuminating the center of the same bead in (c), with the C1 in position. Typical interferometric images taken are shown in Fig. 1(e), when line focus beam is positioned about the center of a 10 μm bead. By applying a four-frame phase shifting interferometry (4f-PSI) algorithm [5], the phase image is obtained (Fig. 1(f)).

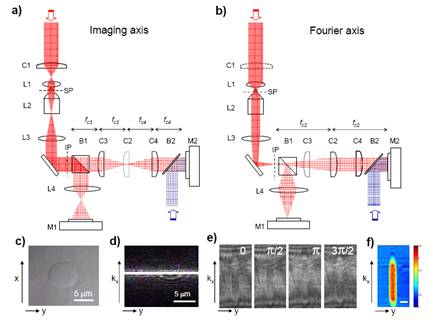
Figure 1. Experimental set-up. Two views depend on the axes of cylindrical lenses are shown: (a) Imaging axis in which the illumination beam is a plane wave, (b) Fourier axis in which the illumination is a focused beam. (c) Bright field image of a 10μm polystyrene bead. (d) Line focus beam through a bead imaged at camera M1. (e) Four consecutive π/2 phase-shifted interferometric images of the bead imaged at camera M2. (f) Quantitative phase image of the bead processed from (e).

Figures 2(a)-(c) depict the x-y slices of the reconstructed tomogram of a HeLa cell with an axial distance of two microns between each slice image. Detailed structures such as nucleolus and nucleus are clearly visible, especially in Fig 2(b). A bright field image at approximately same focus has been taken (Fig. 2(d)) to show the close correspondence with the tomogram.

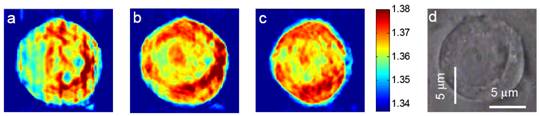
Figure 2. Refractive index tomogram of a live HeLa cell obtained using the experimental set-up in Fig. 1. (a) – (c) Lateral slices of tomogram images for a HeLa cell in 2 μm steps from top to bottom. (d) Bright field image of the same HeLa cell. Color bar indicates refractive index at λ = 632.8 nm.

To summarize, the proof of concept for the synthetic aperture tomography was successfully demonstrated in the optical regime for a sample in translational motion. We are trying to apply it to a sample in a microfluidic channel, in which defocus and rotation of the sample are expected. The synthetic aperture tomography is capable of obtaining the refractive index map of a moving sample, so it can be potentially incorporated into flow cytometry, and can thus enable rapid data acquisition for a large number of cells.

1. D. Nahamoo, S. X. Pan, and A. C. Kak, “Synthetic aperture diffraction tomography and its interpolation-free computer implementation,” IEEE Transactions on Sonics and Ultrasonics,
   Vol. SU-31, July 1984, pp. 218-229.
2. Niyom Lue, Wonshik Choi, Gabriel Popescu, Kamran Badizadegan, Ramachandra R. Dasari, and Michael S. Feld, "Synthetic aperture tomographic phase microscopy for 3D imaging of live cells in translational motion," Opt. Express 16, 16240-16246 (2008).
3. C. Fang-Yen, S. Oh, Y. Park, W. Choi, S. Song, H. S. Seung, R. R. Dasari, and M. S. Feld, “Imaging voltage-dependent cell motions with heterodyne Mach-Zehnder phase microscopy,” Opt. Lett. 32, 1572-1574 (2007).
4. W. Choi, C. Fang-Yen, K. Badizadegan, S. Oh, N. Lue, R. R. Dasari, and M. S. Feld, “Tomographic phase microscopy,” Nature Methods 4, 717-719 (2007).
5. X. Zhong, “A four-frame phase shift method insensitive to phase shifter nonlinearity,” J. Opt. A: Pure Appl. Opt. 8, 300-303 (2006).