Lab 5
9.59 Lab in Psycholinguistics
library(tidyverse)Multiple comparisons
One thing that’s come up recently in the literature is the issue of multiple comparisons. Here’s a way researchers sometimes plan studies: I want to see if group A differs from group B in cognitive ability X, but I don’t know exactly how to measure X. I’ll collect response time, and accuracy, and time spent on response, and also, since none of those might work out, I’ll collect some measures of IQ and favorite dog breed. Then I’ll see which of those yields significant differences!
Do you see the problem here?
We know that you can get p-values < 0.05 when the null hypothesis is true, so what happens when we run lots of tests?
experiment <- function() {
sample1 <- rnorm(50, 20, 10)
sample2 <- rnorm(50, 20, 10)
p_value <- t.test(sample1, sample2)$p.value
return(p_value)
}
tests <- function(num_test) {
p_values <- replicate(num_test, experiment())
num_sig <- sum(p_values < 0.05)
return(num_sig)
}
mult_comp <- data_frame(num_test = 1:100) %>%
mutate(num_sig = map_dbl(num_test, tests))
ggplot(mult_comp, aes(x = num_test, y = num_sig)) +
geom_point() +
geom_smooth(method = "lm")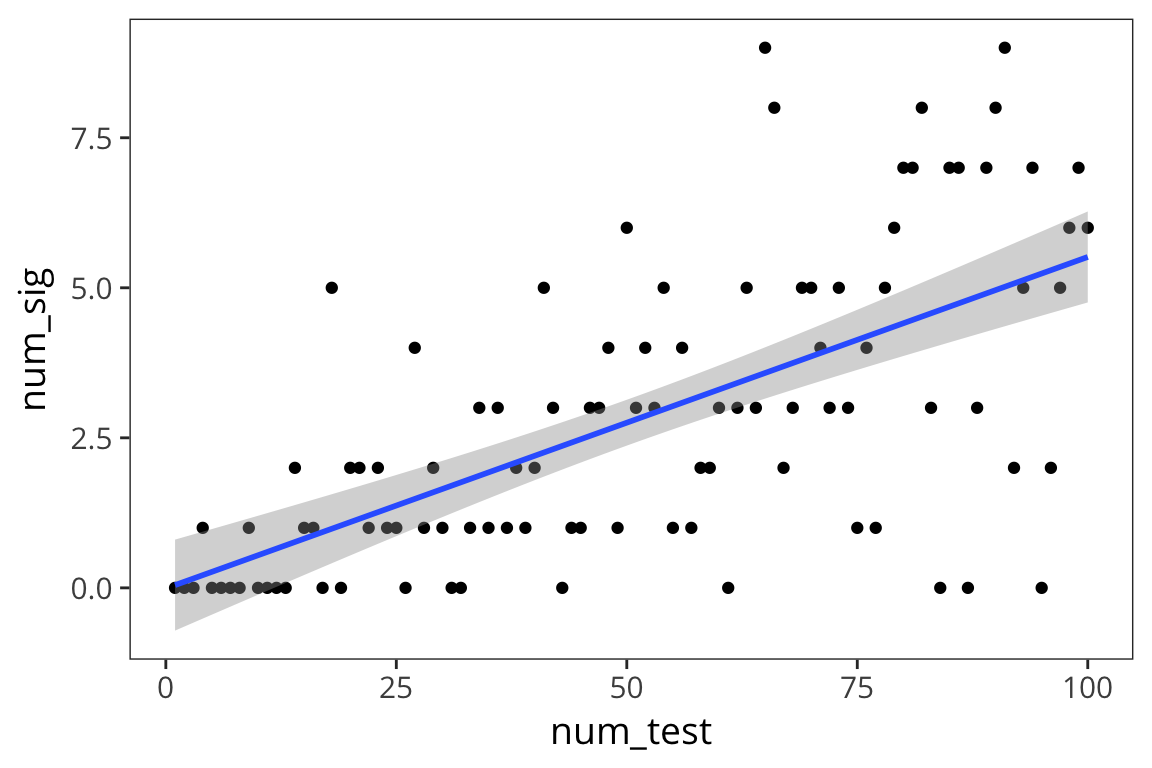
As you can see, as you run more and more tests, the number of significant p-values increases. So if you throw in enough stuff in your experiment, you’re pretty much bound to find a p-value less than 0.05. The lesson isn’t that you should just have lots of comparisons in your experiments. The lesson is that the threshold of 5% is no longer appropriate when you have multiple comparisons.
There are ways to correct alpha level (Bonferroni, FDR, etc..) but they shouldn’t be used as a one-size-fits-all solution.
Try it yourself…
- Simulate how power changes across sample sizes for a two-sample t-test.
- Plot your results (sample size on the x axis, power on the y axis).
Increase or decrease your effect size and re-run your simulation/plot. How do sample size and effect size affect power?
experiment <- function(group_size) { # sample data of group size from each of two groups with different means # return p-value of t-test comparing them } power <- function(group_size) { # run experiment 100 times # return the percentage of experiments that have significant p-values } power_levels <- data_frame(group_size = 2:200) %>% mutate(sample_size = group_size * 2, power = map_dbl(group_size, power)) ggplot(power_levels) # add plot structureexperiment <- function(group_size) { sample1 <- rnorm(group_size, 20, 10) sample2 <- rnorm(group_size, 25, 10) p_value <- t.test(sample1, sample2)$p.value return(p_value) } power <- function(group_size) { p_values <- replicate(100, experiment(group_size)) num_sig <- sum(p_values < 0.05) / 100 return(num_sig) } power_levels <- data_frame(group_size = 2:200) %>% mutate(sample_size = group_size * 2, power = map_dbl(group_size, power)) ggplot(power_levels, aes(x = sample_size, y = power)) + geom_hline(yintercept = 0.8, colour = "grey", linetype = "dotted") + geom_point() + geom_smooth()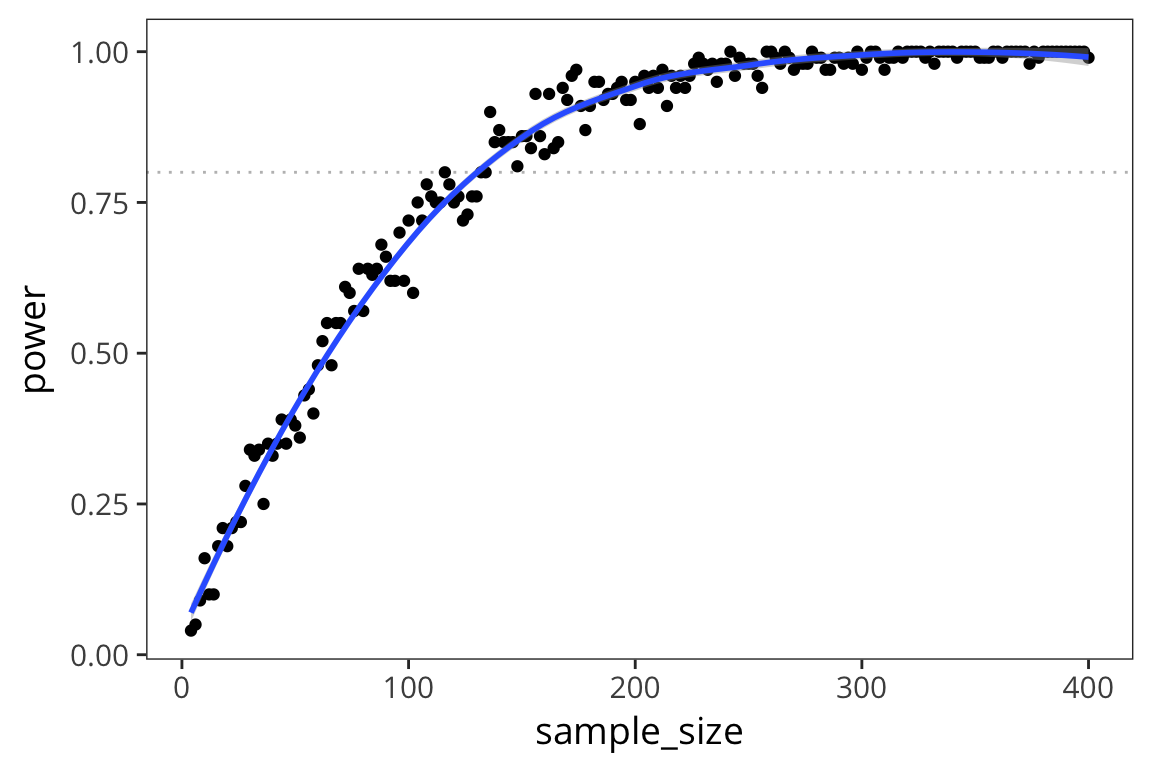
Regression
So far we’ve looked at the types of data where you have samples groups and you want to know if they were generated by the same generative process or two separate ones. But a lot of questions in psycholinguists can’t really be answered in this way. For instance, you can’t use a t-test to look at whether lexical decision times increase as word frequency increases. This is a bivariate relationship between 2 numerical variables.
data_source <- "http://web.mit.edu/psycholinglab/data/"
rts <- read_csv(file.path(data_source, "rts.csv"))
ggplot(rts) +
geom_histogram(aes(x = RTlexdec), bins = 60, color = "white")
ggplot(rts) +
geom_point(aes(x = WrittenFrequency, y = RTlexdec))
So in the past we’ve looked at this using a correlation which tells us about the strength of the relationship between 2 variables. And you can go beyond that and show whether this relationship is statistically significant, i.e., different from 0 or not using cor.test()
cor.test(rts$RTlexdec, rts$WrittenFrequency)##
## Pearson's product-moment correlation
##
## data: rts$RTlexdec and rts$WrittenFrequency
## t = -32.627, df = 4566, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.4580397 -0.4109971
## sample estimates:
## cor
## -0.434815So this looks similar to the output we got from the t-test because what it’s doing is taking the Pearson’s coefficient, r = -0.43, and finding a corresponding t-statistic (specific formula: \(\frac{r\sqrt{n−2}}{\sqrt{1−r^2}}\)), t = -32.63, based on a t-distribution with df = N-2. For this particular t-statistic, the probability that of it occurring given an r = 0 is very very small. So we can conclude that we have a significant correlation.
Note that, in general, a bigger r value is likely to be significant, but you can have a big r value that’s not significant, if you have a very small sample size. You can also have very tiny r values that are significant if you have a big enough sample size.
This is very useful but it’s telling us about how the 2 variables relate to each other without making any hypotheses about the direction of that relationship. Often in experiments we have more specific questions because we have manipulated some variable and we’re looking at how this affects another variable, or we hypothesize that one variable is driving a change in another variable. Correlation says nothing about that. This is where linear regression comes in. For two continuous variables, linear regression and correlation are almost the same but you’ll see that regression is actually much more general because you can use it with categorical predictors, multiple predictors, etc…
We’ve actually been using regression already when we use geom_smooth() to draw a line to fit the data…
ggplot(rts, aes(x = WrittenFrequency, y = RTlexdec)) +
geom_point() +
geom_smooth(method = "lm")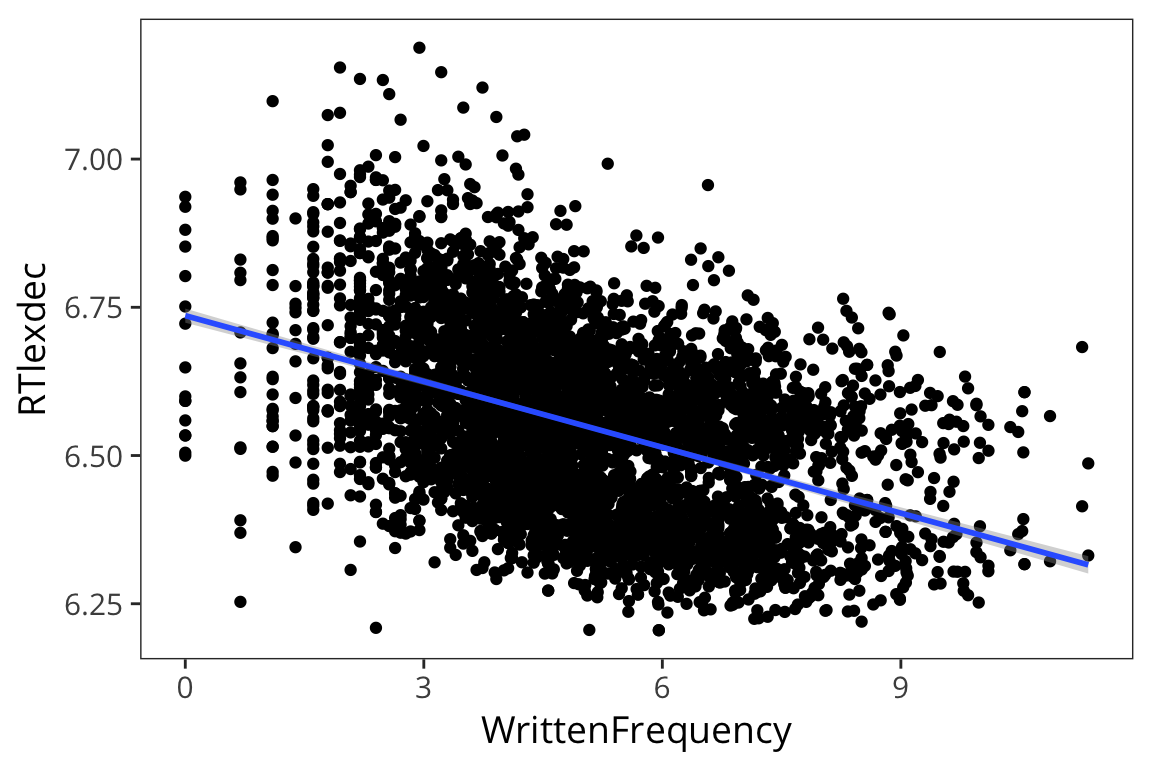
If you remember from high school math class, the formula for a line is \(y = ax + b\). To do linear regression, we’ll use just this:
\[ y_i = \beta_0 + \beta_1 \cdot x_i + \epsilon \]
The \(\beta_0\) is the point at which it intersects with \(x = 0\): the intercept.
The \(\beta_1\) is the change in \(y\) that corresponds to a unit change in \(x\): the slope.
The line that is being drawn by geom_smooth() has an intercept and slope parameter but it also has another key component: error.
freq_lm <- lm(RTlexdec ~ WrittenFrequency, data = rts)
summary(freq_lm)##
## Call:
## lm(formula = RTlexdec ~ WrittenFrequency, data = rts)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.45708 -0.11657 -0.00109 0.10403 0.56085
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.735931 0.006067 1110.19 <2e-16 ***
## WrittenFrequency -0.037010 0.001134 -32.63 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1413 on 4566 degrees of freedom
## Multiple R-squared: 0.1891, Adjusted R-squared: 0.1889
## F-statistic: 1065 on 1 and 4566 DF, p-value: < 2.2e-16There’s a lot of information here so let’s focus first on the coefficients.
library(broom)
tidy(freq_lm, conf.int = TRUE)## # A tibble: 2 x 7
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 6.73593136 0.006067378 1110.18810 0.000000e+00
## 2 WrittenFrequency -0.03701028 0.001134340 -32.62715 4.463918e-210
## # ... with 2 more variables: conf.low <dbl>, conf.high <dbl>First, let’s look at the estimate: the values here are our intercept and slope defining the best fit line.
Those estimates are being compared to a t-distribution in the same way that we’ve done for previous tests and you obtain a p-value. So here this suggests that:
- The intercept value is significantly different from 0, so words with 0 WrittenFrequency have a predicted RTlexdec value of 6.74 seconds.
- The slope is significantly different from 0, so for every unit increase in WrittenFrequency, you expect a unit decrease of 0.04 units of RTlexdec.
So our linear model is:
\[ \text{RTlexdec} = 6.74 - 0.04 \cdot \text{WrittenFrequency} + \mathcal{N}(0, \sigma)\]
In other words for every value of Written Frequency we can find the value of RTlexdec by taking the Written Frequency, multiplying by -0.04 and subtracting that from 6.74, then drawing from a normal distribution centered on that point. Why the normal distribution? That’s the error…
freq_aug <- augment(freq_lm)
head(freq_aug)## # A tibble: 6 x 9
## RTlexdec WrittenFrequency .fitted .se.fit .resid .hat
## * <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 6.543754 3.912023 6.591146 0.002440312 -0.04739273 0.0002981668
## 2 6.397596 4.521789 6.568579 0.002166358 -0.17098259 0.0002349790
## 3 6.304942 6.505784 6.495150 0.002684846 -0.19020818 0.0003609169
## 4 6.424221 5.017280 6.550240 0.002090998 -0.12601990 0.0002189151
## 5 6.450597 4.890349 6.554938 0.002096251 -0.10434136 0.0002200163
## 6 6.531970 4.770685 6.559367 0.002110206 -0.02739665 0.0002229556
## # ... with 3 more variables: .sigma <dbl>, .cooksd <dbl>, .std.resid <dbl>ggplot(freq_aug, aes(x = WrittenFrequency, y = RTlexdec)) +
geom_point() +
geom_point(aes(y = .fitted), color = "blue")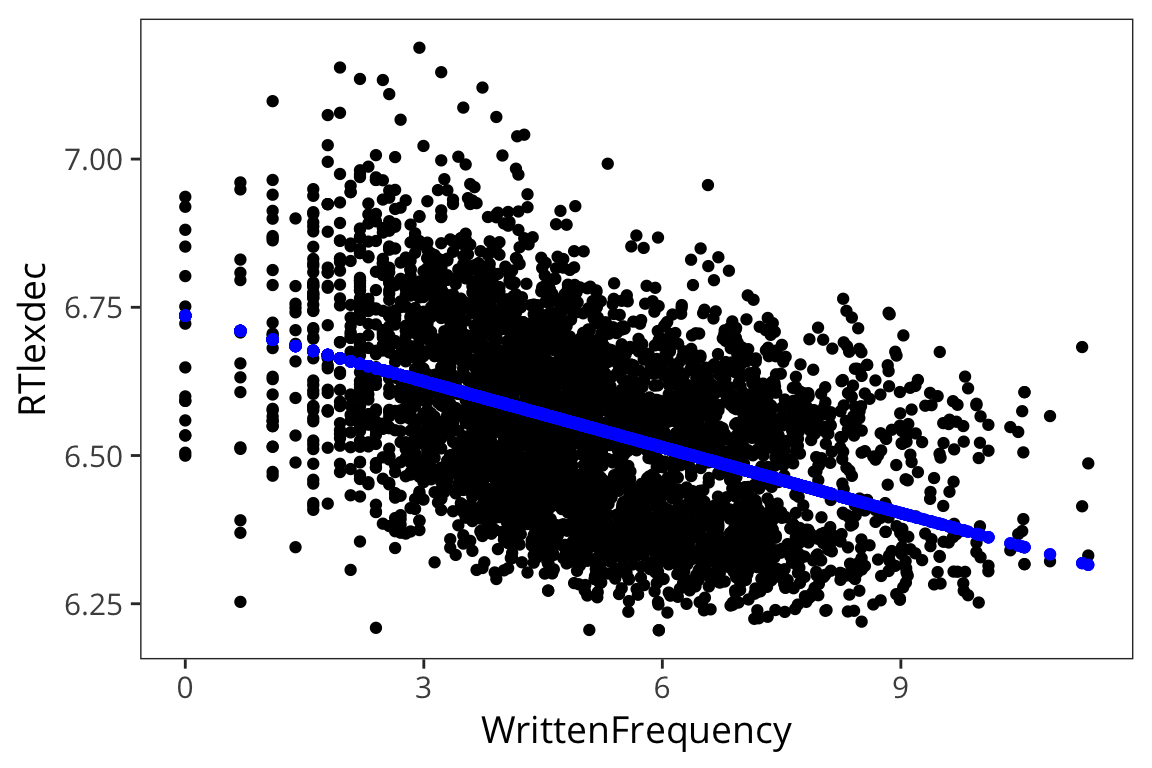
So clearly the real values don’t fall exactly on the line like the predicted values. The line is not a perfect fit and it couldn’t be – there is no line that would fit every single one of those datapoints. The distances between the real datapoints and this line is what’s called error.
errors <- freq_aug$RTlexdec - freq_aug$.fitted
residuals <- freq_aug$.resid
all.equal(errors, residuals)## [1] TRUEggplot(freq_aug, aes(sample = .resid)) +
stat_qq()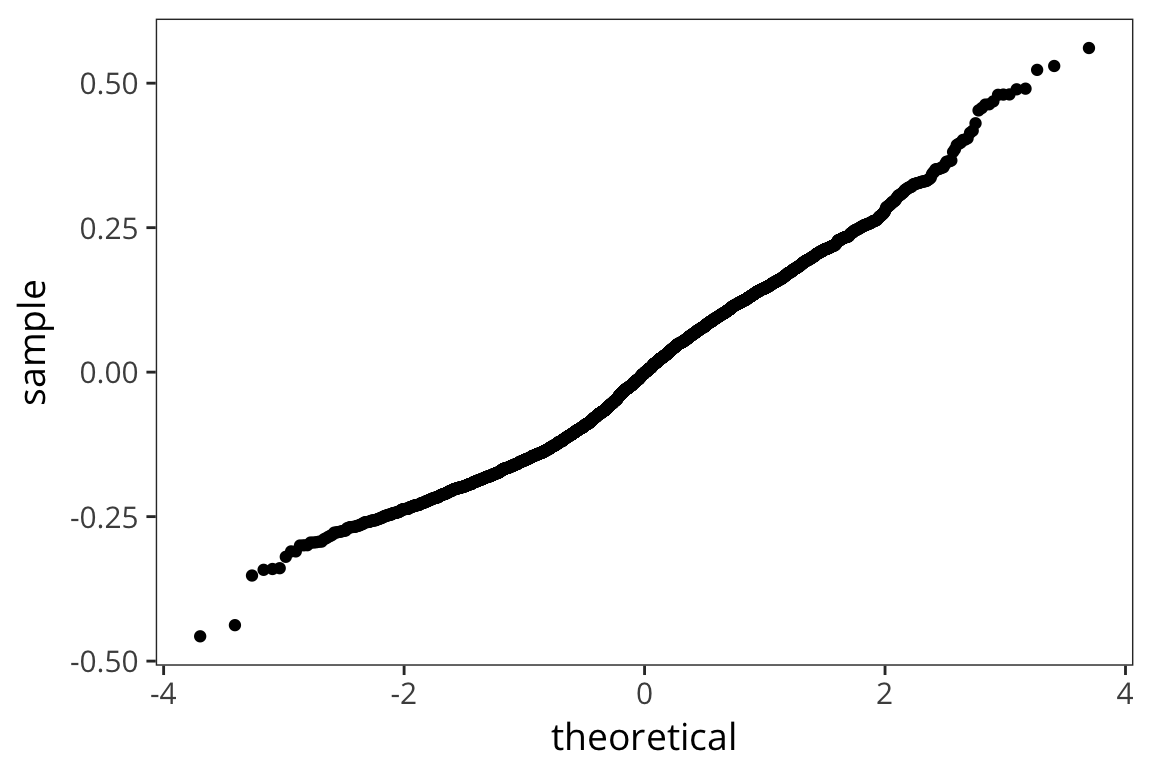
ggplot(freq_aug, aes(x = WrittenFrequency, y = .resid)) +
geom_point() +
geom_hline(yintercept = 0, color = "blue")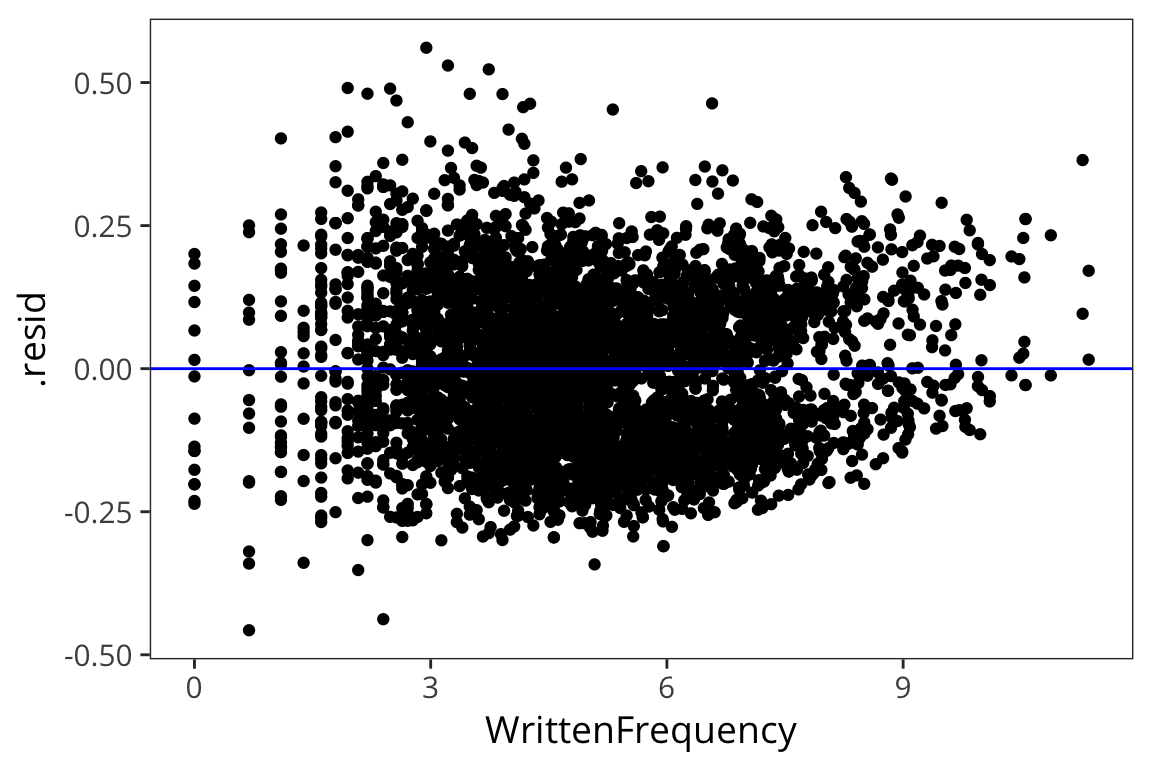
The residuals are normally distributed which is good – this is the mark of an appropriately applied linear regression model. We’re also not seeing any huge differences in the residuals for different values of x (homoscedasticity).
The residuals are the part of the data that we have failed to explain with our model. So we want them to be minimized. In fact, minimizing those residuals is pretty much how the best fit line is picked. (I don’t think we need to get into all the detail about this but sum of the squared distances between each point and the line is what is being minimized: http://students.brown.edu/seeing-theory/regression/index.html#first)
http://shinyapps.org/showapp.php?app=http://87.106.45.173:3838/felix/lmfit&by=Felix%20Sch%C3%B6nbrodt&title=Find-a-fit!&shorttitle=Find-a-fit
The deviation in residuals appears in the summary as “residual standard error”.
sd(freq_aug$.resid)## [1] 0.1413085summary(freq_lm)##
## Call:
## lm(formula = RTlexdec ~ WrittenFrequency, data = rts)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.45708 -0.11657 -0.00109 0.10403 0.56085
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.735931 0.006067 1110.19 <2e-16 ***
## WrittenFrequency -0.037010 0.001134 -32.63 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1413 on 4566 degrees of freedom
## Multiple R-squared: 0.1891, Adjusted R-squared: 0.1889
## F-statistic: 1065 on 1 and 4566 DF, p-value: < 2.2e-16So once you’ve found this optimal line and you have those predicted/fitted values, you can assess whether this line is actually explaining a lot of the variation in the data or not. This is the same as asking whether variation in \(x\) explains variation in \(y\) well or not. You can do this by seeing how close the fitted values are to the actual \(y\) values.
(cor(freq_aug$.fitted, freq_aug$RTlexdec)) ^ 2## [1] 0.1890641It is often interpreted as the proportion of data which your model explains. So frequency here explains 18.9% of the observed variation in RTs. The F-test at the very bottom is saying that \(r^2\) is significantly different from 0, i.e. the model is explaining a non-zero portion of the variance.
freq_lm_null <- lm(RTlexdec ~ 1, data = rts)
rss_null <- sum(residuals(freq_lm_null) ^ 2)
rss <- sum(residuals(freq_lm) ^ 2)
n <- nrow(rts)
p_null <- 1
p <- 2
f_value <- ((rss_null - rss) / (p - p_null)) / (rss / (n - p - 1))
pf(f_value, p - p_null, n - p, lower.tail = FALSE)## [1] 4.906935e-210This is not a particularly useful value for our purposes, it’ll usually be significant…
Try it yourself…
- Model the relationship between RTlexdec and WrittenSpokenFrequencyRatio, plot it, and summarize in words what the result means.
Now look at the relationship between RTnaming and WrittenSpokenFrequencyRatio. Do you notice anything different?
ratio_lm <- lm(RTlexdec ~ WrittenSpokenFrequencyRatio, data = rts) ratio_tidy <- tidy(ratio_lm) ratio_aug <- augment(ratio_lm) summary(ratio_lm)## ## Call: ## lm(formula = RTlexdec ~ WrittenSpokenFrequencyRatio, data = rts) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.34617 -0.12579 0.00009 0.10287 0.63242 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 6.546463 0.002684 2438.935 < 2e-16 *** ## WrittenSpokenFrequencyRatio 0.005364 0.001992 2.693 0.00711 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.1568 on 4566 degrees of freedom ## Multiple R-squared: 0.001586, Adjusted R-squared: 0.001367 ## F-statistic: 7.251 on 1 and 4566 DF, p-value: 0.00711ggplot(ratio_aug, aes(sample = .resid)) + stat_qq()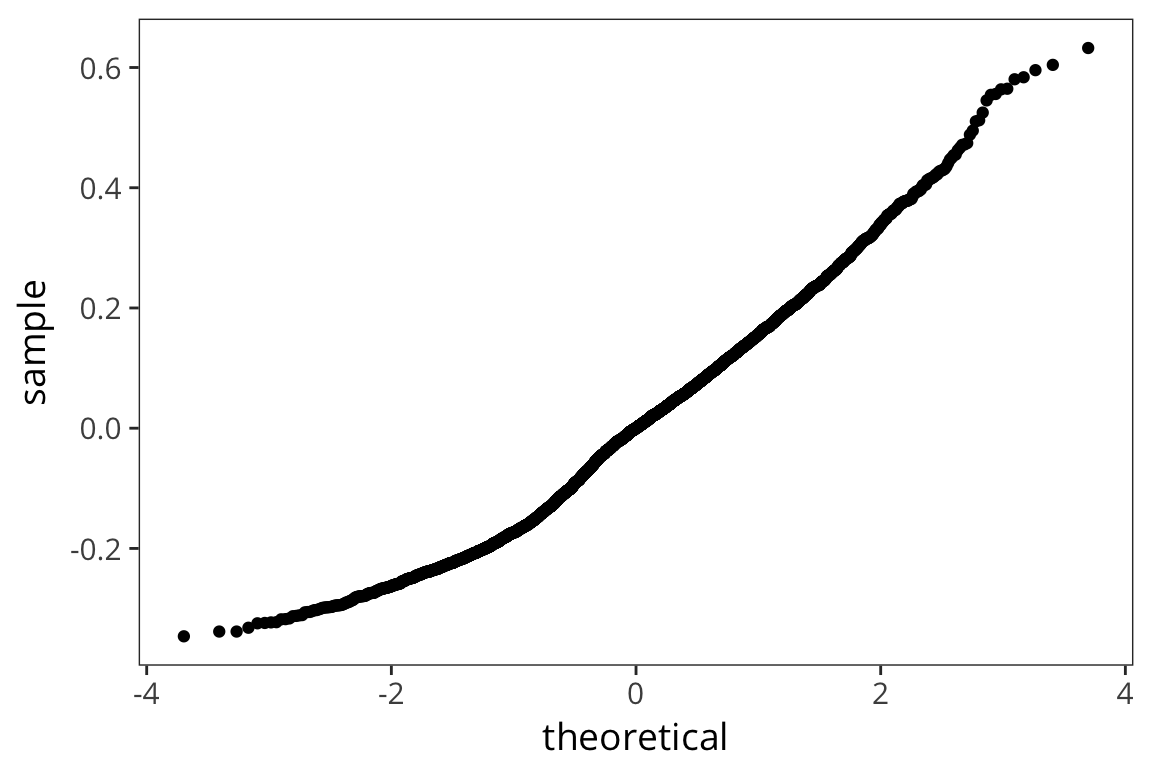
ggplot(ratio_aug, aes(x = WrittenSpokenFrequencyRatio, y = RTlexdec)) + geom_point(color = "grey") + geom_abline(intercept = filter(ratio_tidy, term == "(Intercept)")$estimate, slope = filter(ratio_tidy, term == "WrittenSpokenFrequencyRatio")$estimate, colour = "blue") + geom_smooth(method = lm, colour = "red")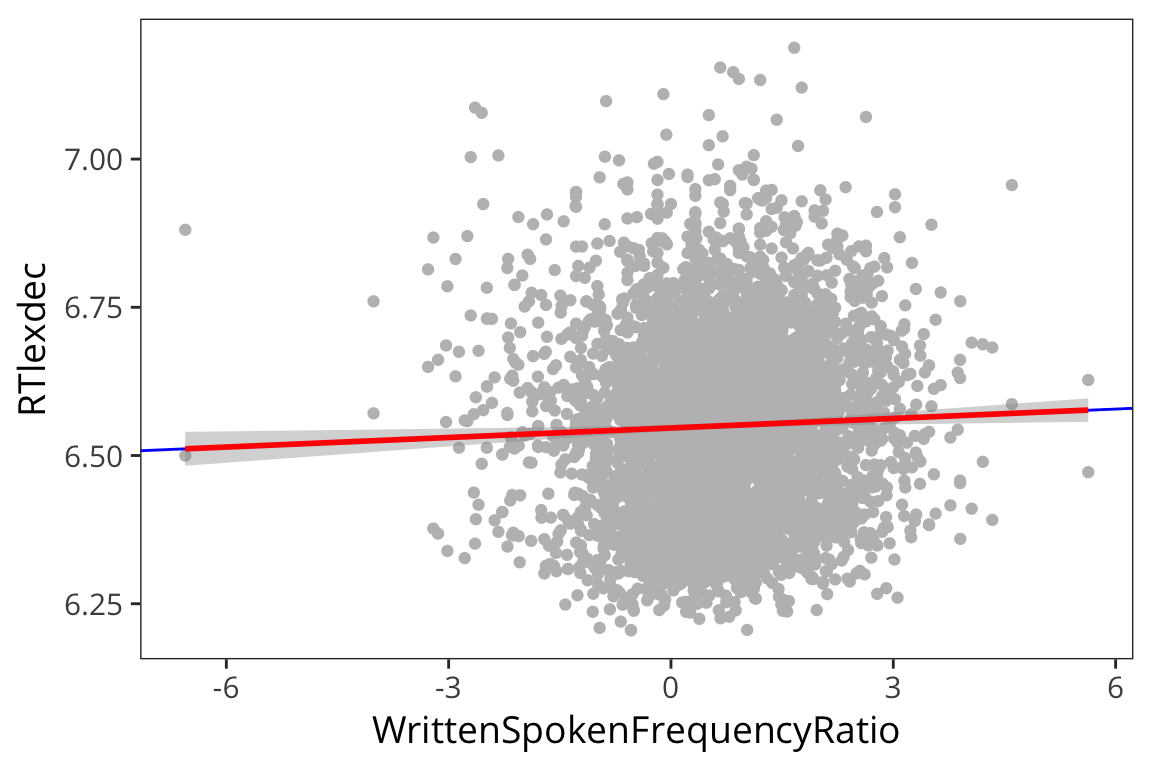
naming_lm <- lm(RTnaming ~ WrittenSpokenFrequencyRatio, data = rts) naming_aug <- augment(naming_lm) summary(naming_lm)## ## Call: ## lm(formula = RTnaming ~ WrittenSpokenFrequencyRatio, data = rts) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.29190 -0.17437 0.01484 0.16785 0.37799 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 6.318707 0.003053 2069.426 <2e-16 *** ## WrittenSpokenFrequencyRatio 0.005606 0.002266 2.474 0.0134 * ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.1784 on 4566 degrees of freedom ## Multiple R-squared: 0.001339, Adjusted R-squared: 0.00112 ## F-statistic: 6.122 on 1 and 4566 DF, p-value: 0.01339ggplot(naming_aug, aes(sample = .resid)) + stat_qq()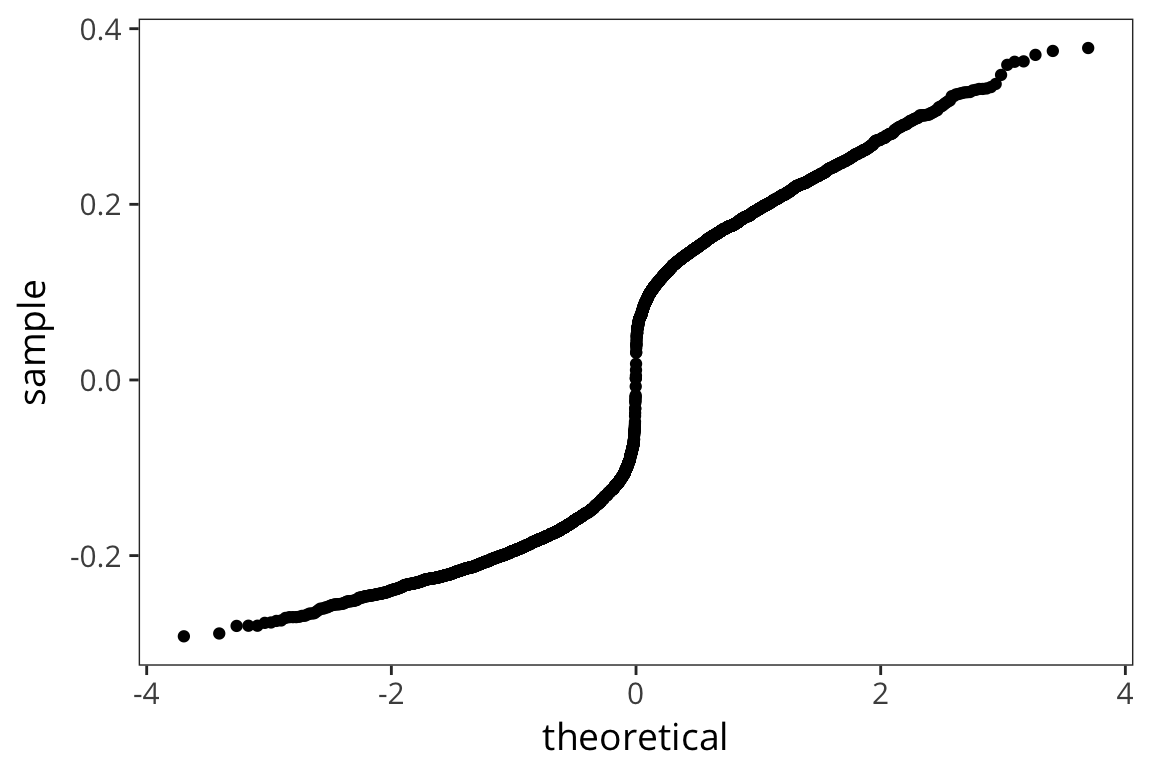
ggplot(naming_aug, aes(x = WrittenSpokenFrequencyRatio, y = RTnaming)) + geom_point(color = "grey") + geom_smooth(method = lm, colour = "red")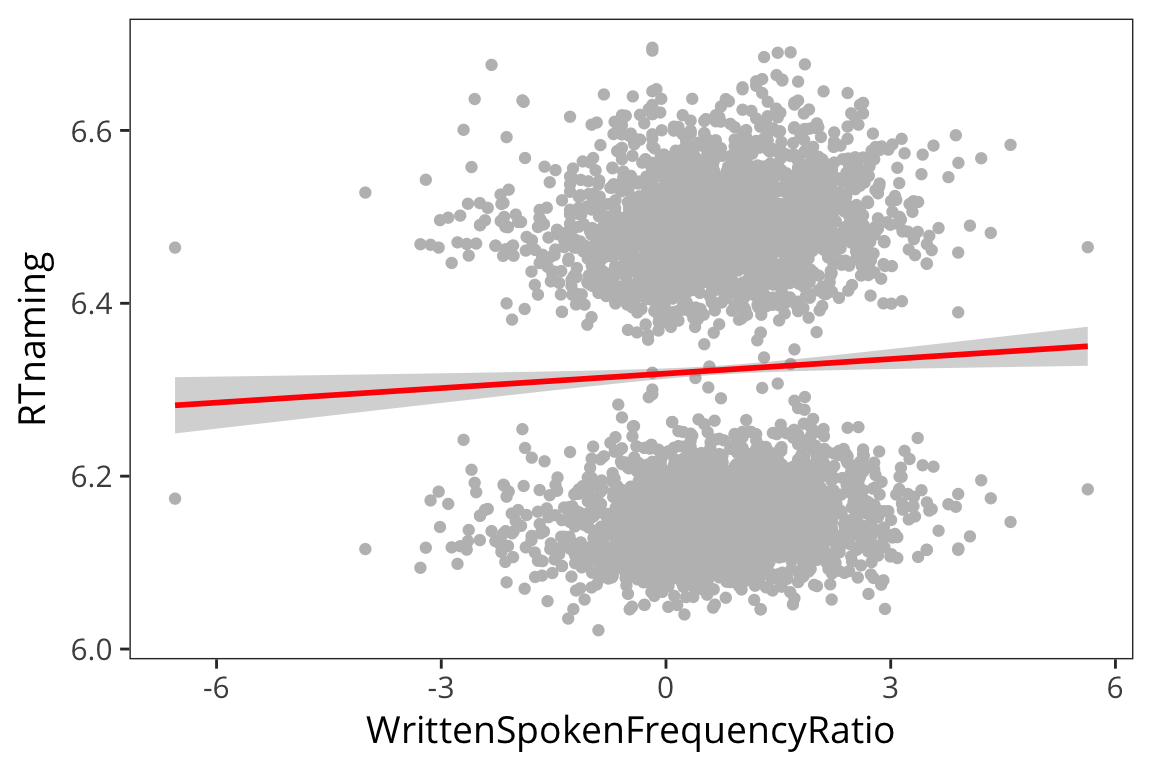
Here we looked at one continuous predictor and a continuous outcome, but regression is much more general than that. So we’re going to look at a few other ways you can use it.
Categorical predictors
Let’s say we want to look at the effect of being in one of 2 (or more) groups on some response. For example, we can look at RTlexdec as a function of the age of the subjects
rts_age <- rts %>%
group_by(AgeSubject) %>%
summarise(mean_rt = mean(RTlexdec))
ggplot(rts, aes(x = AgeSubject, y = RTlexdec)) +
geom_violin() +
geom_point(aes(y = mean_rt), data = rts_age, size = 3)
age_lm <- lm(RTlexdec ~ AgeSubject, data = rts)
summary(age_lm)##
## Call:
## lm(formula = RTlexdec ~ AgeSubject, data = rts)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.25776 -0.08339 -0.01669 0.06921 0.52685
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.660958 0.002324 2866.44 <2e-16 ***
## AgeSubjectyoung -0.221721 0.003286 -67.47 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1111 on 4566 degrees of freedom
## Multiple R-squared: 0.4992, Adjusted R-squared: 0.4991
## F-statistic: 4552 on 1 and 4566 DF, p-value: < 2.2e-16This looks very familiar but if we go back to our line equation, something is weird.
\[ \text{RTlexdec} = 6.66 - 0.22 \cdot \text{AgeSubject} + \mathcal{N}(0, \sigma)\]
How do you multiply AgeSubject, which is either the word “old” or the word “young”, by a number?
Turns out R automatically turns “old” and “young” into 0s and 1s.
But you can’t see this until you convert it into a factor…
rts$AgeSubject <- factor(rts$AgeSubject)
contrasts(rts$AgeSubject)## young
## old 0
## young 1It is treating “old” as 0 and “young” as 1 and it just did this alphabetically by default. This is called dummy coding.
So how do we read the output of our model?
age_tidy <- tidy(age_lm)
age_tidy## # A tibble: 2 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 6.6609581 0.002323772 2866.4417 0
## 2 AgeSubjectyoung -0.2217215 0.003286310 -67.4682 0The Intercept corresponds to the y value when the dummy coded variable is 0, so the intercept is the average RTlexdec for old people.
rts_age## # A tibble: 2 x 2
## AgeSubject mean_rt
## <chr> <dbl>
## 1 old 6.660958
## 2 young 6.439237AgeSubjectyoung is the coefficient that you add when the dummy coded variable is 1. So the average RTlexdec for young people is -0.22 less than the intercept.
intercept <- filter(age_tidy, term == "(Intercept)")$estimate
slope <- filter(age_tidy, term == "AgeSubjectyoung")$estimate
old_code <- contrasts(rts$AgeSubject)["old", ]
young_code <- contrasts(rts$AgeSubject)["young", ]
# old RTs
intercept + slope * old_code## [1] 6.660958# young RTs
intercept + slope * young_code## [1] 6.439237Dummy coding vs. effects coding
Another option is to do what is sometimes called effects coding. Instead of the default dummy coding that R assigns, you can change the contrast codes to something that is more meaningful to you.
contrasts(rts$AgeSubject) <- c(-0.5, 0.5)
contrasts(rts$AgeSubject)## [,1]
## old -0.5
## young 0.5So now the indicator variable for AgeSubject is -0.5 for “old” and 0.5 for “young”.
How will this affect our regression?
age_lm_2 <- lm(RTlexdec ~ AgeSubject, data = rts)
age_tidy_2 <- tidy(age_lm_2)
summary(age_lm_2)##
## Call:
## lm(formula = RTlexdec ~ AgeSubject, data = rts)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.25776 -0.08339 -0.01669 0.06921 0.52685
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.550097 0.001643 3986.29 <2e-16 ***
## AgeSubject1 -0.221721 0.003286 -67.47 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1111 on 4566 degrees of freedom
## Multiple R-squared: 0.4992, Adjusted R-squared: 0.4991
## F-statistic: 4552 on 1 and 4566 DF, p-value: < 2.2e-16As you can see the slope is exactly the same – it’s still telling us that going from old to young (1 unit change) means subtracting -0.22. But note that the intercept is different. Now the intercept is the grand mean (across all conditions).
What if we rewrite our formulas from earlier:
intercept <- filter(age_tidy_2, term == "(Intercept)")$estimate
slope <- filter(age_tidy_2, term == "AgeSubject1")$estimate
old_code <- contrasts(rts$AgeSubject)["old", ]
young_code <- contrasts(rts$AgeSubject)["young", ]
# old RTs
intercept + slope * old_code## old
## 6.660958# young RTs
intercept + slope * young_code## young
## 6.439237We still get the exact same thing. In this case, where there’s just one predictor, the choice of contrast coding is entirely a matter of preference. In multiple regression, where you have many predictors potentially interacting, the right contrast coding can make a huge difference for how you interpret what’s going on in your model, specifically whether you are looking at simple effects or main effects.
There are many different coding schemes for testing various hypotheses, more examples: https://stats.idre.ucla.edu/r/library/r-%20library-contrast-coding-systems-for-%20categorical-variables/
Multiple Predictors
Now remember when we looked at the histogram, we saw that the RTs aren’t quite normally distributed in that there were two peaks. And now we know that young and old subjects respond differently. Let’s incorporate that into our regression. First some plots:
ggplot(rts, aes(x = WrittenFrequency, y = RTlexdec, colour = AgeSubject)) +
geom_point(alpha = 0.1)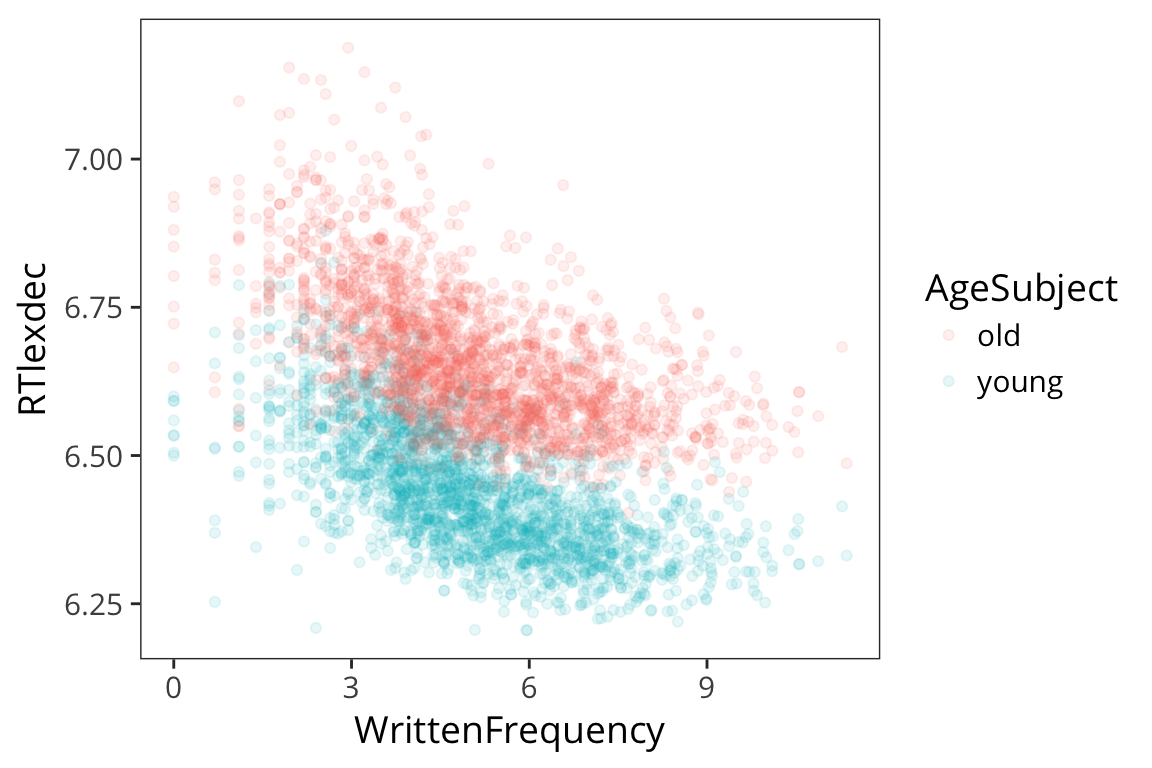
We see there are two groups here. Remember we are evaluating our model by seeing how close the fitted values are to the real data points, and we can get a lot closer if we have different lines for different age.
ggplot(rts, aes(x = WrittenFrequency, y = RTlexdec, colour = AgeSubject)) +
geom_point(alpha = 0.1) +
geom_smooth(method = "lm")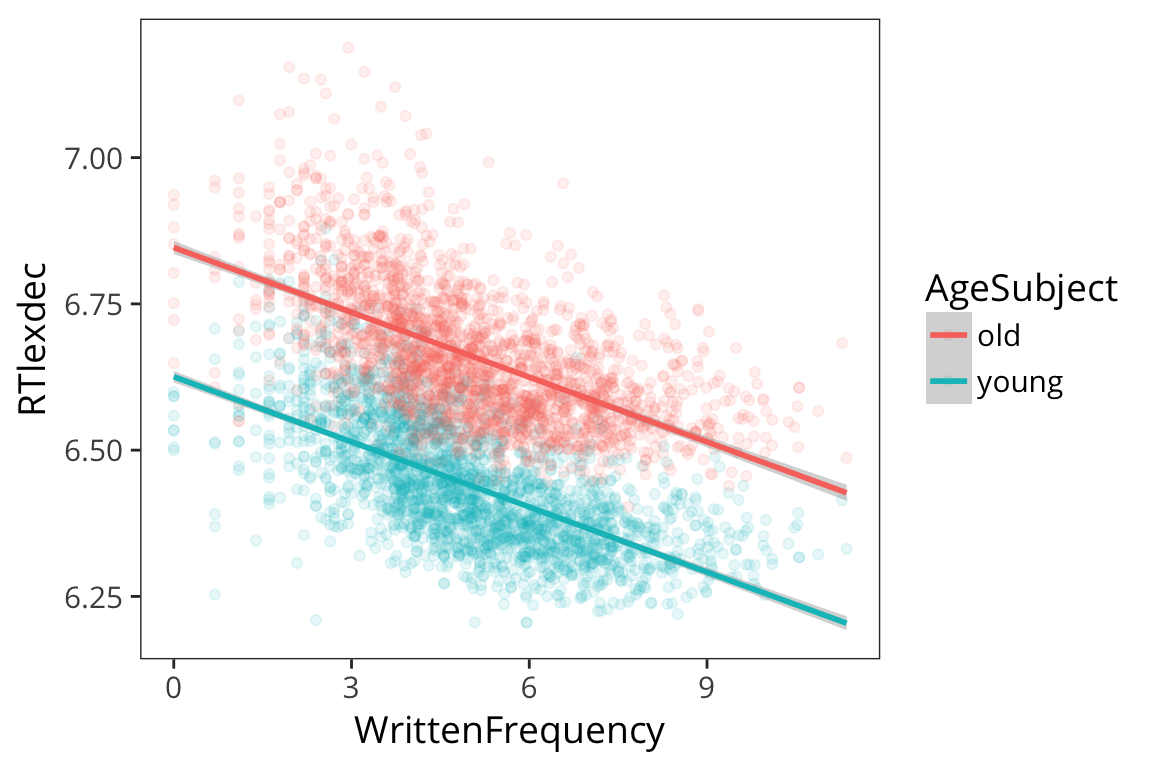
Let’s make a regression model with multiple predictors:
\[ \text{RTlexdec} = \beta_0 + \beta_1 \cdot \text{WrittenFrequency} + \beta_2 \cdot \text{AgeSubject} + \mathcal{N}(0, \sigma)\]
freq_age_lm <- lm(RTlexdec ~ WrittenFrequency + AgeSubject, data = rts)
summary(freq_age_lm)##
## Call:
## lm(formula = RTlexdec ~ WrittenFrequency + AgeSubject, data = rts)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.34622 -0.06029 -0.00722 0.05178 0.44999
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.7359314 0.0037621 1790.48 <2e-16 ***
## WrittenFrequency -0.0370103 0.0007033 -52.62 <2e-16 ***
## AgeSubject1 -0.2217215 0.0025930 -85.51 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.08763 on 4565 degrees of freedom
## Multiple R-squared: 0.6883, Adjusted R-squared: 0.6882
## F-statistic: 5040 on 2 and 4565 DF, p-value: < 2.2e-16So now we have the intercept, which is the mean of RTlexdec for WrittenFrequency = 0 and across all AgeSubject (because of the effects coding).
The effect of WrittenFrequency (-0.037) is pretty much the same as before which makes sense because we were seeing the same effect of Written Frequency in both groups
The effect of age is very similar in size to when it was the sole predictor in the model as well.
Note that both the effects of Age and Frequency are significant suggesting that they are both independently contributing to explaining the variance in RTlexdec.
Critically, the \(r^2\) is much larger, suggesting we’re doing a much better job of fitting the data than with the previous model. All that extra variance is now being explained by adding the Age factor.
Linear model: \[ y_i = \beta_0 + \beta_1 \cdot x_{i1} + \beta_2 \cdot x_{i2} + \ldots + \beta_k \cdot x_{ik} + \epsilon_i \]