2.972 How A Gear Pump Works

TITLE:          How A Gear Pump Works
AUTHOR:    Martin L. Culpepper
COURSE:     2
YEAR:          G

MAIN FUNCTIONAL REQUIREMENT: Convert mechanical power into fluid power.

DESIGN PARAMETER: Pump (a gear pump is one type of pump which can satisfy this functional requirement)

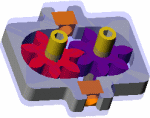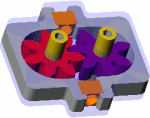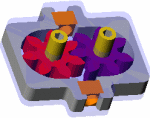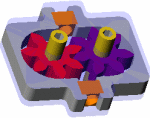
GEOMETRY/STRUCTURE AND PARTS:

real_pump_front_view.jpg (8010 bytes)

real_gear_pump_exploded.jpg (30840 bytes)

EXPLANATION OF HOW IT WORKS:

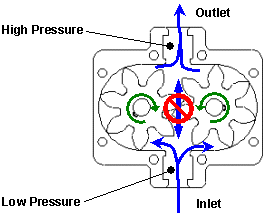
flow_thru_gear_pump.gif (7137 bytes)

One shaft is driven by a motor or some other means

The gear mounted to this shaft (driving gear) engages the other gear (driven gear)

Fluid on the inlet side flows into and is trapped between the rotating gear teeth and the housing

The fluid is carried around the outside of the gears to the outlet side of the pump

As the fluid can not seep back along the path it came, nor between the engaged gear teeth (they create a seal,) it must exit the outlet port.

In some gear pumps, there are side plates usually made of brass which can be replaced or re-ground when the gap between the face of the gear and the end housing becomes too large

DOMINANT PHYSICS:

Variable	Description	Metric Units	English Units
P_in	Power input to shaft	Watts	Horsepower
P_out	Power output to fluid system	Watts	Horsepower
P_loss	Power loss (i.e. to coloumb friction and viscous dissipation)	Watts	Horsepower
w	Shaft rotational speed	rad/s	RPM
Dp	Pressure increase between inlet and outlet	Pascals	psi
Q	Flow rate through the pump	liters³/s	in³/s
h_m	Mechanical efficiency	---	---

The pump takes power from a rotating shaft:

P_in = T x w

A portion of this power is dissipated in the pump through coloumb friction and viscous dissipation. This is not easily quantified theoretically and is often determined experimentally. This power will be denoted at P_loss.

P_loss = f(friction, viscous effects......)

Some fluid will seep through the gap between the sides of the gears and the endplates (see figure below.) This gap must be small in order to maintain the pressure increase across the pump. Increasing the gap diminishes the pumps ability to hold a pressure difference between the inlet and outlet. The gap is typically around 0.0005 inches.

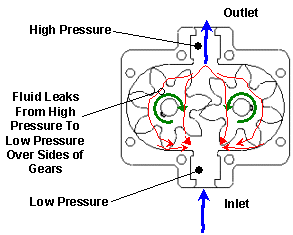
gear_pump_gear_face_leakage.gif (8072 bytes)

The power which can then be derived from the fluid which comes out of the pump is:

P_out = (Dp x Q) = P_in - P_loss = T x w - P_loss

This can also be expressed using the efficiency:

P_out = h_m x P_in

LIMITING PHYSICS

The performance/use of the pump is limited by its:

Efficiency

h_m=of a pump is P_out/P_in. This is a function of the fluid viscosity, clearance between internal components, friction between mating components, and other variables.

Typically, gear pumps have efficiencies around 85%.

Bearings

Many external gear pumps use journal bearings to support the rotating shafts. In order for these bearings to work, a minimum speed is required (depends upon pressure of the pump.) In addition to imposing limits on the operational speed, in many cases, the bearings determine the maximum pressure the pump can operate at. Should the pressure drop across the pump be too large, the journal bearings will not be able to support the loads on the shafts (which come mainly from the pressure difference.)

IF NEEDED, PLOTS/GRAPHS/TABLES:

None to include here

WHERE YOU CAN FIND GEAR PUMPS:

These pumps have few moving parts, making them inexpensive. These pumps are typically used where low to medium pressure (about 2500 - 4000 psi) is needed and mechanical efficiency is not extremely important (typical efficiency is about 85%.)

You can find gear pumps on the following machines:

Usually your car's oil pump
Hydraulically driven lawn care equipment
Some hydraulically driven log splitters
Hydraulic power units on trucks and construction equipment
Metering applications (gear pumps are good at controlling volume flow rate)

REFERENCES/MORE INFORMATION:

Viking Pump's Web Page on External Gear Pumps

Don't forget to add book had on hydraulic component design

Others....