Manned Operations
	Introducing EVE Hull Design Exostructure Power Propulsion Docking Ballast Sensors & Sampling Manipulators Life Support Navigation Communication Viewing Systems Control Systems ROV

Hull Design

Hull design is one of the most important aspects of the design of a submersible. There are many decisions to make, including:

1. Shape.
2. Dimensions.
3. Construction materials.

We shall deal with each in turn. As a start, let us consider the shape. What are the main characteristics of a good shape for the hull?

1. It maximizes the volume in which the scientists can work. Of course, 'maximizes' here is the wrong word, because the size of our submarine can go to infinity, but there are constraints which stop us from building a submarine the size of a football field as you will shortly see.
2. Minimizes costs. After all, Atlantis II is on a limited budget. This translates to the hull having minimum surface area, since most of the expensive titanium alloy, the material we will use to construct the hull, will go into building the submersibles walls.
3. Maximizes the strength of the submarine so that it does not collapse under the huge water pressure. Of course, we could be lousy engineers and build walls one meter thick, making our submersible incredibly strong. But then, other aspects of the mission would be left with no funding at all and the scientists in the submersibles would be cramped into a very small volume. So we have to choose our shape carefully so that it inherently provides the required strength and eliminates the need for very thick walls.
4. Minimizes drag and thus maximizes speed. More speed means less time, less consumption of resources like fuel and oxygen, and more work done.
As you can see, shape matters.

A sphere is the 3-dimensional shape with the minimum surface area that encloses a fixed volume. A sphere is also a very strong structure (although there are even stronger structures, like a sphere whose surface is made of triangles.) So should we go ahead and use a sphere? Well, many submersibles have done so. But that does not mean that spheres are perfect. They have one problem, drag. They experience very high levels of drag. So, how do we calculate the drag on an object? We use the following equation:

The coefficient of drag is a function of Reynolds number, Re, which in turn can be calculated using this equation:

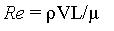
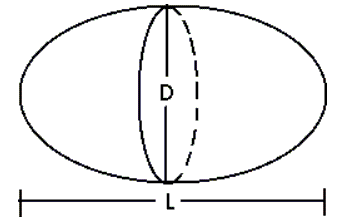
L is a characteristic length of the body, while µ is the fluid’s viscosity. For spheres, cylinders and discs, L is simply the diameter. The density and the viscosity will be constants in our case, and they are those the sea water through which the submersible will move. Let us consider how changing the shape will affect the drag if we are to move at a constant velocity (V). Now, Re and thus the drag coefficient depends solely on the shape. Let's look at the following table illustrating how the drag coefficient varies with shape:

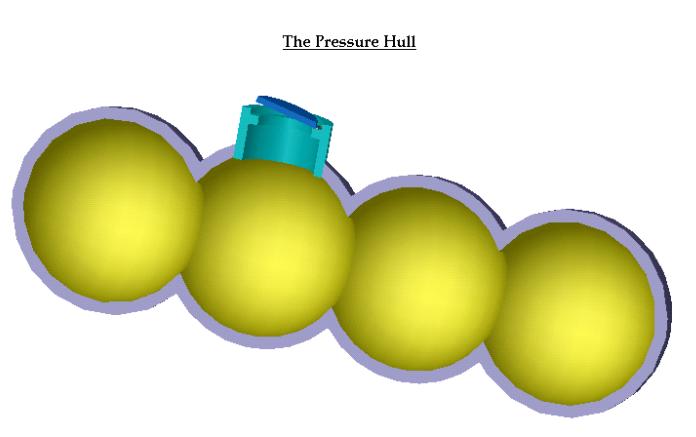
The first row in the table describes a sphere. As the hull becomes more elongated, its shape becomes almost a cylinder with hemispherical ends and its drag coefficient decreases. But at the same time, as the length of the hull increases frictional drag (another type of drag) increases. Also, the strength due to spherical structure is lost. So elongation is good, but only to a certain extent. To solve this problem, we have decided to use a hybrid structure for our cylinder, multiple intersecting spheres. This structure has the required strength due to the spheres and the hydrodynamic advantages of a cylinder. The structure is show below.

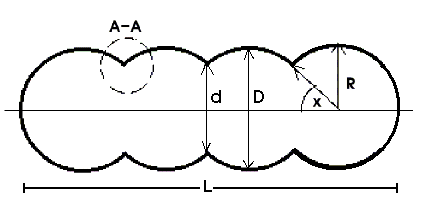
The spheres are reinforced at their intersections by rings that can be made of the same material out of which the hull is made or a lighter material to increase buoyancy. The buoyancy factor for intersecting spheres is a function of R (radius of a single sphere), x (angle of shell intersection), the thickness of the shell, the number of intersection rings, as well as other factors.

Another advantage of this structure is the good internal arrangement we would obtain if we use it. It is pretty hard to make use of the space in a big sphere. How would the upper half of the sphere be made use of if the scientists will occupy mainly the lower half? On the other hand, this arrangement constituting of smaller spheres allows the more natural 'horizontal spreading' of equipment and gives the scientists more space to work in.

Next, we consider dimensions. We have studied how much internal space we need and decided on the following dimensions.

Outer diameter: 2.2m.
Inner diameter (D): 2m.
Thickness of hull’s wall’s: 10cm.
Length: 7.2m.
Number of spheres: 4.
Angle of intersection (x): 30°.

The material out of which the hull will be made is a titanium graphite alloy. Although such an alloy is expensive, it is light, strong and corrosion resistant, three factors which are important in the material out of which a pressure hull is made.

The pressure hull is designed to go to depths of 5000m before collapsing. The depth we will be working at is 3000m, which means that the pressure hull is very safe.

Below is a 3D picture of EVE's pressure hull: