HMWSoln Class Reference
[Thermodynamic Properties]
Class HMWSoln represents a dilute or concentrated liquid electrolyte phase which obeys the Pitzer formulation for nonideality. More...
#include <HMWSoln.h>
Public Member Functions | |
| HMWSoln () | |
| Default Constructor. | |
| HMWSoln (std::string inputFile, std::string id="") | |
| Construct and initialize an HMWSoln ThermoPhase object directly from an asci input file. | |
| HMWSoln (XML_Node &phaseRef, std::string id="") | |
| Construct and initialize an HMWSoln ThermoPhase object directly from an XML database. | |
| HMWSoln (const HMWSoln &right) | |
| Copy Constructor. | |
| HMWSoln & | operator= (const HMWSoln &right) |
| Asignment operator. | |
| HMWSoln (int testProb) | |
| This is a special constructor, used to replicate test problems during the initial verification of the object. | |
| virtual | ~HMWSoln () |
| Destructor. | |
| ThermoPhase * | duplMyselfAsThermoPhase () const |
| Duplicator from the ThermoPhase parent class. | |
| virtual void | setParameters (int n, doublereal *const c) |
| Set the equation of state parameters. | |
| virtual void | getParameters (int &n, doublereal *const c) const |
| Get the equation of state parameters in a vector. | |
| virtual void | setParametersFromXML (const XML_Node &eosdata) |
| Set equation of state parameter values from XML entries. | |
| SpeciesThermo & | speciesThermo () |
| Return a reference to the species thermodynamic property manager. | |
| void | constructPhaseFile (std::string inputFile, std::string id) |
| Initialization of a HMWSoln phase using an xml file. | |
| void | constructPhaseXML (XML_Node &phaseNode, std::string id) |
| Import and initialize a HMWSoln phase specification in an XML tree into the current object. | |
| virtual void | initThermo () |
| Internal initialization required after all species have been added. | |
| virtual void | initThermoXML (XML_Node &phaseNode, std::string id) |
| Initialize the phase parameters from an XML file. | |
| double | speciesMolarVolume (int k) const |
| Report the molar volume of species k. | |
| virtual double | A_Debye_TP (double temperature=-1.0, double pressure=-1.0) const |
| Value of the Debye Huckel constant as a function of temperature and pressure. | |
| virtual double | dA_DebyedT_TP (double temperature=-1.0, double pressure=-1.0) const |
| Value of the derivative of the Debye Huckel constant with respect to temperature as a function of temperature and pressure. | |
| virtual double | dA_DebyedP_TP (double temperature=-1.0, double pressure=-1.0) const |
| Value of the derivative of the Debye Huckel constant with respect to pressure, as a function of temperature and pressure. | |
| double | ADebye_L (double temperature=-1.0, double pressure=-1.0) const |
| Return Pitzer's definition of A_L. | |
| double | ADebye_J (double temperature=-1.0, double pressure=-1.0) const |
| Return Pitzer's definition of A_J. | |
| double | ADebye_V (double temperature=-1.0, double pressure=-1.0) const |
| Return Pitzer's definition of A_V. | |
| virtual double | d2A_DebyedT2_TP (double temperature=-1.0, double pressure=-1.0) const |
| Value of the 2nd derivative of the Debye Huckel constant with respect to temperature as a function of temperature and pressure. | |
| double | AionicRadius (int k=0) const |
| Reports the ionic radius of the kth species. | |
| int | formPitzer () const |
| formPitzer(): | |
| void | printCoeffs () const |
| Print out all of the input coefficients. | |
| void | getUnscaledMolalityActivityCoefficients (doublereal *acMolality) const |
| Get the array of unscaled non-dimensional molality based activity coefficients at the current solution temperature, pressure, and solution concentration. | |
| int | debugPrinting () |
| Return int specifying the amount of debug printing. | |
| virtual void | setStateFromXML (const XML_Node &state) |
| Set equation of state parameter values from XML entries. | |
| void | setState_TPM (doublereal t, doublereal p, const doublereal *const molalities) |
| Set the temperature (K), pressure (Pa), and molalities (gmol kg-1) of the solutes. | |
| void | setState_TPM (doublereal t, doublereal p, compositionMap &m) |
| Set the temperature (K), pressure (Pa), and molalities. | |
| void | setState_TPM (doublereal t, doublereal p, const std::string &m) |
| Set the temperature (K), pressure (Pa), and molalities. | |
| virtual std::string | report (bool show_thermo=true) const |
| returns a summary of the state of the phase as a string | |
| doublereal | _RT () const |
| Return the Gas Constant multiplied by the current temperature. | |
| bool | chargeNeutralityNecessary () const |
| Returns the chargeNeutralityNecessity boolean. | |
| XML_Node & | xml () |
| Returns a reference to the XML_Node storred for the phase. | |
| std::string | id () const |
| Return the string id for the phase. | |
| void | setID (std::string id) |
| Set the string id for the phase. | |
| std::string | name () const |
| Return the name of the phase. | |
| void | setName (std::string nm) |
| Sets the string name for the phase. | |
| void | saveState (vector_fp &state) const |
| Save the current internal state of the phase. | |
| void | saveState (int lenstate, doublereal *state) const |
| Write to array 'state' the current internal state. | |
| void | restoreState (const vector_fp &state) |
| Restore a state saved on a previous call to saveState. | |
| void | restoreState (int lenstate, const doublereal *state) |
| Restore the state of the phase from a previously saved state vector. | |
| void | setMoleFractionsByName (compositionMap &xMap) |
| Set the species mole fractions by name. | |
| void | setMoleFractionsByName (const std::string &x) |
| Set the mole fractions of a group of species by name. | |
| void | setMassFractionsByName (compositionMap &yMap) |
| Set the species mass fractions by name. | |
| void | setMassFractionsByName (const std::string &x) |
| Set the species mass fractions by name. | |
| void | setState_TRX (doublereal t, doublereal dens, const doublereal *x) |
| Set the internally storred temperature (K), density, and mole fractions. | |
| void | setState_TRX (doublereal t, doublereal dens, compositionMap &x) |
| Set the internally storred temperature (K), density, and mole fractions. | |
| void | setState_TRY (doublereal t, doublereal dens, const doublereal *y) |
| Set the internally storred temperature (K), density, and mass fractions. | |
| void | setState_TRY (doublereal t, doublereal dens, compositionMap &y) |
| Set the internally storred temperature (K), density, and mass fractions. | |
| void | setState_TNX (doublereal t, doublereal n, const doublereal *x) |
| Set the internally storred temperature (K), molar density (kmol/m^3), and mole fractions. | |
| void | setState_TR (doublereal t, doublereal rho) |
| Set the internally storred temperature (K) and density (kg/m^3). | |
| void | setState_TX (doublereal t, doublereal *x) |
| Set the internally storred temperature (K) and mole fractions. | |
| void | setState_TY (doublereal t, doublereal *y) |
| Set the internally storred temperature (K) and mass fractions. | |
| void | setState_RX (doublereal rho, doublereal *x) |
| Set the density (kg/m^3) and mole fractions. | |
| void | setState_RY (doublereal rho, doublereal *y) |
| Set the density (kg/m^3) and mass fractions. | |
| void | getMolecularWeights (vector_fp &weights) const |
| Copy the vector of molecular weights into vector weights. | |
| void | getMolecularWeights (int iwt, doublereal *weights) const |
| Copy the vector of molecular weights into array weights. | |
| void | getMolecularWeights (doublereal *weights) const |
| Copy the vector of molecular weights into array weights. | |
| const array_fp & | molecularWeights () const |
| Return a const reference to the internal vector of molecular weights. | |
| void | getMoleFractionsByName (compositionMap &x) const |
| Get the mole fractions by name. | |
| doublereal | moleFraction (int k) const |
| Return the mole fraction of a single species. | |
| doublereal | moleFraction (std::string name) const |
| Return the mole fraction of a single species. | |
| doublereal | massFraction (int k) const |
| Return the mass fraction of a single species. | |
| doublereal | massFraction (std::string name) const |
| Return the mass fraction of a single species. | |
| doublereal | chargeDensity () const |
| Charge density [C/m^3]. | |
| int | nDim () const |
| Returns the number of spatial dimensions (1, 2, or 3). | |
| void | setNDim (int ndim) |
| Set the number of spatial dimensions (1, 2, or 3). | |
| virtual void | freezeSpecies () |
| Finished adding species, prepare to use them for calculation of mixture properties. | |
| virtual bool | ready () const |
| True if both elements and species have been frozen. | |
| int | nSpecies () const |
| Returns the number of species in the phase. | |
| doublereal | molecularWeight (int k) const |
Molecular weight of species k. | |
| doublereal | molarMass (int k) const |
Return the Molar mass of species k. | |
| doublereal | charge (int k) const |
| doublereal | nAtoms (int k, int m) const |
Number of atoms of element m in species k. | |
| void | getAtoms (int k, double *atomArray) const |
| Get a vector containing the atomic composition of species k. | |
| void | stateMFChangeCalc (bool forceChange=false) |
| Every time the mole fractions have changed, this routine will increment the stateMFNumber. | |
| int | stateMFNumber () const |
| Return the state number. | |
Utilities | |
| virtual int | eosType () const |
| Equation of state type flag. | |
Molar Thermodynamic Properties of the Solution -------------- | |
| virtual doublereal | enthalpy_mole () const |
| Molar enthalpy. Units: J/kmol. | |
| virtual doublereal | relative_enthalpy () const |
| Excess molar enthalpy of the solution from the mixing process. | |
| virtual doublereal | relative_molal_enthalpy () const |
| Excess molar enthalpy of the solution from the mixing process on a molality basis. | |
| virtual doublereal | intEnergy_mole () const |
| Molar internal energy. Units: J/kmol. | |
| virtual doublereal | entropy_mole () const |
| Molar entropy. Units: J/kmol/K. | |
| virtual doublereal | gibbs_mole () const |
| Molar Gibbs function. Units: J/kmol. | |
| virtual doublereal | cp_mole () const |
| Molar heat capacity at constant pressure. Units: J/kmol/K. | |
| virtual doublereal | cv_mole () const |
| Molar heat capacity at constant volume. Units: J/kmol/K. | |
Activities, Standard States, and Activity Concentrations | |
| virtual void | getActivityConcentrations (doublereal *c) const |
| This method returns an array of generalized activity concentrations. | |
| virtual doublereal | standardConcentration (int k=0) const |
| Return the standard concentration for the kth species. | |
| virtual doublereal | logStandardConc (int k=0) const |
| Returns the natural logarithm of the standard concentration of the kth species. | |
| virtual void | getUnitsStandardConc (double *uA, int k=0, int sizeUA=6) const |
| Returns the units of the standard and generalized concentrations. | |
| virtual void | getActivities (doublereal *ac) const |
| Get the array of non-dimensional activities at the current solution temperature, pressure, and solution concentration. | |
Partial Molar Properties of the Solution ----------------- | |
| virtual void | getChemPotentials (doublereal *mu) const |
| Get the species chemical potentials. Units: J/kmol. | |
| virtual void | getPartialMolarEnthalpies (doublereal *hbar) const |
| Returns an array of partial molar enthalpies for the species in the mixture. | |
| virtual void | getPartialMolarEntropies (doublereal *sbar) const |
| Returns an array of partial molar entropies of the species in the solution. | |
| virtual void | getPartialMolarVolumes (doublereal *vbar) const |
| Return an array of partial molar volumes for the species in the mixture. | |
| virtual void | getPartialMolarCp (doublereal *cpbar) const |
| Return an array of partial molar heat capacities for the species in the mixture. | |
Chemical Equilibrium | |
| virtual void | setToEquilState (const doublereal *lambda_RT) |
| This method is used by the ChemEquil equilibrium solver. | |
Critical state properties. | |
| virtual doublereal | critTemperature () const |
| Critical temperature (K). | |
| virtual doublereal | critPressure () const |
| Critical pressure (Pa). | |
| virtual doublereal | critDensity () const |
| Critical density (kg/m3). | |
Saturation properties. | |
| virtual doublereal | satTemperature (doublereal p) const |
| Return the saturation temperature given the pressure. | |
| virtual doublereal | satPressure (doublereal T) const |
| Get the saturation pressure for a given temperature. | |
| virtual doublereal | vaporFraction () const |
| Return the fraction of vapor at the current conditions. | |
| virtual void | setState_Tsat (doublereal t, doublereal x) |
| Set the state to a saturated system at a particular temperature. | |
| virtual void | setState_Psat (doublereal p, doublereal x) |
| Set the state to a saturated system at a particular pressure. | |
Utilities | |
| void | setpHScale (const int pHscaleType) |
| Set the pH scale, which determines the scale for single-ion activity coefficients. | |
| int | pHScale () const |
| Reports the pH scale, which determines the scale for single-ion activity coefficients. | |
Utilities for Solvent ID and Molality | |
| void | setSolvent (int k) |
| This routine sets the index number of the solvent for the phase. | |
| void | setMoleFSolventMin (doublereal xmolSolventMIN) |
| Sets the minimum mole fraction in the molality formulation. | |
| int | solventIndex () const |
| Returns the solvent index. | |
| doublereal | moleFSolventMin () const |
| Returns the minimum mole fraction in the molality formulation. | |
| void | calcMolalities () const |
| Calculates the molality of all species and stores the result internally. | |
| void | getMolalities (doublereal *const molal) const |
| This function will return the molalities of the species. | |
| void | setMolalities (const doublereal *const molal) |
| Set the molalities of the solutes in a phase. | |
| void | setMolalitiesByName (compositionMap &xMap) |
| Set the molalities of a phase. | |
| void | setMolalitiesByName (const std::string &name) |
| Set the molalities of a phase. | |
Activities, Standard States, and Activity Concentrations | |
| int | activityConvention () const |
| This method returns the activity convention. | |
| void | getActivityCoefficients (doublereal *ac) const |
| Get the array of non-dimensional activity coefficients at the current solution temperature, pressure, and solution concentration. | |
| virtual void | getMolalityActivityCoefficients (doublereal *acMolality) const |
| Get the array of non-dimensional molality based activity coefficients at the current solution temperature, pressure, and solution concentration. | |
| virtual double | osmoticCoefficient () const |
| Calculate the osmotic coefficient. | |
Partial Molar Properties of the Solution | |
| void | getElectrochemPotentials (doublereal *mu) const |
| Get the species electrochemical potentials. | |
Utilities (VPStandardStateTP) | |
| virtual int | standardStateConvention () const |
| This method returns the convention used in specification of the standard state, of which there are currently two, temperature based, and variable pressure based. | |
| virtual void | getdlnActCoeffdlnC (doublereal *dlnActCoeffdlnC) const |
| Get the array of log concentration-like derivatives of the log activity coefficients. | |
Partial Molar Properties of the Solution (VPStandardStateTP) | |
| void | getChemPotentials_RT (doublereal *mu) const |
| Get the array of non-dimensional species chemical potentials These are partial molar Gibbs free energies. | |
Initialization Methods - For Internal use (VPStandardState) | |
| void | setVPSSMgr (VPSSMgr *vp_ptr) |
| set the VPSS Mgr | |
| VPSSMgr * | provideVPSSMgr () |
| Return a pointer to the VPSSMgr for this phase. | |
| void | createInstallPDSS (int k, const XML_Node &s, const XML_Node *phaseNode_ptr) |
| PDSS * | providePDSS (int k) |
| const PDSS * | providePDSS (int k) const |
Information Methods | |
| doublereal | refPressure () const |
| Returns the reference pressure in Pa. | |
| doublereal | minTemp (int k=-1) const |
| Minimum temperature for which the thermodynamic data for the species or phase are valid. | |
| doublereal | Hf298SS (const int k) const |
| Report the 298 K Heat of Formation of the standard state of one species (J kmol-1). | |
| virtual void | modifyOneHf298SS (const int k, const doublereal Hf298New) |
| Modify the value of the 298 K Heat of Formation of one species in the phase (J kmol-1). | |
| doublereal | maxTemp (int k=-1) const |
| Maximum temperature for which the thermodynamic data for the species are valid. | |
Mechanical Properties | |
| virtual void | updateDensity () |
Electric Potential | |
| void | setElectricPotential (doublereal v) |
| Set the electric potential of this phase (V). | |
| doublereal | electricPotential () const |
| Returns the electric potential of this phase (V). | |
Activities, Standard States, and Activity Concentrations | |
| virtual void | getLNActivityCoefficients (doublereal *const lnac) const |
Partial Molar Properties of the Solution | |
| virtual void | getPartialMolarIntEnergies (doublereal *ubar) const |
| Return an array of partial molar internal energies for the species in the mixture. | |
Thermodynamic Values for the Species Reference States | |
| virtual void | getIntEnergy_RT_ref (doublereal *urt) const |
| Returns the vector of nondimensional internal Energies of the reference state at the current temperature of the solution and the reference pressure for each species. | |
| virtual void | setReferenceComposition (const doublereal *const x) |
| Sets the reference composition. | |
| virtual void | getReferenceComposition (doublereal *const x) const |
| Gets the reference composition. | |
Specific Properties | |
| doublereal | enthalpy_mass () const |
| Specific enthalpy. | |
| doublereal | intEnergy_mass () const |
| Specific internal energy. | |
| doublereal | entropy_mass () const |
| Specific entropy. | |
| doublereal | gibbs_mass () const |
| Specific Gibbs function. | |
| doublereal | cp_mass () const |
| Specific heat at constant pressure. | |
| doublereal | cv_mass () const |
| Specific heat at constant volume. | |
Setting the State | |
| void | setState_TPX (doublereal t, doublereal p, const doublereal *x) |
| Set the temperature (K), pressure (Pa), and mole fractions. | |
| void | setState_TPX (doublereal t, doublereal p, compositionMap &x) |
| Set the temperature (K), pressure (Pa), and mole fractions. | |
| void | setState_TPX (doublereal t, doublereal p, const std::string &x) |
| Set the temperature (K), pressure (Pa), and mole fractions. | |
| void | setState_TPY (doublereal t, doublereal p, const doublereal *y) |
| Set the internally storred temperature (K), pressure (Pa), and mass fractions of the phase. | |
| void | setState_TPY (doublereal t, doublereal p, compositionMap &y) |
| Set the internally storred temperature (K), pressure (Pa), and mass fractions of the phase. | |
| void | setState_TPY (doublereal t, doublereal p, const std::string &y) |
| Set the internally storred temperature (K), pressure (Pa), and mass fractions of the phase. | |
| void | setState_PX (doublereal p, doublereal *x) |
| Set the pressure (Pa) and mole fractions. | |
| void | setState_PY (doublereal p, doublereal *y) |
| Set the internally storred pressure (Pa) and mass fractions. | |
| virtual void | setState_HP (doublereal h, doublereal p, doublereal tol=1.e-4) |
| Set the internally storred specific enthalpy (J/kg) and pressure (Pa) of the phase. | |
| virtual void | setState_UV (doublereal u, doublereal v, doublereal tol=1.e-4) |
| Set the specific internal energy (J/kg) and specific volume (m^3/kg). | |
| virtual void | setState_SP (doublereal s, doublereal p, doublereal tol=1.e-4) |
| Set the specific entropy (J/kg/K) and pressure (Pa). | |
| virtual void | setState_SV (doublereal s, doublereal v, doublereal tol=1.e-4) |
| Set the specific entropy (J/kg/K) and specific volume (m^3/kg). | |
Chemical Equilibrium | |
| void | setElementPotentials (const vector_fp &lambda) |
| Stores the element potentials in the ThermoPhase object. | |
| bool | getElementPotentials (doublereal *lambda) const |
| Returns the element potentials storred in the ThermoPhase object. | |
Initialization Methods - For Internal Use (ThermoPhase) | |
| void | saveSpeciesData (const int k, const XML_Node *const data) |
| Store a reference pointer to the XML tree containing the species data for this phase. | |
| const std::vector< const XML_Node * > & | speciesData () const |
| Return a pointer to the vector of XML nodes containing the species data for this phase. | |
| void | setSpeciesThermo (SpeciesThermo *spthermo) |
| Install a species thermodynamic property manager. | |
| virtual void | initThermoFile (std::string inputFile, std::string id) |
| int | index () const |
| void | setIndex (int m) |
Element Information | |
| std::string | elementName (int m) const |
| Name of the element with index m. | |
| int | elementIndex (std::string name) const |
| Index of element named 'name'. | |
| doublereal | atomicWeight (int m) const |
| Atomic weight of element m. | |
| doublereal | entropyElement298 (int m) const |
| Entropy of the element in its standard state at 298 K and 1 bar. | |
| int | atomicNumber (int m) const |
| Atomic number of element m. | |
| const std::vector< std::string > & | elementNames () const |
| Return a read-only reference to the vector of element names. | |
| const vector_fp & | atomicWeights () const |
| Return a read-only reference to the vector of atomic weights. | |
| int | nElements () const |
| Number of elements. | |
Adding Elements and Species | |
| void | addElement (const std::string &symbol, doublereal weight) |
| Add an element. | |
| void | addElement (const XML_Node &e) |
| Add an element from an XML specification. | |
| void | addUniqueElement (const std::string &symbol, doublereal weight, int atomicNumber=0, doublereal entropy298=ENTROPY298_UNKNOWN) |
| Add an element, checking for uniqueness. | |
| void | addUniqueElement (const XML_Node &e) |
| Adde an element, checking for uniqueness. | |
| void | addElementsFromXML (const XML_Node &phase) |
| Add all elements referenced in an XML_Node tree. | |
| void | freezeElements () |
| Prohibit addition of more elements, and prepare to add species. | |
| bool | elementsFrozen () |
| True if freezeElements has been called. | |
Adding Species | |
| void | addSpecies (const std::string &name, const doublereal *comp, doublereal charge=0.0, doublereal size=1.0) |
| void | addUniqueSpecies (const std::string &name, const doublereal *comp, doublereal charge=0.0, doublereal size=1.0) |
| Add a species to the phase, checking for uniqueness of the name. | |
| int | speciesIndex (std::string name) const |
| Index of species named 'name'. | |
| std::string | speciesName (int k) const |
| Name of the species with index k. | |
| const std::vector< std::string > & | speciesNames () const |
| Return a const referernce to the vector of species names. | |
| doublereal | size (int k) const |
| This routine returns the size of species k. | |
| bool | speciesFrozen () |
| True if freezeSpecies has been called. | |
| void | clear () |
| Remove all elements and species. | |
Composition | |
| void | getMoleFractions (doublereal *const x) const |
| Get the species mole fraction vector. | |
| virtual void | setMoleFractions (const doublereal *const x) |
| Set the mole fractions to the specified values, and then normalize them so that they sum to 1.0. | |
| virtual void | setMoleFractions_NoNorm (const doublereal *const x) |
| Set the mole fractions to the specified values without normalizing. | |
| void | getMassFractions (doublereal *const y) const |
| Get the species mass fractions. | |
| virtual void | setMassFractions (const doublereal *const y) |
| Set the mass fractions to the specified values, and then normalize them so that they sum to 1.0. | |
| virtual void | setMassFractions_NoNorm (const doublereal *const y) |
| Set the mass fractions to the specified values without normalizing. | |
| void | getConcentrations (doublereal *const c) const |
| Get the species concentrations (kmol/m^3). | |
| doublereal | concentration (const int k) const |
| Concentration of species k. | |
| virtual void | setConcentrations (const doublereal *const conc) |
| Set the concentrations to the specified values within the phase. | |
| const doublereal * | massFractions () const |
| Returns a read-only pointer to the start of the massFraction array. | |
| const doublereal * | moleFractdivMMW () const |
| Returns a read-only pointer to the start of the moleFraction/MW array. | |
Mean Properties | |
| doublereal | mean_X (const doublereal *const Q) const |
| Evaluate the mole-fraction-weighted mean of Q:
| |
| doublereal | mean_Y (const doublereal *const Q) const |
| Evaluate the mass-fraction-weighted mean of Q:
| |
| doublereal | meanMolecularWeight () const |
| The mean molecular weight. | |
| doublereal | sum_xlogx () const |
Evaluate 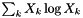 . . | |
| doublereal | sum_xlogQ (doublereal *const Q) const |
Evaluate 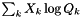 . . | |
Thermodynamic Properties | |
Class State only stores enough thermodynamic data to specify the state. In addition to composition information, it stores the temperature and mass density. | |
| doublereal | temperature () const |
| Temperature (K). | |
| doublereal | molarDensity () const |
| Molar density (kmol/m^3). | |
Public Attributes | |
| int | m_form_A_Debye |
| Form of the constant outside the Debye-Huckel term called A. | |
| int | m_debugCalc |
Protected Member Functions | |
| void | init (const array_fp &mw) |
| void | setMolecularWeight (const int k, const double mw) |
| Set the molecular weight of a single species to a given value. | |
Protected Attributes | |
| int | m_indexSolvent |
| Index of the solvent. | |
| int | m_pHScalingType |
| Scaling to be used for output of single-ion species activity coefficients. | |
| int | m_indexCLM |
| Index of the phScale species. | |
| doublereal | m_weightSolvent |
| Molecular weight of the Solvent. | |
| doublereal | m_xmolSolventMIN |
| doublereal | m_Mnaught |
| This is the multiplication factor that goes inside log expressions involving the molalities of species. | |
| vector_fp | m_molalities |
| Current value of the molalities of the species in the phase. | |
| doublereal | m_Pcurrent |
| Current value of the pressure - state variable. | |
| doublereal | m_Tlast_ss |
| The last temperature at which the standard statethermodynamic properties were calculated at. | |
| doublereal | m_Plast_ss |
| The last pressure at which the Standard State thermodynamic properties were calculated at. | |
| doublereal | m_P0 |
| VPSSMgr * | m_VPSS_ptr |
| Pointer to the VPSS manager that calculates all of the standard state info efficiently. | |
| std::vector< PDSS * > | m_PDSS_storage |
| Storage for the PDSS objects for the species. | |
| SpeciesThermo * | m_spthermo |
| Pointer to the calculation manager for species reference-state thermodynamic properties. | |
| std::vector< const XML_Node * > | m_speciesData |
| Vector of pointers to the species databases. | |
| int | m_index |
| Index number of the phase. | |
| doublereal | m_phi |
| Storred value of the electric potential for this phase. | |
| vector_fp | m_lambdaRRT |
| Vector of element potentials. | |
| bool | m_hasElementPotentials |
| Boolean indicating whether there is a valid set of saved element potentials for this phase. | |
| bool | m_chargeNeutralityNecessary |
| Boolean indicating whether a charge neutrality condition is a necessity. | |
| int | m_ssConvention |
| Contains the standard state convention. | |
| std::vector< doublereal > | xMol_Ref |
| Reference Mole Fraction Composition. | |
| int | m_kk |
| m_kk = Number of species in the phase. | |
| int | m_ndim |
| m_ndim is the dimensionality of the phase. | |
| vector_fp | m_weight |
| Vector of molecular weights of the species. | |
| bool | m_speciesFrozen |
| Boolean indicating whether the number of species has been frozen. | |
| Elements * | m_Elements |
| std::vector< std::string > | m_speciesNames |
| Vector of the species names. | |
| vector_fp | m_speciesComp |
| Atomic composition of the species. | |
| vector_fp | m_speciesCharge |
| m_speciesCharge: Vector of species charges length = m_kk | |
| vector_fp | m_speciesSize |
| m_speciesSize(): Vector of species sizes. | |
Private Member Functions | |
| void | s_updateScaling_pHScaling () const |
| Apply the current phScale to a set of activity Coefficients. | |
| void | s_updateScaling_pHScaling_dT () const |
| Apply the current phScale to a set of derivatives of the activity Coefficients wrt temperature. | |
| void | s_updateScaling_pHScaling_dT2 () const |
| Apply the current phScale to a set of 2nd derivatives of the activity Coefficients wrt temperature. | |
| void | s_updateScaling_pHScaling_dP () const |
| Apply the current phScale to a set of derivatives of the activity Coefficients wrt pressure. | |
| doublereal | s_NBS_CLM_lnMolalityActCoeff () const |
| Calculate the Chlorine activity coefficient on the NBS scale. | |
| doublereal | s_NBS_CLM_dlnMolalityActCoeff_dT () const |
| Calculate the temperature derivative of the Chlorine activity coefficient on the NBS scale. | |
| doublereal | s_NBS_CLM_d2lnMolalityActCoeff_dT2 () const |
| Calculate the second temperature derivative of the Chlorine activity coefficient on the NBS scale. | |
| doublereal | s_NBS_CLM_dlnMolalityActCoeff_dP () const |
| Calculate the pressure derivative of the Chlorine activity coefficient. | |
| doublereal | err (std::string msg) const |
| Local error routine. | |
| void | initLengths () |
| Initialize all of the species - dependent lengths in the object. | |
| virtual void | applyphScale (doublereal *acMolality) const |
| Apply the current phScale to a set of activity Coefficients or activities. | |
| void | s_update_lnMolalityActCoeff () const |
| Calcuate the natural log of the molality-based activity coefficients. | |
| void | s_update_dlnMolalityActCoeff_dT () const |
| This function calculates the temperature derivative of the. | |
| void | s_update_d2lnMolalityActCoeff_dT2 () const |
| This function calculates the temperature second derivative of the natural logarithm of the molality activity coefficients. | |
| void | s_update_dlnMolalityActCoeff_dP () const |
| This function calculates the pressure derivative of the natural logarithm of the molality activity coefficients. | |
| void | s_updateIMS_lnMolalityActCoeff () const |
| This function will be called to update the internally storred natural logarithm of the molality activity coefficients. | |
| void | s_updatePitzer_lnMolalityActCoeff () const |
| This function does the main pitzer coefficient calculation. | |
| void | s_updatePitzer_dlnMolalityActCoeff_dT () const |
| Calculates the temperature derivative of the natural logarithm of the molality activity coefficients. | |
| void | s_updatePitzer_d2lnMolalityActCoeff_dT2 () const |
| This function calculates the temperature second derivative of the natural logarithm of the molality activity coefficients. | |
| void | s_updatePitzer_dlnMolalityActCoeff_dP () const |
| Calculates the Pressure derivative of the natural logarithm of the molality activity coefficients. | |
| void | s_updatePitzer_CoeffWRTemp (int doDerivs=2) const |
| Calculates the Pitzer coefficients' dependence on the temperature. | |
| void | calc_lambdas (double is) const |
| Calculate the lambda interactions. | |
| void | calc_thetas (int z1, int z2, double *etheta, double *etheta_prime) const |
| Calculate etheta and etheta_prime. | |
| void | counterIJ_setup () const |
| Set up a counter variable for keeping track of symmetric binary interactactions amongst the solute species. | |
| void | calcMolalitiesCropped () const |
| Calculate the cropped molalities. | |
| void | readXMLBinarySalt (XML_Node &BinSalt) |
| Process an XML node called "binarySaltParameters". | |
| void | readXMLThetaAnion (XML_Node &BinSalt) |
| Process an XML node called "thetaAnion". | |
| void | readXMLThetaCation (XML_Node &BinSalt) |
| Process an XML node called "thetaCation". | |
| void | readXMLPsiCommonAnion (XML_Node &BinSalt) |
| Process an XML node called "psiCommonAnion". | |
| void | readXMLPsiCommonCation (XML_Node &BinSalt) |
| Process an XML node called "psiCommonCation". | |
| void | readXMLLambdaNeutral (XML_Node &BinSalt) |
| Process an XML node called "lambdaNeutral". | |
| void | readXMLMunnnNeutral (XML_Node &BinSalt) |
| Process an XML node called "MunnnNeutral". | |
| void | readXMLZetaCation (const XML_Node &BinSalt) |
| Process an XML node called "zetaCation". | |
| void | readXMLCroppingCoefficients (const XML_Node &acNode) |
| Process an XML node called "croppingCoefficients" for the cropping coefficients values. | |
| void | calcIMSCutoffParams_ () |
| Precalculate the IMS Cutoff parameters for typeCutoff = 2. | |
| void | calcMCCutoffParams_ () |
| Calculate molality cut-off parameters. | |
Static Private Member Functions | |
| static int | interp_est (std::string estString) |
| Utility function to assign an integer value from a string for the ElectrolyteSpeciesType field. | |
Private Attributes | |
| int | m_formPitzer |
| This is the form of the Pitzer parameterization used in this model. | |
| int | m_formPitzerTemp |
| This is the form of the temperature dependence of Pitzer parameterization used in the model. | |
| int | m_formGC |
| Format for the generalized concentration: | |
| vector_int | m_electrolyteSpeciesType |
| Vector containing the electrolyte species type. | |
| array_fp | m_Aionic |
Species molar volumes 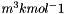 -> m_speciesSize in Constituents.h. -> m_speciesSize in Constituents.h. | |
| double | m_IionicMolality |
| Current value of the ionic strength on the molality scale Associated Salts, if present in the mechanism, don't contribute to the value of the ionic strength in this version of the Ionic strength. | |
| double | m_maxIionicStrength |
| Maximum value of the ionic strength allowed in the calculation of the activity coefficients. | |
| double | m_TempPitzerRef |
| Reference Temperature for the Pitzer formulations. | |
| double | m_IionicMolalityStoich |
| Stoichiometric ionic strength on the molality scale. | |
| double | m_A_Debye |
| A_Debye -> this expression appears on the top of the ln actCoeff term in the general Debye-Huckel expression It depends on temperature. | |
| PDSS * | m_waterSS |
| Water standard state calculator. | |
| double | m_densWaterSS |
| density of standard-state water | |
| WaterProps * | m_waterProps |
| Pointer to the water property calculator. | |
| vector_fp | m_expg0_RT |
| Vector containing the species reference exp(-G/RT) functions at T = m_tlast. | |
| vector_fp | m_pe |
| Vector of potential energies for the species. | |
| vector_fp | m_pp |
| Temporary array used in equilibrium calculations. | |
| vector_fp | m_tmpV |
| vector of size m_kk, used as a temporary holding area. | |
| vector_fp | m_speciesCharge_Stoich |
| Stoichiometric species charge -> This is for calculations of the ionic strength which ignore ion-ion pairing into neutral molecules. | |
| vector_fp | m_Beta0MX_ij |
| Array of 2D data used in the Pitzer/HMW formulation. | |
| vector_fp | m_Beta0MX_ij_L |
| Derivative of Beta0_ij[i][j] wrt T. | |
| vector_fp | m_Beta0MX_ij_LL |
| Derivative of Beta0_ij[i][j] wrt TT. | |
| vector_fp | m_Beta0MX_ij_P |
| Derivative of Beta0_ij[i][j] wrt P. | |
| Array2D | m_Beta0MX_ij_coeff |
| Array of coefficients for Beta0, a variable in Pitzer's papers. | |
| vector_fp | m_Beta1MX_ij |
| vector_fp | m_Beta1MX_ij_L |
| Derivative of Beta1_ij[i][j] wrt T. | |
| vector_fp | m_Beta1MX_ij_LL |
| Derivative of Beta1_ij[i][j] wrt TT. | |
| vector_fp | m_Beta1MX_ij_P |
| Derivative of Beta1_ij[i][j] wrt P. | |
| Array2D | m_Beta1MX_ij_coeff |
| Array of coefficients for Beta1, a variable in Pitzer's papers. | |
| vector_fp | m_Beta2MX_ij |
| Array of 2D data used in the Pitzer/HMW formulation. | |
| vector_fp | m_Beta2MX_ij_L |
| Derivative of Beta2_ij[i][j] wrt T. | |
| vector_fp | m_Beta2MX_ij_LL |
| Derivative of Beta2_ij[i][j] wrt TT. | |
| vector_fp | m_Beta2MX_ij_P |
| Derivative of Beta2_ij[i][j] wrt P. | |
| Array2D | m_Beta2MX_ij_coeff |
| Array of coefficients for Beta2, a variable in Pitzer's papers. | |
| vector_fp | m_Alpha1MX_ij |
| Array of 2D data used in the Pitzer/HMW formulation. | |
| vector_fp | m_Alpha2MX_ij |
| Array of 2D data used in the Pitzer/HMW formulation. | |
| vector_fp | m_CphiMX_ij |
| Array of 2D data used in the Pitzer/HMW formulation. | |
| vector_fp | m_CphiMX_ij_L |
| Derivative of Cphi_ij[i][j] wrt T. | |
| vector_fp | m_CphiMX_ij_LL |
| Derivative of Cphi_ij[i][j] wrt TT. | |
| vector_fp | m_CphiMX_ij_P |
| Derivative of Cphi_ij[i][j] wrt P. | |
| Array2D | m_CphiMX_ij_coeff |
| Array of coefficients for CphiMX, a parameter in the activity coefficient formulation. | |
| vector_fp | m_Theta_ij |
| Array of 2D data for Theta_ij[i][j] in the Pitzer/HMW formulation. | |
| vector_fp | m_Theta_ij_L |
| Derivative of Theta_ij[i][j] wrt T. | |
| vector_fp | m_Theta_ij_LL |
| Derivative of Theta_ij[i][j] wrt TT. | |
| vector_fp | m_Theta_ij_P |
| Derivative of Theta_ij[i][j] wrt P. | |
| Array2D | m_Theta_ij_coeff |
| Array of coefficients for Theta_ij[i][j] in the Pitzer/HMW formulation. | |
| vector_fp | m_Psi_ijk |
| Array of 3D data used in the Pitzer/HMW formulation. | |
| vector_fp | m_Psi_ijk_L |
| Derivitive of Psi_ijk[n] wrt T. | |
| vector_fp | m_Psi_ijk_LL |
| Derivitive of Psi_ijk[n] wrt TT. | |
| vector_fp | m_Psi_ijk_P |
| Derivitive of Psi_ijk[n] wrt P. | |
| Array2D | m_Psi_ijk_coeff |
| Array of coefficients for Psi_ijk[n] in the Pitzer/HMW formulation. | |
| Array2D | m_Lambda_nj |
| Lambda coefficient for the ij interaction. | |
| Array2D | m_Lambda_nj_L |
| Derivative of Lambda_nj[i][j] wrt T. see m_Lambda_ij. | |
| Array2D | m_Lambda_nj_LL |
| Derivative of Lambda_nj[i][j] wrt TT. | |
| Array2D | m_Lambda_nj_P |
| Derivative of Lambda_nj[i][j] wrt P. | |
| Array2D | m_Lambda_nj_coeff |
| Array of coefficients for Lambda_nj[i][j] in the Pitzer/HMW formulation. | |
| vector_fp | m_Mu_nnn |
| Mu coefficient for the self-ternary neutral coefficient. | |
| vector_fp | m_Mu_nnn_L |
| Mu coefficient temperature derivative for the self-ternary neutral coefficient. | |
| vector_fp | m_Mu_nnn_LL |
| Mu coefficient 2nd temperature derivative for the self-ternary neutral coefficient. | |
| vector_fp | m_Mu_nnn_P |
| Mu coefficient pressure derivative for the self-ternary neutral coefficient. | |
| Array2D | m_Mu_nnn_coeff |
| Array of coefficients form_Mu_nnn term. | |
| vector_fp | m_lnActCoeffMolal_Scaled |
| Logarithm of the activity coefficients on the molality scale. | |
| vector_fp | m_lnActCoeffMolal_Unscaled |
| Logarithm of the activity coefficients on the molality. | |
| vector_fp | m_dlnActCoeffMolaldT_Scaled |
| Derivative of the Logarithm of the activity coefficients on the molality scale wrt T. | |
| vector_fp | m_dlnActCoeffMolaldT_Unscaled |
| Derivative of the Logarithm of the activity coefficients on the molality scale wrt T. | |
| vector_fp | m_d2lnActCoeffMolaldT2_Scaled |
| Derivative of the Logarithm of the activity coefficients on the molality scale wrt TT. | |
| vector_fp | m_d2lnActCoeffMolaldT2_Unscaled |
| Derivative of the Logarithm of the activity coefficients on the molality. | |
| vector_fp | m_dlnActCoeffMolaldP_Scaled |
| Derivative of the Logarithm of the activity coefficients on the molality scale wrt P. | |
| vector_fp | m_dlnActCoeffMolaldP_Unscaled |
| Derivative of the Logarithm of the activity coefficients on the molality scale wrt P. | |
| vector_fp | m_molalitiesCropped |
| Cropped and modified values of the molalities used in activity coefficient calculations. | |
| bool | m_molalitiesAreCropped |
| Boolean indicating whether the molalities are cropped or are modified. | |
| array_int | m_CounterIJ |
| a counter variable for keeping track of symmetric binary interactions amongst the solute species. | |
| double | elambda [17] |
| This is elambda, MEC. | |
| double | elambda1 [17] |
| This is elambda1, MEC. | |
| vector_fp | m_gfunc_IJ |
| Various temporary arrays used in the calculation of the Pitzer activity coefficents. | |
| vector_fp | m_g2func_IJ |
| This is the value of g2(x2) in Pitzer's papers. | |
| vector_fp | m_hfunc_IJ |
| hfunc, was called gprime in Pitzer's paper. | |
| vector_fp | m_h2func_IJ |
| hfunc2, was called gprime in Pitzer's paper. | |
| vector_fp | m_BMX_IJ |
| Intermediate variable called BMX in Pitzer's paper This is the basic cation - anion interaction. | |
| vector_fp | m_BMX_IJ_L |
| Derivative of BMX_IJ wrt T. | |
| vector_fp | m_BMX_IJ_LL |
| Derivative of BMX_IJ wrt TT. | |
| vector_fp | m_BMX_IJ_P |
| Derivative of BMX_IJ wrt P. | |
| vector_fp | m_BprimeMX_IJ |
| Intermediate variable called BprimeMX in Pitzer's paper. | |
| vector_fp | m_BprimeMX_IJ_L |
| Derivative of BprimeMX wrt T. | |
| vector_fp | m_BprimeMX_IJ_LL |
| Derivative of BprimeMX wrt TT. | |
| vector_fp | m_BprimeMX_IJ_P |
| Derivative of BprimeMX wrt P. | |
| vector_fp | m_BphiMX_IJ |
| Intermediate variable called BphiMX in Pitzer's paper. | |
| vector_fp | m_BphiMX_IJ_L |
| Derivative of BphiMX_IJ wrt T. | |
| vector_fp | m_BphiMX_IJ_LL |
| Derivative of BphiMX_IJ wrt TT. | |
| vector_fp | m_BphiMX_IJ_P |
| Derivative of BphiMX_IJ wrt P. | |
| vector_fp | m_Phi_IJ |
| Intermediate variable called Phi in Pitzer's paper. | |
| vector_fp | m_Phi_IJ_L |
| Derivative of m_Phi_IJ wrt T. | |
| vector_fp | m_Phi_IJ_LL |
| Derivative of m_Phi_IJ wrt TT. | |
| vector_fp | m_Phi_IJ_P |
| Derivative of m_Phi_IJ wrt P. | |
| vector_fp | m_Phiprime_IJ |
| Intermediate variable called Phiprime in Pitzer's paper. | |
| vector_fp | m_PhiPhi_IJ |
| Intermediate variable called PhiPhi in Pitzer's paper. | |
| vector_fp | m_PhiPhi_IJ_L |
| Derivative of m_PhiPhi_IJ wrt T. | |
| vector_fp | m_PhiPhi_IJ_LL |
| Derivative of m_PhiPhi_IJ wrt TT. | |
| vector_fp | m_PhiPhi_IJ_P |
| Derivative of m_PhiPhi_IJ wrt P. | |
| vector_fp | m_CMX_IJ |
| Intermediate variable called CMX in Pitzer's paper. | |
| vector_fp | m_CMX_IJ_L |
| Derivative of m_CMX_IJ wrt T. | |
| vector_fp | m_CMX_IJ_LL |
| Derivative of m_CMX_IJ wrt TT. | |
| vector_fp | m_CMX_IJ_P |
| Derivative of m_CMX_IJ wrt P. | |
| vector_fp | m_gamma_tmp |
| Intermediate storage of the activity coefficient itself. | |
| vector_fp | IMS_lnActCoeffMolal_ |
| Logarithm of the molal activity coefficients. | |
| int | IMS_typeCutoff_ |
| IMS Cutoff type. | |
| doublereal | IMS_X_o_cutoff_ |
| value of the solute mole fraction that centers the cutoff polynomials for the cutoff =1 process; | |
| doublereal | IMS_gamma_o_min_ |
| gamma_o value for the cutoff process at the zero solvent point | |
| doublereal | IMS_gamma_k_min_ |
| gamma_k minimun for the cutoff process at the zero solvent point | |
| doublereal | IMS_cCut_ |
| Parameter in the polyExp cutoff treatment having to do with rate of exp decay. | |
| doublereal | IMS_slopefCut_ |
| Parameter in the polyExp cutoff treatment. | |
| doublereal | IMS_dfCut_ |
| Parameter in the polyExp cutoff treatment having to do with rate of exp decay. | |
| doublereal | IMS_efCut_ |
| Parameter in the polyExp cutoff treatment having to do with rate of exp decay. | |
| doublereal | IMS_afCut_ |
| Parameter in the polyExp cutoff treatment having to do with rate of exp decay. | |
| doublereal | IMS_bfCut_ |
| Parameter in the polyExp cutoff treatment having to do with rate of exp decay. | |
| doublereal | IMS_slopegCut_ |
| Parameter in the polyExp cutoff treatment. | |
| doublereal | IMS_dgCut_ |
| Parameter in the polyExp cutoff treatment having to do with rate of exp decay. | |
| doublereal | IMS_egCut_ |
| Parameter in the polyExp cutoff treatment having to do with rate of exp decay. | |
| doublereal | IMS_agCut_ |
| Parameter in the polyExp cutoff treatment having to do with rate of exp decay. | |
| doublereal | IMS_bgCut_ |
| Parameter in the polyExp cutoff treatment having to do with rate of exp decay. | |
| doublereal | MC_X_o_cutoff_ |
| value of the solvent mole fraction that centers the cutoff polynomials for the cutoff =1 process; | |
| doublereal | MC_X_o_min_ |
| gamma_o value for the cutoff process at the zero solvent point | |
| doublereal | MC_slopepCut_ |
| Parameter in the Molality Exp cutoff treatment. | |
| doublereal | MC_dpCut_ |
| Parameter in the Molality Exp cutoff treatment. | |
| doublereal | MC_epCut_ |
| Parameter in the Molality Exp cutoff treatment. | |
| doublereal | MC_apCut_ |
| Parameter in the Molality Exp cutoff treatment. | |
| doublereal | MC_bpCut_ |
| Parameter in the Molality Exp cutoff treatment. | |
| doublereal | MC_cpCut_ |
| Parameter in the Molality Exp cutoff treatment. | |
| doublereal | CROP_ln_gamma_o_min |
| Parameter in the Molality Exp cutoff treatment. | |
| doublereal | CROP_ln_gamma_o_max |
| Parameter in the Molality Exp cutoff treatment. | |
| doublereal | CROP_ln_gamma_k_min |
| Parameter in the Molality Exp cutoff treatment. | |
| doublereal | CROP_ln_gamma_k_max |
| Parameter in the Molality Exp cutoff treatment. | |
| std::vector< int > | CROP_speciesCropped_ |
| This is a boolean-type vector indicating whether a species's activity coefficient is in the cropped regime. | |
Mechanical Equation of State Properties --------------------- | |
|
| |
| virtual doublereal | pressure () const |
| In this equation of state implementation, the density is a function only of the mole fractions. | |
| virtual void | setPressure (doublereal p) |
| Set the internally storred pressure (Pa) at constant temperature and composition. | |
| virtual doublereal | density () const |
| Returns the current value of the density. | |
| void | setDensity (const doublereal rho) |
| Set the internally storred density (kg/m^3) of the phase. | |
| void | setMolarDensity (const doublereal conc) |
| Set the internally storred molar density (kmol/m^3) for the phase. | |
| virtual void | setTemperature (const doublereal temp) |
| Set the temperature (K). | |
| virtual void | setState_TP (doublereal t, doublereal p) |
| Set the temperature (K) and pressure (Pa). | |
| virtual doublereal | isothermalCompressibility () const |
| The isothermal compressibility. | |
| virtual doublereal | thermalExpansionCoeff () const |
| The thermal expansion coefficient. | |
| void | calcDensity () |
| Calculate the density of the mixture using the partial molar volumes and mole fractions as input. | |
Properties of the Standard State of the Species in the Solution | |
|
Within VPStandardStateTP, these properties are calculated via a common routine, _updateStandardStateThermo(), which must be overloaded in inherited objects. The values are cached within this object, and are not recalculated unless the temperature or pressure changes. | |
| virtual void | getStandardChemPotentials (doublereal *mu) const |
| Get the array of chemical potentials at unit activity. | |
| virtual void | getEnthalpy_RT (doublereal *hrt) const |
| Get the nondimensional Enthalpy functions for the species at their standard states at the current T and P of the solution. | |
| virtual void | getEntropy_R (doublereal *sr) const |
| Get the array of nondimensional Enthalpy functions for the standard state species at the current T and P of the solution. | |
| virtual void | getGibbs_RT (doublereal *grt) const |
| Get the nondimensional Gibbs functions for the species at their standard states of solution at the current T and P of the solution. | |
| void | getPureGibbs (doublereal *gpure) const |
| Get the nondimensional Gibbs functions for the standard state of the species at the current T and P. | |
| virtual void | getIntEnergy_RT (doublereal *urt) const |
| Returns the vector of nondimensional internal Energies of the standard state at the current temperature and pressure of the solution for each species. | |
| virtual void | getCp_R (doublereal *cpr) const |
| Get the nondimensional Heat Capacities at constant pressure for the standard state of the species at the current T and P. | |
| virtual void | getStandardVolumes (doublereal *vol) const |
| Get the molar volumes of each species in their standard states at the current T and P of the solution. | |
| virtual void | updateStandardStateThermo () const |
| Updates the standard state thermodynamic functions at the current T and P of the solution. | |
| virtual void | _updateStandardStateThermo () const |
| Updates the standard state thermodynamic functions at the current T and P of the solution. | |
Thermodynamic Values for the Species Reference States (VPStandardStateTP) | |
|
| |
| virtual void | getEnthalpy_RT_ref (doublereal *hrt) const |
| Returns the vector of nondimensional enthalpies of the reference state at the current temperature of the solution and the reference pressure for the species. | |
| virtual void | getGibbs_RT_ref (doublereal *grt) const |
| Returns the vector of nondimensional Gibbs free energies of the reference state at the current temperature of the solution and the reference pressure for the species. | |
| virtual void | getGibbs_ref (doublereal *g) const |
| virtual void | getEntropy_R_ref (doublereal *er) const |
| virtual void | getCp_R_ref (doublereal *cprt) const |
| virtual void | getStandardVolumes_ref (doublereal *vol) const |
| Get the molar volumes of the species reference states at the current T and P_ref of the solution. | |
| const vector_fp & | Gibbs_RT_ref () const |
Detailed Description
Class HMWSoln represents a dilute or concentrated liquid electrolyte phase which obeys the Pitzer formulation for nonideality.
As a prerequisite to the specification of thermodynamic quantities, The concentrations of the ionic species are assumed to obey the electroneutrality condition.
Specification of Species Standard State Properties
The solvent is assumed to be liquid water. A real model for liquid water (IAPWS 1995 formulation) is used as its standard state. All standard state properties for the solvent are based on this real model for water, and involve function calls to the object that handles the real water model, Cantera::WaterPropsIAPWS.
The standard states for solutes are on the unit molality basis. Therefore, in the documentation below, the normal 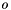 superscript is replaced with the
superscript is replaced with the  symbol. The reference state symbol is now
symbol. The reference state symbol is now 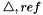 .
.
It is assumed that the reference state thermodynamics may be obtained by a pointer to a populated species thermodynamic property manager class (see ThermoPhase::m_spthermo). How to relate pressure changes to the reference state thermodynamics is resolved at this level.
For solutes that rely on ThermoPhase::m_spthermo, are assumed to have an incompressible standard state mechanical property. In other words, the molar volumes are independent of temperature and pressure.
For these incompressible, standard states, the molar internal energy is independent of pressure. Since the thermodynamic properties are specified by giving the standard-state enthalpy, the term 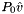 is subtracted from the specified molar enthalpy to compute the molar internal energy. The entropy is assumed to be independent of the pressure.
is subtracted from the specified molar enthalpy to compute the molar internal energy. The entropy is assumed to be independent of the pressure.
The enthalpy function is given by the following relation.
![\[ \raggedright h^\triangle_k(T,P) = h^{\triangle,ref}_k(T) + \tilde{v}_k \left( P - P_{ref} \right) \]](form_110.png)
For an incompressible, stoichiometric substance, the molar internal energy is independent of pressure. Since the thermodynamic properties are specified by giving the standard-state enthalpy, the term 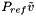 is subtracted from the specified reference molar enthalpy to compute the molar internal energy.
is subtracted from the specified reference molar enthalpy to compute the molar internal energy.
![\[ u^\triangle_k(T,P) = h^{\triangle,ref}_k(T) - P_{ref} \tilde{v}_k \]](form_111.png)
The solute standard state heat capacity and entropy are independent of pressure. The solute standard state gibbs free energy is obtained from the enthalpy and entropy functions.
The vector Constituents::m_speciesSize[] is used to hold the base values of species sizes. These are defined as the molar volumes of species at infinite dilution at 300 K and 1 atm of water. m_speciesSize are calculated during the initialization of the HMWSoln object and are then not touched.
The current model assumes that an incompressible molar volume for all solutes. The molar volume for the water solvent, however, is obtained from a pure water equation of state, waterSS. Therefore, the water standard state varies with both T and P. It is an error to request standard state water properties at a T and P where the water phase is not a stable phase, i.e., beyond its spinodal curve.
Specification of Solution Thermodynamic Properties
Chemical potentials of the solutes, 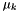 , and the solvent,
, and the solvent, 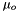 , which are based on the molality form, have the following general format:
, which are based on the molality form, have the following general format:
![\[ \mu_k = \mu^{\triangle}_k(T,P) + R T ln(\gamma_k^{\triangle} \frac{m_k}{m^\triangle}) \]](form_30.png)
![\[ \mu_o = \mu^o_o(T,P) + RT ln(a_o) \]](form_31.png)
where 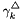 is the molality based activity coefficient for species
is the molality based activity coefficient for species 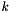 .
.
Individual activity coefficients of ions can not be independently measured. Instead, only binary pairs forming electroneutral solutions can be measured. This problem leads to a redundancy in the evaluation of species standard state properties. The redundancy issue is resolved by setting the standard state chemical potential enthalpy, entropy, and volume for the hydrogen ion, H+, to zero, for every temperature and pressure. After this convention is applied, all other standard state properties of ionic species contain meaningfull information.
Ionic Strength
Most of the parameterizations within the model use the ionic strength as a key variable. The ionic strength, 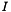 is defined as follows
is defined as follows
![\[ I = \frac{1}{2} \sum_k{m_k z_k^2} \]](form_35.png)
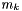 is the molality of the kth species.
is the molality of the kth species. 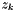 is the charge of the kth species. Note, the ionic strength is a defined units quantity. The molality has defined units of gmol kg-1, and therefore the ionic strength has units of sqrt( gmol kg-1).
is the charge of the kth species. Note, the ionic strength is a defined units quantity. The molality has defined units of gmol kg-1, and therefore the ionic strength has units of sqrt( gmol kg-1).
In some instances, from some authors, a different formulation is used for the ionic strength in the equations below. The different formulation is due to the possibility of the existence of weak acids and how association wrt to the weak acid equilibrium relation affects the calculation of the activity coefficients via the assumed value of the ionic strength.
If we are to assume that the association reaction doesn't have an effect on the ionic strength, then we will want to consider the associated weak acid as in effect being fully dissociated, when we calculate an effective value for the ionic strength. We will call this calculated value, the stoichiometric ionic strength, 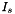 , putting a subscript s to denote it from the more straightforward calculation of
, putting a subscript s to denote it from the more straightforward calculation of 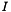 .
.
![\[ I_s = \frac{1}{2} \sum_k{m_k^s z_k^2} \]](form_40.png)
Here, 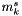 is the value of the molalities calculated assuming that all weak acid-base pairs are in their fully dissociated states. This calculation may be simplified by considering that the weakly associated acid may be made up of two charged species, k1 and k2, each with their own charges, obeying the following relationship:
is the value of the molalities calculated assuming that all weak acid-base pairs are in their fully dissociated states. This calculation may be simplified by considering that the weakly associated acid may be made up of two charged species, k1 and k2, each with their own charges, obeying the following relationship:
![\[ z_k = z_{k1} + z_{k2} \]](form_42.png)
Then, we may only need to specify one charge value, say, 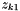 , the cation charge number, in order to get both numbers, since we have already specified
, the cation charge number, in order to get both numbers, since we have already specified 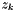 in the definition of original species. Then, the stoichiometric ionic strength may be calculated via the following formula.
in the definition of original species. Then, the stoichiometric ionic strength may be calculated via the following formula.
![\[ I_s = \frac{1}{2} \left(\sum_{k,ions}{m_k z_k^2}+ \sum_{k,weak_assoc}(m_k z_{k1}^2 + m_k z_{k2}^2) \right) \]](form_44.png)
The specification of which species are weakly associated acids is made in the input file via the stoichIsMods XML block, where the charge for k1 is also specified. An example is given below:
<stoichIsMods>
NaCl(aq):-1.0
</stoichIsMods>
Because we need the concept of a weakly associated acid in order to calculated 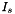 we need to catalog all species in the phase. This is done using the following categories:
we need to catalog all species in the phase. This is done using the following categories:
- cEST_solvent : Solvent species (neutral)
- cEST_chargedSpecies Charged species (charged)
- cEST_weakAcidAssociated Species which can break apart into charged species. It may or may not be charged. These may or may not be be included in the species solution vector.
- cEST_strongAcidAssociated Species which always breaksapart into charged species. It may or may not be charged. Normally, these aren't included in the speciation vector.
- cEST_polarNeutral Polar neutral species
- cEST_nonpolarNeutral Non poloar neutral species
Polar and non-polar neutral species are differentiated, because some additions to the activity coefficient expressions distinguish between these two types of solutes. This is the so-called salt-out effect.
The type of species is specified in the electrolyteSpeciesType XML block. Note, this is not considered a part of the specification of the standard state for the species, at this time. Therefore, this information is put under the activityCoefficient XML block. An example is given below
<electrolyteSpeciesType>
H2L(L):solvent
H+:chargedSpecies
NaOH(aq):weakAcidAssociated
NaCl(aq):strongAcidAssociated
NH3(aq):polarNeutral
O2(aq):nonpolarNeutral
</electrolyteSpeciesType>
Much of the species electrolyte type information is infered from other information in the input file. For example, as species which is charged is given the "chargedSpecies" default category. A neutral solute species is put into the "nonpolarNeutral" category by default.
Specification of the Excess Gibbs Free Energy
Pitzer's formulation may best be represented as a specification of the excess gibbs free energy, 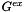 , defined as the deviation of the total gibbs free energy from that of an ideal molal solution.
, defined as the deviation of the total gibbs free energy from that of an ideal molal solution.
![\[ G = G^{id} + G^{ex} \]](form_113.png)
The ideal molal solution contribution, not equal to an ideal solution contribution and in fact containing a singularity at the zero solvent mole fraction limit, is given below.
![\[ G^{id} = n_o \mu^o_o + \sum_{k\ne o} n_k \mu_k^{\triangle} + \tilde{M}_o n_o ( RT (\sum{m_i(\ln(m_i)-1)})) \]](form_114.png)
From the excess Gibbs free energy formulation, the activity coefficient expression and the osmotic coefficient expression for the solvent may be defined, by taking the appropriate derivatives. Using this approach garranties that the entire system will obey the Gibbs-Duhem relations.
Pitzer employs the following general expression for the excess Gibbs free energy
![\[ \begin{array}{cclc} \frac{G^{ex}}{\tilde{M}_o n_o RT} &= & \left( \frac{4A_{Debye}I}{3b} \right) \ln(1 + b \sqrt{I}) + 2 \sum_c \sum_a m_c m_a B_{ca} + \sum_c \sum_a m_c m_a Z C_{ca} \\&& + \sum_{c < c'} \sum m_c m_{c'} \left[ 2 \Phi_{c{c'}} + \sum_a m_a \Psi_{c{c'}a} \right] + \sum_{a < a'} \sum m_a m_{a'} \left[ 2 \Phi_{a{a'}} + \sum_c m_c \Psi_{a{a'}c} \right] \\&& + 2 \sum_n \sum_c m_n m_c \lambda_{nc} + 2 \sum_n \sum_a m_n m_a \lambda_{na} + 2 \sum_{n < n'} \sum m_n m_{n'} \lambda_{n{n'}} + \sum_n m^2_n \lambda_{nn} \end{array} \]](form_115.png)
a is a subscribt over all anions, c is a subscript extending over all cations, and i is a subscrit that extends over all anions and cations. n is a subscript that extends only over neutral solute molecules. The second line contains cross terms where cations affect cations and/or cation/anion pairs, and anions affect anions or cation/anion pairs. Note part of the coefficients, 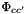 and
and  stem from the theory of unsymmetrical mixing of electrolytes with different charges. This theory depends on the total ionic stregnth of the solution, and therefore,
stem from the theory of unsymmetrical mixing of electrolytes with different charges. This theory depends on the total ionic stregnth of the solution, and therefore, 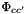 and
and  will depend on I, the ionic strength.
will depend on I, the ionic strength. 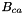 is a strong function of the total ionic strength, I, of the electrolyte. The rest of the coefficients are assumed to be independent of the molalities or ionic strengths. However, all coefficients are potentially functions of the temperature and pressure of the solution.
is a strong function of the total ionic strength, I, of the electrolyte. The rest of the coefficients are assumed to be independent of the molalities or ionic strengths. However, all coefficients are potentially functions of the temperature and pressure of the solution.
A is the Debye-Huckel constant. It's specification is described in its own section below.
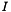 is the ionic strength of the solution, and is given by:
is the ionic strength of the solution, and is given by:
![\[ I = \frac{1}{2} \sum_k{m_k z_k^2} \]](form_35.png)
In contrast to several other Debye-Huckel implementations (see DebyeHuckel), the parameter 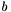 in the above equation is a constant that doesn not vary with respect to ion idenity. This is an important simplification as it avoids troubles with satisfaction of the Gibbs-Duhem analysis.
in the above equation is a constant that doesn not vary with respect to ion idenity. This is an important simplification as it avoids troubles with satisfaction of the Gibbs-Duhem analysis.
The function 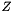 is given by
is given by
![\[ Z = \sum_i m_i \left| z_i \right| \]](form_121.png)
The value of 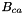 is given by the following function
is given by the following function
![\[ B_{ca} = \beta^{(0)}_{ca} + \beta^{(1)}_{ca} g(\alpha^{(1)}_{ca} \sqrt{I}) + \beta^{(2)}_{ca} g(\alpha^{(2)}_{ca} \sqrt{I}) \]](form_122.png)
where
![\[ g(x) = 2 \frac{(1 - (1 + x)\exp[-x])}{x^2} \]](form_123.png)
The formulation for 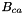 combined with the formulation of the Debye-Huckel term in the eqn. for the excess Gibbs free energy stems essentially from an empirical fit to the ionic strength dependent data based over a wide sampling of binary electroyte systems.
combined with the formulation of the Debye-Huckel term in the eqn. for the excess Gibbs free energy stems essentially from an empirical fit to the ionic strength dependent data based over a wide sampling of binary electroyte systems. 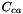 ,
, 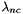 ,
, 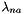 ,
, 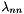 ,
, 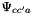 ,
, 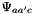 are experimentally derived coefficients that may have pressure and/or temperature dependencies. The
are experimentally derived coefficients that may have pressure and/or temperature dependencies. The 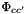 and
and  formulations are slightly more complicated.
formulations are slightly more complicated. 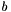 is a univeral constant defined to be equal to
is a univeral constant defined to be equal to 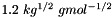 . The exponential coefficient
. The exponential coefficient 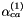 is usually fixed at
is usually fixed at 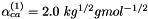 except for 2-2 electrolytes, while other parameters were fit to experimental data. For 2-2 electrolytes,
except for 2-2 electrolytes, while other parameters were fit to experimental data. For 2-2 electrolytes, 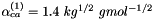 is used in combination with either
is used in combination with either 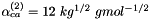 or
or 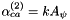 , where k is a constant. For electrolytes other than 2-2 electrolytes the
, where k is a constant. For electrolytes other than 2-2 electrolytes the 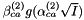 term is not used in the fitting procedure; it is only used for divalent metal solfates and other high-valence electrolytes which exhibit significant association at low ionic strengths.
term is not used in the fitting procedure; it is only used for divalent metal solfates and other high-valence electrolytes which exhibit significant association at low ionic strengths.
The 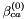 ,
, 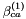 ,
, 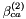 , and
, and 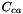 binary coefficients are referred to as ion-interaction or Pitzer parameters. These Pitzer parameters may vary with temperature and pressure but they do not depend on the ionic strength. Their values and temperature derivatives of their values have been tabulated for a range of electrolytes
binary coefficients are referred to as ion-interaction or Pitzer parameters. These Pitzer parameters may vary with temperature and pressure but they do not depend on the ionic strength. Their values and temperature derivatives of their values have been tabulated for a range of electrolytes
The 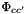 and
and  contributions, which capture cation-cation and anion-anion interactions, also have an ionic strength dependence.
contributions, which capture cation-cation and anion-anion interactions, also have an ionic strength dependence.
Ternary contributions 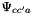 and
and 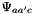 have been measured also for some systems. The success of the Pitzer method lies in its ability to model nonlinear activity coefficients of complex multicomponent systems with just binary and minor ternary contributions, which can be independently measured in binary or ternary subsystems.
have been measured also for some systems. The success of the Pitzer method lies in its ability to model nonlinear activity coefficients of complex multicomponent systems with just binary and minor ternary contributions, which can be independently measured in binary or ternary subsystems.
Multicomponent Activity Coefficients for Solutes
The formulas for activity coefficients of solutes may be obtained by taking the following derivative of the excess Gibbs Free Energy formulation described above:
![\[ \ln(\gamma_k^\triangle) = \frac{d\left( \frac{G^{ex}}{M_o n_o RT} \right)}{d(m_k)}\Bigg|_{n_i} \]](form_141.png)
In the formulas below the following conventions are used. The subscript M refers to a particular cation. The subscript X refers to a particular anion, whose activity is being currently evaluated. the subscript a refers to a summation over all anions in the solution, while the subscript c refers to a summation over all cations in the solutions.
The activity coefficient for a particular cation M is given by
![\[ \ln(\gamma_M^\triangle) = -z_M^2(F) + \sum_a m_a \left( 2 B_{Ma} + Z C_{Ma} \right) + z_M \left( \sum_a \sum_c m_a m_c C_{ca} \right) + \sum_c m_c \left[ 2 \Phi_{Mc} + \sum_a m_a \Psi_{Mca} \right] + \sum_{a < a'} \sum m_a m_{a'} \Psi_{Ma{a'}} + 2 \sum_n m_n \lambda_{nM} \]](form_142.png)
The activity coefficient for a particular anion X is given by
![\[ \ln(\gamma_X^\triangle) = -z_X^2(F) + \sum_a m_c \left( 2 B_{cX} + Z C_{cX} \right) + \left|z_X \right| \left( \sum_a \sum_c m_a m_c C_{ca} \right) + \sum_a m_a \left[ 2 \Phi_{Xa} + \sum_c m_c \Psi_{cXa} \right] + \sum_{c < c'} \sum m_c m_{c'} \Psi_{c{c'}X} + 2 \sum_n m_n \lambda_{nM} \]](form_143.png)
where the function 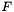 is given by
is given by
![\[ F = - A_{\phi} \left[ \frac{\sqrt{I}}{1 + b \sqrt{I}} + \frac{2}{b} \ln{\left(1 + b\sqrt{I}\right)} \right] + \sum_a \sum_c m_a m_c B'_{ca} + \sum_{c < c'} \sum m_c m_{c'} \Phi'_{c{c'}} + \sum_{a < a'} \sum m_a m_{a'} \Phi'_{a{a'}} \]](form_145.png)
We have employed the definition of 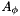 , also used by Pitzer which is equal to
, also used by Pitzer which is equal to
![\[ A_{\phi} = \frac{A_{Debye}}{3} \]](form_147.png)
In the above formulas, 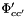 and
and 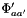 are the ionic strength derivatives of
are the ionic strength derivatives of 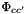 and
and  , respectively.
, respectively.
The function 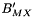 is defined as:
is defined as:
![\[ B'_{MX} = \left( \frac{\beta^{(1)}_{MX} h(\alpha^{(1)}_{MX} \sqrt{I})}{I} \right) \left( \frac{\beta^{(2)}_{MX} h(\alpha^{(2)}_{MX} \sqrt{I})}{I} \right) \]](form_151.png)
where 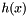 is defined as
is defined as
![\[ h(x) = g'(x) \frac{x}{2} = \frac{2\left(1 - \left(1 + x + \frac{x^2}{2} \right)\exp(-x) \right)}{x^2} \]](form_153.png)
The activity coefficient for neutral species N is given by
![\[ \ln(\gamma_N^\triangle) = 2 \left( \sum_i m_i \lambda_{iN}\right) \]](form_154.png)
Activity of the Water Solvent
The activity for the solvent water,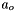 , is not independent and must be determined either from the Gibbs-Duhem relation or from taking the appropriate derivative of the same excess Gibbs free energy function as was used to formulate the solvent activity coefficients. Pitzer's description follows the later approach to derive a formula for the osmotic coefficient,
, is not independent and must be determined either from the Gibbs-Duhem relation or from taking the appropriate derivative of the same excess Gibbs free energy function as was used to formulate the solvent activity coefficients. Pitzer's description follows the later approach to derive a formula for the osmotic coefficient, 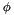 .
.
![\[ \phi - 1 = - \left( \frac{d\left(\frac{G^{ex}}{RT} \right)}{d(\tilde{M}_o n_o)} \right) \frac{1}{\sum_{i \ne 0} m_i} \]](form_156.png)
The osmotic coefficient may be related to the water activity by the following relation:
![\[ \phi = - \frac{1}{\tilde{M}_o \sum_{i \neq o} m_i} \ln(a_o) = - \frac{n_o}{\sum_{i \neq o}n_i} \ln(a_o) \]](form_157.png)
The result is the following
![\[ \begin{array}{ccclc} \phi - 1 &= & \frac{2}{\sum_{i \ne 0} m_i} \bigg[ & - A_{\phi} \frac{I^{3/2}}{1 + b \sqrt{I}} + \sum_c \sum_a m_c m_a \left( B^{\phi}_{ca} + Z C_{ca}\right) \\&&& + \sum_{c < c'} \sum m_c m_{c'} \left[ \Phi^{\phi}_{c{c'}} + \sum_a m_a \Psi_{c{c'}a} \right] + \sum_{a < a'} \sum m_a m_{a'} \left[ \Phi^{\phi}_{a{a'}} + \sum_c m_c \Psi_{a{a'}c} \right] \\&&& + \sum_n \sum_c m_n m_c \lambda_{nc} + \sum_n \sum_a m_n m_a \lambda_{na} + \sum_{n < n'} \sum m_n m_{n'} \lambda_{n{n'}} + \frac{1}{2} \left( \sum_n m^2_n \lambda_{nn}\right) \bigg] \end{array} \]](form_158.png)
It can be shown that the expression
![\[ B^{\phi}_{ca} = \beta^{(0)}_{ca} + \beta^{(1)}_{ca} \exp{(- \alpha^{(1)}_{ca} \sqrt{I})} + \beta^{(2)}_{ca} \exp{(- \alpha^{(2)}_{ca} \sqrt{I} )} \]](form_159.png)
is consistent with the expression 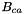 in the
in the 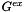 expression after carrying out the derivative wrt
expression after carrying out the derivative wrt 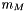 .
.
Also taking into account that 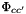 and
and 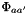 has an ionic strength dependence.
has an ionic strength dependence.
![\[ \Phi^{\phi}_{c{c'}} = {\Phi}_{c{c'}} + I \frac{d{\Phi}_{c{c'}}}{dI} \]](form_164.png)
![\[ \Phi^{\phi}_{a{a'}} = \Phi_{a{a'}} + I \frac{d\Phi_{a{a'}}}{dI} \]](form_165.png)
Temperature and Pressure Dependence of the Pitzer Parameters
In general most of the coefficients introduced in the previous section may have a temperature and pressure dependence. The temperature and pressure dependence of these coefficients strongly influence the value of the excess Enthalpy and excess Volumes of Pitzer solutions. Therefore, these are readily measurable quantities. HMWSoln provides several different methods for putting these dependencies into the coefficients. HMWSoln has an implementation described by Silverter and Pitzer (1977), which was used to fit experimental data for NaCl over an extensive range, below the critical temperature of water. They found a temperature funcdtional form for fitting the 3 following coefficients that describe the Pitzer parameterization for a single salt to be adequate to describe how the excess gibbs free energy values for the binary salt changes with respect to temperature. The following functional form was used to fit the temperature dependence of the Pitzer Coefficients for each cation - anion pair, M X.
![\[ \beta^{(0)}_{MX} = q^{b0}_0 + q^{b0}_1 \left( T - T_r \right) + q^{b0}_2 \left( T^2 - T_r^2 \right) + q^{b0}_3 \left( \frac{1}{T} - \frac{1}{T_r}\right) + q^{b0}_4 \ln \left( \frac{T}{T_r} \right) \]](form_166.png)
![\[ \beta^{(1)}_{MX} = q^{b1}_0 + q^{b1}_1 \left( T - T_r \right) + q^{b1}_{2} \left( T^2 - T_r^2 \right) \]](form_167.png)
![\[ C^{\phi}_{MX} = q^{Cphi}_0 + q^{Cphi}_1 \left( T - T_r \right) + q^{Cphi}_2 \left( T^2 - T_r^2 \right) + q^{Cphi}_3 \left( \frac{1}{T} - \frac{1}{T_r}\right) + q^{Cphi}_4 \ln \left( \frac{T}{T_r} \right) \]](form_168.png)
where
![\[ C^{\phi}_{MX} = 2 {\left| z_M z_X \right|}^{1/2} C_{MX} \]](form_169.png)
In later papers, Pitzer has added additional temperature dependencies to all of the other remaining second and third order virial coefficients. Some of these dependencies are justified and motivated by theory. Therefore, a formalism wherein all of the coefficients in the base theory have temperature dependencies associated with them has been implemented within the HMWSoln object. Much of the formalism, however, has been unexercised.
In the HMWSoln object, the temperature dependence of the Pitzer parameters are specified in the following way.
- PIZTER_TEMP_CONSTANT - string name "CONSTANT"
- Assumes that all coefficients are independent of temperature and pressure
- PIZTER_TEMP_COMPLEX1 - string name "COMPLEX" or "COMPLEX1"
- Uses the full temperature dependence for the
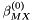 (5 coeffs), the
(5 coeffs), the 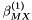 (3 coeffs), and
(3 coeffs), and 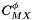 (5 coeffs) parameters described above.
(5 coeffs) parameters described above.
- Uses the full temperature dependence for the
- PITZER_TEMP_LINEAR - string name "LINEAR"
- Uses just the temperature dependence for the
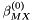 , the
, the 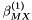 , and
, and 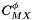 coefficients described above. There are 2 coefficients for each term.
coefficients described above. There are 2 coefficients for each term.
- Uses just the temperature dependence for the
The temperature dependence is specified in an attributes field in the activityCoefficients XML block, called TempModel . Permissible values for that attribute are CONSTANT, COMPLEX1, and LINEAR.
The specification of the binary interaction between a cation and an anion is given by the coefficients, 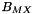 and
and 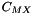 The specification of
The specification of 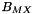 is a function of
is a function of 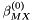 ,
, 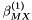 ,
, 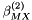 ,
, 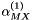 , and
, and 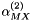 .
. 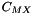 is calculated from
is calculated from 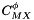 from the formula above. All of the underlying coeficients are specified in the XML element block
from the formula above. All of the underlying coeficients are specified in the XML element block binarySaltParameters , which has the attribute cation and anion to identify the interaction. XML elements named beta0, beta1, beta2, Cphi, Alpha1, Alpha2 within each binarySaltParameters block specify the parameters. Within each of these blocks multiple parameters describing temperature or pressure dependence are serially listed in the order that they appear in the equation in this document. An example of the beta0 block that fits the COMPLEX1 temperature dependence given above is
<binarySaltParameters cation="Na+" anion="OH-"> <beta0> q0, q1, q2, q3, q4 </beta0> </binarySaltParameters>
The parameters for 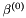 fit the following equation:
fit the following equation:
![\[ \beta^{(0)} = q_0^{{\beta}0} + q_1^{{\beta}0} \left( T - T_r \right) + q_2^{{\beta}0} \left( T^2 - T_r^2 \right) + q_3^{{\beta}0} \left( \frac{1}{T} - \frac{1}{T_r} \right) + q_4^{{\beta}0} \ln \left( \frac{T}{T_r} \right) \]](form_180.png)
This same COMPLEX1 temperature dependence given above is used for the following parameters: 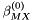 ,
, 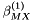 ,
, 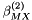 ,
, 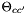 ,
, 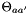 ,
, 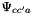 and
and 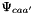 .
.
Like-Charged Binary Ion Parameters and the Mixing Parameters
The previous section contained the functions, 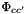 ,
,  and their derivatives wrt the ionic strength,
and their derivatives wrt the ionic strength, 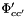 and
and 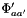 . Part of these terms come from theory.
. Part of these terms come from theory.
Since like charged ions repel each other and are generally not near each other, the virial coefficients for same-charged ions are small. However, Pitzer doesn't ignore these in his formulation. Relatively larger and longer range terms between like-charged ions exist however, which appear only for unsymmetrical mixing of same-sign charged ions with different charges. 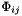 , where
, where 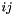 is either
is either 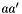 or
or 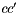 is given by
is given by
![\[ {\Phi}_{ij} = \Theta_{ij} + \,^E \Theta_{ij}(I) \]](form_191.png)
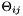 is the small virial coefficient expansion term. Dependent in general on temperature and pressure, it's ionic strength dependence is ignored in Pitzer's approach.
is the small virial coefficient expansion term. Dependent in general on temperature and pressure, it's ionic strength dependence is ignored in Pitzer's approach. 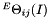 accounts for the electrostatic unsymmetrical mixing effects and is dependent only on the charges of the ions i, j, the total ionic strength and on the dielectric constant and density of the solvent. This seems to be a relatively well-documented part of the theory. They theory below comes from Pitzer summation (Pitzer) in the appendix. It's also mentioned in Bethke's book (Bethke), and the equations are summarized in Harvie & Weare (1980). Within the code,
accounts for the electrostatic unsymmetrical mixing effects and is dependent only on the charges of the ions i, j, the total ionic strength and on the dielectric constant and density of the solvent. This seems to be a relatively well-documented part of the theory. They theory below comes from Pitzer summation (Pitzer) in the appendix. It's also mentioned in Bethke's book (Bethke), and the equations are summarized in Harvie & Weare (1980). Within the code, 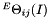 is evaluated according to the algorithm described in Appendix B [Pitzer] as
is evaluated according to the algorithm described in Appendix B [Pitzer] as
![\[ \,^E\Theta_{ij}(I) = \left( \frac{z_i z_j}{4I} \right) \left( J(x_{ij}) - \frac{1}{2} J(x_{ii}) - \frac{1}{2} J(x_{jj}) \right) \]](form_194.png)
where 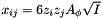 and
and
![\[ J(x) = \frac{1}{x} \int_0^{\infty}{\left( 1 + q + \frac{1}{2} q^2 - e^q \right) y^2 dy} \]](form_196.png)
and 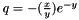 .
. 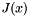 is evaluated by numerical integration.
is evaluated by numerical integration.
The 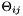 term is a constant that is specified by the XML element
term is a constant that is specified by the XML element thetaCation and thetaAnion , which has the attribute cation1 , cation2 and anion1 , anion2 respectively to identify the interaction. No temperature or pressure dependence of this parameter is currently allowed. An example of the block is presented below.
<thetaCation cation1="Na+" cation2="H+"> <Theta> 0.036 </Theta> </thetaCation>
Ternary Pitzer Parameters
The 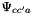 and
and 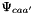 terms represent ternary interactions between two cations and an anion and two anions and a cation, respectively. In Pitzer's implementation these terms are usually small in absolute size. Currently these parameters do not have any dependence on temperature, pressure, or ionic strength.
terms represent ternary interactions between two cations and an anion and two anions and a cation, respectively. In Pitzer's implementation these terms are usually small in absolute size. Currently these parameters do not have any dependence on temperature, pressure, or ionic strength.
Their values are input using the XML element psiCommonCation and psiCommonAnion . The species id's are specified in attribute fields in the XML element. The fields cation, anion1, and anion2 are used for psiCommonCation. The fields anion, cation1 and cation2 are used for psiCommonAnion. An example block is given below. The Theta field below is a duplicate of the thetaAnion field mentioned above. The two fields are input into the same block for convenience, and because their data are highly correlated, in practice. It is an error for the two blocks to specify different information about thetaAnion (or thetaCation) in different blocks. It's ok to specify duplicate but consistent information in multiple blocks.
<psiCommonCation cation="Na+" anion1="Cl-" anion2="OH-"> <Theta> -0.05 </Theta> <Psi> -0.006 </Psi> </psiCommonCation>
Treatment of Neutral Species
Binary virial-coefficient-like interactions between two neutral species may be specified in the 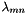 terms that appear in the formulas above. Currently these interactions are independent of temperature, pressure, and ionic strength. Also, currently, the neutrality of the species are not checked. Therefore, this interaction may involve charged species in the solution as well. The identity of the species is specified by the
terms that appear in the formulas above. Currently these interactions are independent of temperature, pressure, and ionic strength. Also, currently, the neutrality of the species are not checked. Therefore, this interaction may involve charged species in the solution as well. The identity of the species is specified by the species1 and species2 attributes to the XML lambdaNeutral node. These terms are symmetrical; species1 and species2 may be reversed and the term will be the same. An example is given below.
<lambdaNeutral species1="CO2" species2="CH4"> <lambda> 0.05 </lambda> </lambdaNeutral>
Example of the Specification of Parameters for the Activity Coefficients
An example is given below.
An example activityCoefficients XML block for this formulation is supplied below
<activityCoefficients model="Pitzer" TempModel="complex1">
<!-- Pitzer Coefficients
These coefficients are from Pitzer's main
paper, in his book.
-->
<A_Debye model="water" />
<ionicRadius default="3.042843" units="Angstroms">
</ionicRadius>
<binarySaltParameters cation="Na+" anion="Cl-">
<beta0> 0.0765, 0.008946, -3.3158E-6,
-777.03, -4.4706
</beta0>
<beta1> 0.2664, 6.1608E-5, 1.0715E-6, 0.0, 0.0 </beta1>
<beta2> 0.0, 0.0, 0.0, 0.0, 0.0 </beta2>
<Cphi> 0.00127, -4.655E-5, 0.0,
33.317, 0.09421
</Cphi>
<Alpha1> 2.0 </Alpha1>
</binarySaltParameters>
<binarySaltParameters cation="H+" anion="Cl-">
<beta0> 0.1775, 0.0, 0.0, 0.0, 0.0 </beta0>
<beta1> 0.2945, 0.0, 0.0, 0.0, 0.0 </beta1>
<beta2> 0.0, 0.0, 0.0, 0.0, 0.0 </beta2>
<Cphi> 0.0008, 0.0, 0.0, 0.0, 0.0 </Cphi>
<Alpha1> 2.0 </Alpha1>
</binarySaltParameters>
<binarySaltParameters cation="Na+" anion="OH-">
<beta0> 0.0864, 0.0, 0.0, 0.0, 0.0 </beta0>
<beta1> 0.253, 0.0, 0.0 0.0, 0.0 </beta1>
<beta2> 0.0 0.0, 0.0, 0.0, 0.0 </beta2>
<Cphi> 0.0044, 0.0, 0.0, 0.0, 0.0 </Cphi>
<Alpha1> 2.0 </Alpha1>
</binarySaltParameters>
<thetaAnion anion1="Cl-" anion2="OH-">
<Theta> -0.05, 0.0, 0.0, 0.0, 0.0 </Theta>
</thetaAnion>
<psiCommonCation cation="Na+" anion1="Cl-" anion2="OH-">
<Theta> -0.05, 0.0, 0.0, 0.0, 0.0 </Theta>
<Psi> -0.006 </Psi>
</psiCommonCation>
<thetaCation cation1="Na+" cation2="H+">
<Theta> 0.036, 0.0, 0.0, 0.0, 0.0 </Theta>
</thetaCation>
<psiCommonAnion anion="Cl-" cation1="Na+" cation2="H+">
<Theta> 0.036, 0.0, 0.0, 0.0, 0.0 </Theta>
<Psi> -0.004 </Psi>
</psiCommonAnion>
</activityCoefficients>
Specification of the Debye-Huckel Constant
In the equations above, the formula for 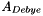 is needed. The HMWSoln object uses two methods for specifying these quantities. The default method is to assume that
is needed. The HMWSoln object uses two methods for specifying these quantities. The default method is to assume that 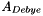 is a constant, given in the initialization process, and storred in the member double, m_A_Debye. Optionally, a full water treatment may be employed that makes
is a constant, given in the initialization process, and storred in the member double, m_A_Debye. Optionally, a full water treatment may be employed that makes 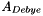 a full function of T and P and creates nontrivial entries for the excess heat capacity, enthalpy, and excess volumes of solution.
a full function of T and P and creates nontrivial entries for the excess heat capacity, enthalpy, and excess volumes of solution.
![\[ A_{Debye} = \frac{F e B_{Debye}}{8 \pi \epsilon R T} {\left( C_o \tilde{M}_o \right)}^{1/2} \]](form_64.png)
where
![\[ B_{Debye} = \frac{F} {{(\frac{\epsilon R T}{2})}^{1/2}} \]](form_65.png)
Therefore:
![\[ A_{Debye} = \frac{1}{8 \pi} {\left(\frac{2 N_a \rho_o}{1000}\right)}^{1/2} {\left(\frac{N_a e^2}{\epsilon R T }\right)}^{3/2} \]](form_66.png)
Units = sqrt(kg/gmol)
where
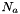 is Avrogadro's number
is Avrogadro's number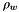 is the density of water
is the density of water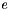 is the electronic charge
is the electronic charge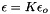 is the permitivity of water where
is the permitivity of water where 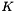 is the dielectric constant of water, and
is the dielectric constant of water, and 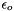 is the permitivity of free space.
is the permitivity of free space.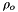 is the density of the solvent in its standard state.
is the density of the solvent in its standard state.
Nominal value at 298 K and 1 atm = 1.172576 (kg/gmol)1/2 based on:
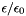 = 78.54 (water at 25C)
= 78.54 (water at 25C)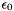 = 8.854187817E-12 C2 N-1 m-2
= 8.854187817E-12 C2 N-1 m-2- e = 1.60217653E-19 C
- F = 9.6485309E7 C kmol-1
- R = 8.314472E3 kg m2 s-2 kmol-1 K-1
- T = 298.15 K
- B_Debye = 3.28640E9 (kg/gmol)1/2 m-1
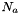 = 6.0221415E26 kmol-1
= 6.0221415E26 kmol-1
An example of a fixed value implementation is given below.
<activityCoefficients model="Pitzer"> <!-- A_Debye units = sqrt(kg/gmol) --> <A_Debye> 1.172576 </A_Debye> <!-- object description continues --> </activityCoefficients>
An example of a variable value implementation within the HMWSoln object is given below. The model attribute, "water", triggers the full implementation.
<activityCoefficients model="Pitzer"> <!-- A_Debye units = sqrt(kg/gmol) --> <A_Debye model="water" /> <!-- object description continues --> </activityCoefficients>
Temperature and Pressure Dependence of the Activity Coefficients
Temperature dependence of the activity coefficients leads to nonzero terms for the excess enthalpy and entropy of solution. This means that the partial molar enthalpies, entropies, and heat capacities are all non-trivial to compute. The following formulas are used.
The partial molar enthalpy, 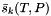 :
:
![\[ \bar h_k(T,P) = h^{\triangle}_k(T,P) - R T^2 \frac{d \ln(\gamma_k^\triangle)}{dT} \]](form_103.png)
The solvent partial molar enthalpy is equal to
![\[ \bar h_o(T,P) = h^{o}_o(T,P) - R T^2 \frac{d \ln(a_o)}{dT} = h^{o}_o(T,P) + R T^2 (\sum_{k \neq o} m_k) \tilde{M_o} (\frac{d \phi}{dT}) \]](form_201.png)
The partial molar entropy, 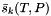 :
:
![\[ \bar s_k(T,P) = s^{\triangle}_k(T,P) - R \ln( \gamma^{\triangle}_k \frac{m_k}{m^{\triangle}})) - R T \frac{d \ln(\gamma^{\triangle}_k) }{dT} \]](form_202.png)
![\[ \bar s_o(T,P) = s^o_o(T,P) - R \ln(a_o) - R T \frac{d \ln(a_o)}{dT} \]](form_203.png)
The partial molar heat capacity, 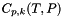 :
:
![\[ \bar C_{p,k}(T,P) = C^{\triangle}_{p,k}(T,P) - 2 R T \frac{d \ln( \gamma^{\triangle}_k)}{dT} - R T^2 \frac{d^2 \ln(\gamma^{\triangle}_k) }{{dT}^2} \]](form_205.png)
![\[ \bar C_{p,o}(T,P) = C^o_{p,o}(T,P) - 2 R T \frac{d \ln(a_o)}{dT} - R T^2 \frac{d^2 \ln(a_o)}{{dT}^2} \]](form_206.png)
The pressure dependence of the activity coefficients leads to non-zero terms for the excess Volume of the solution. Therefore, the partial molar volumes are functions of the pressure derivatives of the activity coefficients.
![\[ \bar V_k(T,P) = V^{\triangle}_k(T,P) + R T \frac{d \ln(\gamma^{\triangle}_k) }{dP} \]](form_207.png)
![\[ \bar V_o(T,P) = V^o_o(T,P) + R T \frac{d \ln(a_o)}{dP} \]](form_208.png)
The majority of work for these functions take place in the internal routines that calculate the first and second derivatives of the log of the activity coefficients wrt temperature, s_update_dlnMolalityActCoeff_dT(), s_update_d2lnMolalityActCoeff_dT2(), and the first derivative of the log activity coefficients wrt pressure, s_update_dlnMolalityActCoeff_dP().
Application within Kinetics Managers
For the time being, we have set the standard concentration for all solute species in this phase equal to the default concentration of the solvent at the system temperature and pressure multiplied by Mnaught (kg solvent / gmol solvent). The solvent standard concentration is just equal to its standard state concentration.
This means that the kinetics operator essentially works on an generalized concentration basis (kmol / m3), with units for the kinetic rate constant specified as if all reactants (solvent or solute) are on a concentration basis (kmol /m3). The concentration will be modified by the activity coefficients.
For example, a bulk-phase binary reaction between liquid solute species j and k, producing a new liquid solute species l would have the following equation for its rate of progress variable, 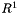 , which has units of kmol m-3 s-1.
, which has units of kmol m-3 s-1.
![\[ R^1 = k^1 C_j^a C_k^a = k^1 (C^o_o \tilde{M}_o a_j) (C^o_o \tilde{M}_o a_k) \]](form_209.png)
where
![\[ C_j^a = C^o_o \tilde{M}_o a_j \quad and \quad C_k^a = C^o_o \tilde{M}_o a_k \]](form_210.png)
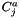 is the activity concentration of species j, and
is the activity concentration of species j, and 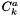 is the activity concentration of species k.
is the activity concentration of species k. 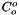 is the concentration of water at 298 K and 1 atm.
is the concentration of water at 298 K and 1 atm. 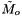 has units of kg solvent per gmol solvent and is equal to
has units of kg solvent per gmol solvent and is equal to
![\[ \tilde{M}_o = \frac{M_o}{1000} \]](form_213.png)
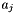 is the activity of species j at the current temperature and pressure and concentration of the liquid phase is given by the molality based activity coefficient multiplied by the molality of the jth species.
is the activity of species j at the current temperature and pressure and concentration of the liquid phase is given by the molality based activity coefficient multiplied by the molality of the jth species.
![\[ a_j = \gamma_j^\triangle m_j = \gamma_j^\triangle \frac{n_j}{\tilde{M}_o n_o} \]](form_214.png)
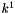 has units of m3 kmol-1 s-1.
has units of m3 kmol-1 s-1.
Therefore the generalized activity concentration of a solute species has the following form
![\[ C_j^a = C^o_o \frac{\gamma_j^\triangle n_j}{n_o} \]](form_215.png)
The generalized activity concentration of the solvent has the same units, but its a simpler form
![\[ C_o^a = C^o_o a_o \]](form_216.png)
The reverse rate constant can then be obtained from the law of microscopic reversibility and the equilibrium expression for the system.
![\[ \frac{a_j a_k}{ a_l} = K^{o,1} = \exp(\frac{\mu^o_l - \mu^o_j - \mu^o_k}{R T} ) \]](form_84.png)
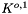 is the dimensionless form of the equilibrium constant.
is the dimensionless form of the equilibrium constant.
![\[ R^{-1} = k^{-1} C_l^a = k^{-1} (C_o \tilde{M}_o a_l) \]](form_217.png)
where
![\[ k^{-1} = k^1 K^{o,1} C_o \tilde{M}_o \]](form_218.png)
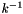 has units of s-1.
has units of s-1.
Note, this treatment may be modified in the future, as events dictate.
Instantiation of the Class
The constructor for this phase is now located in the default ThermoFactory for Cantera. The following code snipet may be used to initialize the phase using the default construction technique within Cantera.
ThermoPhase *HMW = newPhase("HMW_NaCl.xml", "NaCl_electrolyte");
A new HMWSoln object may be created by the following code snippets:
or
char iFile[80], file_ID[80]; strcpy(iFile, "HMW_NaCl.xml"); sprintf(file_ID,"%s#NaCl_electrolyte", iFile); XML_Node *xm = get_XML_NameID("phase", file_ID, 0); HMWSoln *dh = new HMWSoln(*xm);
or by the following call to importPhase():
char iFile[80], file_ID[80]; strcpy(iFile, "HMW_NaCl.xml"); sprintf(file_ID,"%s#NaCl_electrolyte", iFile); XML_Node *xm = get_XML_NameID("phase", file_ID, 0); HMWSoln dhphase; importPhase(*xm, &dhphase);
XML Example
The phase model name for this is called StoichSubstance. It must be supplied as the model attribute of the thermo XML element entry. Within the phase XML block, the density of the phase must be specified. An example of an XML file this phase is given below.
<phase id="NaCl_electrolyte" dim="3">
<speciesArray datasrc="#species_waterSolution">
H2O(L) Na+ Cl- H+ OH-
</speciesArray>
<state>
<temperature units="K"> 300 </temperature>
<pressure units="Pa">101325.0</pressure>
<soluteMolalities>
Na+:3.0
Cl-:3.0
H+:1.0499E-8
OH-:1.3765E-6
</soluteMolalities>
</state>
<!-- thermo model identifies the inherited class
from ThermoPhase that will handle the thermodynamics.
-->
<thermo model="HMW">
<standardConc model="solvent_volume" />
<activityCoefficients model="Pitzer" TempModel="complex1">
<!-- Pitzer Coefficients
These coefficients are from Pitzer's main
paper, in his book.
-->
<A_Debye model="water" />
<ionicRadius default="3.042843" units="Angstroms">
</ionicRadius>
<binarySaltParameters cation="Na+" anion="Cl-">
<beta0> 0.0765, 0.008946, -3.3158E-6,
-777.03, -4.4706
</beta0>
<beta1> 0.2664, 6.1608E-5, 1.0715E-6 </beta1>
<beta2> 0.0 </beta2>
<Cphi> 0.00127, -4.655E-5, 0.0,
33.317, 0.09421
</Cphi>
<Alpha1> 2.0 </Alpha1>
</binarySaltParameters>
<binarySaltParameters cation="H+" anion="Cl-">
<beta0> 0.1775, 0.0, 0.0, 0.0, 0.0</beta0>
<beta1> 0.2945, 0.0, 0.0 </beta1>
<beta2> 0.0 </beta2>
<Cphi> 0.0008, 0.0, 0.0, 0.0, 0.0 </Cphi>
<Alpha1> 2.0 </Alpha1>
</binarySaltParameters>
<binarySaltParameters cation="Na+" anion="OH-">
<beta0> 0.0864, 0.0, 0.0, 0.0, 0.0 </beta0>
<beta1> 0.253, 0.0, 0.0 </beta1>
<beta2> 0.0 </beta2>
<Cphi> 0.0044, 0.0, 0.0, 0.0, 0.0 </Cphi>
<Alpha1> 2.0 </Alpha1>
</binarySaltParameters>
<thetaAnion anion1="Cl-" anion2="OH-">
<Theta> -0.05 </Theta>
</thetaAnion>
<psiCommonCation cation="Na+" anion1="Cl-" anion2="OH-">
<Theta> -0.05 </Theta>
<Psi> -0.006 </Psi>
</psiCommonCation>
<thetaCation cation1="Na+" cation2="H+">
<Theta> 0.036 </Theta>
</thetaCation>
<psiCommonAnion anion="Cl-" cation1="Na+" cation2="H+">
<Theta> 0.036 </Theta>
<Psi> -0.004 </Psi>
</psiCommonAnion>
</activityCoefficients>
<solvent> H2O(L) </solvent>
</thermo>
<elementArray datasrc="elements.xml"> O H Na Cl </elementArray>
<kinetics model="none" >
</kinetics>
</phase>
Definition at line 1248 of file HMWSoln.h.
Constructor & Destructor Documentation
| HMWSoln | ( | ) |
Default Constructor.
Definition at line 34 of file HMWSoln.cpp.
References PITZERFORM_BASE.
Referenced by HMWSoln::duplMyselfAsThermoPhase().
| HMWSoln | ( | std::string | inputFile, | |
| std::string | id = "" | |||
| ) |
Construct and initialize an HMWSoln ThermoPhase object directly from an asci input file.
Working constructors
The two constructors below are the normal way the phase initializes itself. They are shells that call the routine initThermo(), with a reference to the XML database to get the info for the phase.
- Parameters:
-
inputFile Name of the input file containing the phase XML data to set up the object id ID of the phase in the input file. Defaults to the empty string.
Definition at line 91 of file HMWSoln.cpp.
Construct and initialize an HMWSoln ThermoPhase object directly from an XML database.
- Parameters:
-
phaseRef XML phase node containing the description of the phase id id attribute containing the name of the phase. (default is the empty string)
Definition at line 142 of file HMWSoln.cpp.
References HMWSoln::elambda, and HMWSoln::elambda1.
Copy Constructor.
Copy constructor for the object. Constructed object will be a clone of this object, but will also own all of its data. This is a wrapper around the assignment operator
- Parameters:
-
right Object to be copied.
Definition at line 199 of file HMWSoln.cpp.
| HMWSoln | ( | int | testProb | ) |
This is a special constructor, used to replicate test problems during the initial verification of the object.
test problems: 1 = NaCl problem - 5 species - the thermo is read in from an XML file
speci molality charge Cl- 6.0954 6.0997E+00 -1 H+ 1.0000E-08 2.1628E-09 1 Na+ 6.0954E+00 6.0997E+00 1 OH- 7.5982E-07 1.3977E-06 -1 HMW_params____beta0MX__beta1MX__beta2MX__CphiMX_____alphaMX__thetaij 10 1 2 0.1775 0.2945 0.0 0.00080 2.0 0.0 1 3 0.0765 0.2664 0.0 0.00127 2.0 0.0 1 4 0.0 0.0 0.0 0.0 0.0 -0.050 2 3 0.0 0.0 0.0 0.0 0.0 0.036 2 4 0.0 0.0 0.0 0.0 0.0 0.0 3 4 0.0864 0.253 0.0 0.0044 2.0 0.0 Triplet_interaction_parameters_psiaa'_or_psicc' 2 1 2 3 -0.004 1 3 4 -0.006
- Parameters:
-
testProb Hard -coded test problem to instantiate. Current valid values are 1.
Definition at line 433 of file HMWSoln.cpp.
References HMWSoln::constructPhaseFile(), HMWSoln::m_Alpha1MX_ij, HMWSoln::m_Beta0MX_ij, HMWSoln::m_Beta1MX_ij, HMWSoln::m_CounterIJ, HMWSoln::m_CphiMX_ij, Phase::m_kk, HMWSoln::m_Psi_ijk, HMWSoln::m_Psi_ijk_coeff, HMWSoln::m_Theta_ij, HMWSoln::printCoeffs(), and Constituents::speciesIndex().
| ~HMWSoln | ( | ) | [virtual] |
Destructor.
Definition at line 579 of file HMWSoln.cpp.
Member Function Documentation
| doublereal _RT | ( | ) | const [inline, inherited] |
Return the Gas Constant multiplied by the current temperature.
The units are Joules kmol-1
Definition at line 1526 of file ThermoPhase.h.
References Cantera::GasConstant, and State::temperature().
Referenced by VPStandardStateTP::getChemPotentials_RT(), IdealSolnGasVPSS::getChemPotentials_RT(), WaterSSTP::getGibbs_ref(), IdealGasPhase::getGibbs_ref(), IdealSolidSolnPhase::getGibbs_RT(), IdealMolalSoln::getPartialMolarEnthalpies(), IdealSolidSolnPhase::getPureGibbs(), IdealGasPhase::getPureGibbs(), ConstDensityThermo::getPureGibbs(), VPStandardStateTP::getStandardChemPotentials(), IdealGasPhase::getStandardChemPotentials(), and IdealGasPhase::getStandardVolumes_ref().
| void _updateStandardStateThermo | ( | ) | const [protected, virtual, inherited] |
Updates the standard state thermodynamic functions at the current T and P of the solution.
For internal use only.
If m_useTmpStandardStateStorage is true, this function must be called for every call to functions in this class.
This function is responsible for updating the following internal members, when m_useTmpStandardStateStorage is true.
- m_hss_RT;
- m_cpss_R;
- m_gss_RT;
- m_sss_R;
- m_Vss
This function doesn't check to see if the temperature or pressure has changed. It automatically assumes that it has changed. If m_useTmpStandardStateStorage is not true, this function may be required to be called by child classes to update internal member data..
Definition at line 492 of file VPStandardStateTP.cpp.
References AssertThrowMsg, VPStandardStateTP::m_Pcurrent, VPStandardStateTP::m_Plast_ss, VPStandardStateTP::m_Tlast_ss, VPStandardStateTP::m_VPSS_ptr, VPSSMgr::setState_TP(), and State::temperature().
Referenced by IdealMolalSoln::getActivities(), DebyeHuckel::getActivities(), DebyeHuckel::getMolalityActivityCoefficients(), DebyeHuckel::setState_TP(), and VPStandardStateTP::updateStandardStateThermo().
| double A_Debye_TP | ( | double | temperature = -1.0, |
|
| double | pressure = -1.0 | |||
| ) | const [virtual] |
Value of the Debye Huckel constant as a function of temperature and pressure.
A_Debye = (F e B_Debye) / (8 Pi epsilon R T)
Units = sqrt(kg/gmol)
- Parameters:
-
temperature Temperature of the derivative calculation or -1 to indicate the current temperature pressure Pressure of the derivative calcualtion or -1 to indicate the current pressure
Definition at line 1412 of file HMWSoln.cpp.
References WaterProps::ADebye(), HMWSoln::m_A_Debye, HMWSoln::m_form_A_Debye, HMWSoln::m_waterProps, HMWSoln::pressure(), and State::temperature().
Referenced by HMWSoln::getUnscaledMolalityActivityCoefficients().
| int activityConvention | ( | ) | const [virtual, inherited] |
This method returns the activity convention.
Currently, there are two activity conventions Molar-based activities Unit activity of species at either a hypothetical pure solution of the species or at a hypothetical pure ideal solution at infinite dilution cAC_CONVENTION_MOLAR 0
- default
Molality based acvtivities (unit activity of solutes at a hypothetical 1 molal solution referenced to infinite dilution at all pressures and temperatures). cAC_CONVENTION_MOLALITY 1
We set the convention to molality here.
Reimplemented from ThermoPhase.
Definition at line 430 of file MolalityVPSSTP.cpp.
References Cantera::cAC_CONVENTION_MOLALITY.
| void addElement | ( | const XML_Node & | e | ) | [inherited] |
Add an element from an XML specification.
- Parameters:
-
e Reference to the XML_Node where the element is described.
Definition at line 138 of file Constituents.cpp.
References Elements::addElement(), and Constituents::m_Elements.
| void addElement | ( | const std::string & | symbol, | |
| doublereal | weight | |||
| ) | [inherited] |
Add an element.
- Parameters:
-
symbol Atomic symbol std::string. weight Atomic mass in amu.
Definition at line 132 of file Constituents.cpp.
References Elements::addElement(), and Constituents::m_Elements.
| void addElementsFromXML | ( | const XML_Node & | phase | ) | [inherited] |
Add all elements referenced in an XML_Node tree.
- Parameters:
-
phase Reference to the top XML_Node of a phase
Definition at line 169 of file Constituents.cpp.
References Elements::addElementsFromXML(), and Constituents::m_Elements.
| void addUniqueElement | ( | const XML_Node & | e | ) | [inherited] |
Adde an element, checking for uniqueness.
The uniqueness is checked by comparing the string symbol. If not unique, nothing is done.
- Parameters:
-
e Reference to the XML_Node where the element is described.
Definition at line 164 of file Constituents.cpp.
References Elements::addUniqueElement(), and Constituents::m_Elements.
| void addUniqueElement | ( | const std::string & | symbol, | |
| doublereal | weight, | |||
| int | atomicNumber = 0, |
|||
| doublereal | entropy298 = ENTROPY298_UNKNOWN | |||
| ) | [inherited] |
Add an element, checking for uniqueness.
The uniqueness is checked by comparing the string symbol. If not unique, nothing is done.
- Parameters:
-
symbol String symbol of the element weight Atomic weight of the element (kg kmol-1). atomicNumber Atomic number of the element (unitless) entropy298 Entropy of the element at 298 K and 1 bar in its most stable form. The default is the value ENTROPY298_UNKNOWN, which is interpreted as an unknown, and if used will cause Cantera to throw an error.
Definition at line 157 of file Constituents.cpp.
References Elements::addUniqueElement(), and Constituents::m_Elements.
| void addUniqueSpecies | ( | const std::string & | name, | |
| const doublereal * | comp, | |||
| doublereal | charge = 0.0, |
|||
| doublereal | size = 1.0 | |||
| ) | [inherited] |
Add a species to the phase, checking for uniqueness of the name.
This routine checks for uniqueness of the string name. It only adds the species if it is unique.
- Parameters:
-
name String name of the species comp Double vector containing the elemental composition of the species. charge Charge of the species. Defaults to zero. size Size of the species (meters). Defaults to 1 meter.
Definition at line 357 of file Constituents.cpp.
References Constituents::m_Elements, Constituents::m_speciesCharge, Constituents::m_speciesComp, Constituents::m_speciesNames, Constituents::m_speciesSize, and Elements::nElements().
| double ADebye_J | ( | double | temperature = -1.0, |
|
| double | pressure = -1.0 | |||
| ) | const |
Return Pitzer's definition of A_J.
This is basically the temperature derivative of A_L, and the second derivative of A_phi
A_Debye = (F e B_Debye) / (8 Pi epsilon R T) dA_phidT = d(A_Debye)/dT / 3.0 A_J = 2 A_L/T + 4 * R * T * T * d2(A_phi)/dT2
Units = sqrt(kg/gmol) (R)
- Parameters:
-
temperature Temperature of the derivative calculation or -1 to indicate the current temperature pressure Pressure of the derivative calcualtion or -1 to indicate the current pressure
Definition at line 1568 of file HMWSoln.cpp.
References HMWSoln::ADebye_L(), HMWSoln::d2A_DebyedT2_TP(), Cantera::GasConstant, and State::temperature().
| double ADebye_L | ( | double | temperature = -1.0, |
|
| double | pressure = -1.0 | |||
| ) | const |
Return Pitzer's definition of A_L.
This is basically the derivative of the A_phi multiplied by 4 R T**2
A_Debye = (F e B_Debye) / (8 Pi epsilon R T) dA_phidT = d(A_Debye)/dT / 3.0 A_L = dA_phidT * (4 * R * T * T)
Units = sqrt(kg/gmol) (RT)
- Parameters:
-
temperature Temperature of the derivative calculation or -1 to indicate the current temperature pressure Pressure of the derivative calcualtion or -1 to indicate the current pressure
Definition at line 1518 of file HMWSoln.cpp.
References HMWSoln::dA_DebyedT_TP(), Cantera::GasConstant, and State::temperature().
Referenced by HMWSoln::ADebye_J().
| double ADebye_V | ( | double | temperature = -1.0, |
|
| double | pressure = -1.0 | |||
| ) | const |
Return Pitzer's definition of A_V.
This is the derivative wrt pressure of A_phi multiplied by - 4 R T
A_Debye = (F e B_Debye) / (8 Pi epsilon R T) dA_phidT = d(A_Debye)/dP / 3.0 A_V = - dA_phidP * (4 * R * T)
Units = sqrt(kg/gmol) (RT) / Pascal
- Parameters:
-
temperature Temperature of the derivative calculation or -1 to indicate the current temperature pressure Pressure of the derivative calcualtion or -1 to indicate the current pressure
Definition at line 1539 of file HMWSoln.cpp.
References HMWSoln::dA_DebyedP_TP(), Cantera::GasConstant, and State::temperature().
| double AionicRadius | ( | int | k = 0 |
) | const |
Reports the ionic radius of the kth species.
- Parameters:
-
k Species index
Definition at line 1621 of file HMWSoln.cpp.
References HMWSoln::m_Aionic.
| void applyphScale | ( | doublereal * | acMolality | ) | const [private, virtual] |
Apply the current phScale to a set of activity Coefficients or activities.
See the Eq3/6 Manual for a thorough discussion.
- Parameters:
-
acMolality input/Output vector containing the molality based activity coefficients. length: m_kk.
Reimplemented from MolalityVPSSTP.
Definition at line 6354 of file HMWSoln.cpp.
References AssertTrace, MolalityVPSSTP::m_indexCLM, HMWSoln::m_lnActCoeffMolal_Unscaled, MolalityVPSSTP::m_pHScalingType, Constituents::m_speciesCharge, Cantera::PHSCALE_NBS, Cantera::PHSCALE_PITZER, and HMWSoln::s_NBS_CLM_lnMolalityActCoeff().
| int atomicNumber | ( | int | m | ) | const [inherited] |
Atomic number of element m.
- Parameters:
-
m Element index
Definition at line 117 of file Constituents.cpp.
References Elements::atomicNumber(), and Constituents::m_Elements.
Referenced by MultiPhase::addPhase().
| doublereal atomicWeight | ( | int | m | ) | const [inherited] |
Atomic weight of element m.
- Parameters:
-
m Element index
Definition at line 95 of file Constituents.cpp.
References Elements::atomicWeight(), and Constituents::m_Elements.
Referenced by WaterSSTP::initThermoXML().
| const vector_fp & atomicWeights | ( | ) | const [inherited] |
Return a read-only reference to the vector of atomic weights.
Definition at line 109 of file Constituents.cpp.
References Elements::atomicWeights(), and Constituents::m_Elements.
| void calc_lambdas | ( | double | is | ) | const [private] |
Calculate the lambda interactions.
Calculate E-lambda terms for charge combinations of like sign, using method of Pitzer (1975).
- Parameters:
-
is Ionic strength
Definition at line 6051 of file HMWSoln.cpp.
References HMWSoln::elambda, HMWSoln::elambda1, and HMWSoln::m_debugCalc.
Referenced by HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
| void calc_thetas | ( | int | z1, | |
| int | z2, | |||
| double * | etheta, | |||
| double * | etheta_prime | |||
| ) | const [private] |
Calculate etheta and etheta_prime.
This interaction will be nonzero for species with the same charge. this routine is not to be called for neutral species; it core dumps or error exits.
MEC implementation routine.
- Parameters:
-
z1 charge of the first molecule z2 charge of the second molecule etheta return pointer containing etheta etheta_prime Return pointer containing etheta_prime.
This routine uses the internal variables, elambda[] and elambda1[].
There is no prohibition against calling
Definition at line 6120 of file HMWSoln.cpp.
References HMWSoln::elambda, and HMWSoln::elambda1.
Referenced by HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
| void calcDensity | ( | ) | [protected, virtual] |
Calculate the density of the mixture using the partial molar volumes and mole fractions as input.
The formula for this is
![\[ \rho = \frac{\sum_k{X_k W_k}}{\sum_k{X_k V_k}} \]](form_91.png)
where 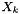 are the mole fractions,
are the mole fractions, 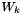 are the molecular weights, and
are the molecular weights, and 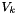 are the pure species molar volumes.
are the pure species molar volumes.
Note, the basis behind this formula is that in an ideal solution the partial molar volumes are equal to the pure species molar volumes. We have additionally specified in this class that the pure species molar volumes are independent of temperature and pressure.
NOTE: This is a non-virtual function, which is not a member of the ThermoPhase base class.
Reimplemented from VPStandardStateTP.
Definition at line 762 of file HMWSoln.cpp.
References HMWSoln::setState_TP(), and State::temperature().
| void calcIMSCutoffParams_ | ( | ) | [private] |
Precalculate the IMS Cutoff parameters for typeCutoff = 2.
Definition at line 1669 of file HMWSoln_input.cpp.
References HMWSoln::IMS_afCut_, HMWSoln::IMS_agCut_, HMWSoln::IMS_bfCut_, HMWSoln::IMS_bgCut_, HMWSoln::IMS_cCut_, HMWSoln::IMS_dfCut_, HMWSoln::IMS_dgCut_, HMWSoln::IMS_efCut_, HMWSoln::IMS_egCut_, HMWSoln::IMS_gamma_k_min_, HMWSoln::IMS_gamma_o_min_, HMWSoln::IMS_slopefCut_, HMWSoln::IMS_slopegCut_, and HMWSoln::IMS_X_o_cutoff_.
Referenced by HMWSoln::initThermoXML().
| void calcMCCutoffParams_ | ( | ) | [private] |
Calculate molality cut-off parameters.
Definition at line 1719 of file HMWSoln_input.cpp.
References HMWSoln::MC_apCut_, HMWSoln::MC_bpCut_, HMWSoln::MC_cpCut_, HMWSoln::MC_dpCut_, HMWSoln::MC_epCut_, HMWSoln::MC_slopepCut_, HMWSoln::MC_X_o_cutoff_, and HMWSoln::MC_X_o_min_.
Referenced by HMWSoln::initThermoXML().
| void calcMolalities | ( | ) | const [inherited] |
Calculates the molality of all species and stores the result internally.
We calculate the vector of molalities of the species in the phase and store the result internally:
![\[ m_i = \frac{X_i}{1000 * M_o * X_{o,p}} \]](form_371.png)
where
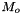 is the molecular weight of the solvent
is the molecular weight of the solvent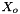 is the mole fraction of the solvent
is the mole fraction of the solvent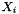 is the mole fraction of the solute.
is the mole fraction of the solute.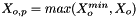
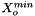 = minimum mole fraction of solvent allowed in the denominator.
= minimum mole fraction of solvent allowed in the denominator.
Definition at line 219 of file MolalityVPSSTP.cpp.
References DATA_PTR, State::getMoleFractions(), MolalityVPSSTP::m_indexSolvent, Phase::m_kk, MolalityVPSSTP::m_Mnaught, MolalityVPSSTP::m_molalities, and MolalityVPSSTP::m_xmolSolventMIN.
Referenced by DebyeHuckel::_lnactivityWaterHelgesonFixedForm(), IdealMolalSoln::getActivities(), IdealMolalSoln::getChemPotentials(), MolalityVPSSTP::getMolalities(), IdealMolalSoln::getPartialMolarEntropies(), DebyeHuckel::s_update_lnMolalityActCoeff(), IdealMolalSoln::s_updateIMS_lnMolalityActCoeff(), HMWSoln::s_updateIMS_lnMolalityActCoeff(), MolalityVPSSTP::setMolalities(), and MolalityVPSSTP::setMolalitiesByName().
| void calcMolalitiesCropped | ( | ) | const [private] |
Calculate the cropped molalities.
This is an internal routine that calculates values of m_molalitiesCropped from m_molalities
Definition at line 1877 of file HMWSoln.cpp.
| doublereal charge | ( | int | k | ) | const [inherited] |
Electrical charge of one species k molecule, divided by the magnitude of the electron charge ( 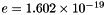 Coulombs). Dimensionless.
Coulombs). Dimensionless.
- Parameters:
-
k species index
Definition at line 266 of file Constituents.cpp.
References Constituents::m_speciesCharge.
Referenced by Phase::chargeDensity(), PDSS_HKFT::constructPDSSXML(), ThermoPhase::getElectrochemPotentials(), MolalityVPSSTP::getElectrochemPotentials(), PDSS_HKFT::initThermo(), DebyeHuckel::initThermoXML(), HMWSoln::readXMLBinarySalt(), HMWSoln::readXMLLambdaNeutral(), HMWSoln::readXMLMunnnNeutral(), HMWSoln::readXMLPsiCommonAnion(), HMWSoln::readXMLPsiCommonCation(), HMWSoln::readXMLThetaAnion(), HMWSoln::readXMLThetaCation(), HMWSoln::readXMLZetaCation(), and MolalityVPSSTP::setMolalitiesByName().
| doublereal chargeDensity | ( | ) | const [inherited] |
Charge density [C/m^3].
Definition at line 334 of file Phase.cpp.
References Constituents::charge(), Phase::moleFraction(), and Constituents::nSpecies().
| bool chargeNeutralityNecessary | ( | ) | const [inline, inherited] |
Returns the chargeNeutralityNecessity boolean.
Some phases must have zero net charge in order for their thermodynamics functions to be valid. If this is so, then the value returned from this function is true. If this is not the case, then this is false. Now, ideal gases have this parameter set to false, while solution with molality-based activity coefficients have this parameter set to true.
Definition at line 2066 of file ThermoPhase.h.
References ThermoPhase::m_chargeNeutralityNecessary.
| void clear | ( | ) | [inherited] |
Remove all elements and species.
| doublereal concentration | ( | const int | k | ) | const [inherited] |
Concentration of species k.
If k is outside the valid range, an exception will be thrown.
- Parameters:
-
k Index of species
Definition at line 134 of file State.cpp.
References State::m_dens, State::m_kk, State::m_rmolwts, and State::m_y.
| void constructPhaseFile | ( | std::string | inputFile, | |
| std::string | id | |||
| ) |
Initialization of a HMWSoln phase using an xml file.
This routine is a precursor to initThermo(XML_Node*) routine, which does most of the work.
- Parameters:
-
inputFile XML file containing the description of the phase id Optional parameter identifying the name of the phase. If none is given, the first XML phase element will be used.
Definition at line 1060 of file HMWSoln_input.cpp.
References XML_Node::build(), HMWSoln::constructPhaseXML(), XML_Node::copy(), Cantera::findInputFile(), Cantera::findXMLPhase(), and Phase::xml().
Referenced by HMWSoln::HMWSoln().
| void constructPhaseXML | ( | XML_Node & | phaseNode, | |
| std::string | id | |||
| ) |
Import and initialize a HMWSoln phase specification in an XML tree into the current object.
Here we read an XML description of the phase. We import descriptions of the elements that make up the species in a phase. We import information about the species, including their reference state thermodynamic polynomials. We then freeze the state of the species.
Then, we read the species molar volumes from the xml tree to finish the initialization.
- Parameters:
-
phaseNode This object must be the phase node of a complete XML tree description of the phase, including all of the species data. In other words while "phase" must point to an XML phase object, it must have sibling nodes "speciesData" that describe the species in the phase. id ID of the phase. If nonnull, a check is done to see if phaseNode is pointing to the phase with the correct id.
Definition at line 1117 of file HMWSoln_input.cpp.
References Cantera::atofCheck(), XML_Node::attrib(), XML_Node::child(), ctml::getStringArray(), XML_Node::hasChild(), XML_Node::id(), Cantera::importPhase(), Cantera::lowercase(), HMWSoln::m_formGC, HMWSoln::m_formPitzer, HMWSoln::m_formPitzerTemp, HMWSoln::m_TempPitzerRef, PITZERFORM_BASE, and Constituents::size().
Referenced by HMWSoln::constructPhaseFile().
| void counterIJ_setup | ( | void | ) | const [private] |
Set up a counter variable for keeping track of symmetric binary interactactions amongst the solute species.
The purpose of this is to squeeze the ij parameters into a compressed single counter.
n = m_kk*i + j m_Counter[n] = counter
Definition at line 2049 of file HMWSoln.cpp.
References HMWSoln::m_CounterIJ.
Referenced by HMWSoln::initLengths(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
| doublereal cp_mass | ( | ) | const [inline, inherited] |
Specific heat at constant pressure.
Units: J/kg/K.
Definition at line 1510 of file ThermoPhase.h.
References ThermoPhase::cp_mole(), and State::meanMolecularWeight().
Referenced by ThermoPhase::report(), PureFluidPhase::report(), MolalityVPSSTP::report(), SingleSpeciesTP::setState_HP(), ThermoPhase::setState_HPorUV(), SingleSpeciesTP::setState_SP(), and ThermoPhase::setState_SPorSV().
| doublereal cp_mole | ( | ) | const [virtual] |
Molar heat capacity at constant pressure. Units: J/kmol/K.
Reimplemented from ThermoPhase.
Definition at line 726 of file HMWSoln.cpp.
| virtual doublereal critDensity | ( | ) | const [inline, virtual] |
Critical density (kg/m3).
Reimplemented from ThermoPhase.
Definition at line 2006 of file HMWSoln.h.
References HMWSoln::err().
| virtual doublereal critPressure | ( | ) | const [inline, virtual] |
Critical pressure (Pa).
Reimplemented from ThermoPhase.
Definition at line 2001 of file HMWSoln.h.
References HMWSoln::err().
| virtual doublereal critTemperature | ( | ) | const [inline, virtual] |
Critical temperature (K).
Reimplemented from ThermoPhase.
Definition at line 1996 of file HMWSoln.h.
References HMWSoln::err().
| doublereal cv_mass | ( | ) | const [inline, inherited] |
Specific heat at constant volume.
Units: J/kg/K.
Definition at line 1517 of file ThermoPhase.h.
References ThermoPhase::cv_mole(), and State::meanMolecularWeight().
Referenced by ThermoPhase::report(), PureFluidPhase::report(), MolalityVPSSTP::report(), ThermoPhase::setState_HPorUV(), ThermoPhase::setState_SPorSV(), SingleSpeciesTP::setState_SV(), and SingleSpeciesTP::setState_UV().
| doublereal cv_mole | ( | ) | const [virtual] |
Molar heat capacity at constant volume. Units: J/kmol/K.
Reimplemented from ThermoPhase.
Definition at line 733 of file HMWSoln.cpp.
References DATA_PTR, HMWSoln::getPartialMolarCp(), HMWSoln::m_tmpV, and State::mean_X().
| double d2A_DebyedT2_TP | ( | double | temperature = -1.0, |
|
| double | pressure = -1.0 | |||
| ) | const [virtual] |
Value of the 2nd derivative of the Debye Huckel constant with respect to temperature as a function of temperature and pressure.
A_Debye = (F e B_Debye) / (8 Pi epsilon R T)
Units = sqrt(kg/gmol)
- Parameters:
-
temperature Temperature of the derivative calculation or -1 to indicate the current temperature pressure Pressure of the derivative calcualtion or -1 to indicate the current pressure
Definition at line 1590 of file HMWSoln.cpp.
References WaterProps::ADebye(), HMWSoln::m_form_A_Debye, HMWSoln::m_waterProps, HMWSoln::pressure(), and State::temperature().
Referenced by HMWSoln::ADebye_J(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
| double dA_DebyedP_TP | ( | double | temperature = -1.0, |
|
| double | pressure = -1.0 | |||
| ) | const [virtual] |
Value of the derivative of the Debye Huckel constant with respect to pressure, as a function of temperature and pressure.
A_Debye = (F e B_Debye) / (8 Pi epsilon R T)
Units = sqrt(kg/gmol)
- Parameters:
-
temperature Temperature of the derivative calculation or -1 to indicate the current temperature pressure Pressure of the derivative calcualtion or -1 to indicate the current pressure
Definition at line 1483 of file HMWSoln.cpp.
References WaterProps::ADebye(), HMWSoln::m_form_A_Debye, HMWSoln::m_waterProps, HMWSoln::pressure(), and State::temperature().
Referenced by HMWSoln::ADebye_V(), HMWSoln::debugPrinting(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
| double dA_DebyedT_TP | ( | double | temperature = -1.0, |
|
| double | pressure = -1.0 | |||
| ) | const [virtual] |
Value of the derivative of the Debye Huckel constant with respect to temperature as a function of temperature and pressure.
A_Debye = (F e B_Debye) / (8 Pi epsilon R T)
Units = sqrt(kg/gmol)
- Parameters:
-
temperature Temperature of the derivative calculation or -1 to indicate the current temperature pressure Pressure of the derivative calcualtion or -1 to indicate the current pressure
Definition at line 1448 of file HMWSoln.cpp.
References WaterProps::ADebye(), HMWSoln::m_form_A_Debye, HMWSoln::m_waterProps, HMWSoln::pressure(), and State::temperature().
Referenced by HMWSoln::ADebye_L(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
| int debugPrinting | ( | ) |
Return int specifying the amount of debug printing.
This will return 0 if DEBUG_MODE is not turned on
Definition at line 6491 of file HMWSoln.cpp.
References HMWSoln::dA_DebyedP_TP(), and HMWSoln::m_IionicMolality.
| double density | ( | ) | const [virtual] |
Returns the current value of the density.
- Returns:
- value of the density. Units: kg/m^3
Reimplemented from State.
Definition at line 808 of file HMWSoln.cpp.
Referenced by HMWSoln::setDensity().
| ThermoPhase * duplMyselfAsThermoPhase | ( | ) | const [virtual] |
Duplicator from the ThermoPhase parent class.
Given a pointer to a ThermoPhase object, this function will duplicate the ThermoPhase object and all underlying structures. This is basically a wrapper around the copy constructor.
- Returns:
- returns a pointer to a ThermoPhase
Reimplemented from MolalityVPSSTP.
Definition at line 592 of file HMWSoln.cpp.
References HMWSoln::HMWSoln().
| doublereal electricPotential | ( | ) | const [inline, inherited] |
Returns the electric potential of this phase (V).
Units are Volts (which are Joules/coulomb)
Reimplemented in IdealMolalSoln.
Definition at line 1003 of file ThermoPhase.h.
References ThermoPhase::m_phi.
Referenced by ThermoPhase::getElectrochemPotentials(), MolalityVPSSTP::getElectrochemPotentials(), ThermoPhase::report(), PureFluidPhase::report(), and MolalityVPSSTP::report().
| int elementIndex | ( | std::string | name | ) | const [inherited] |
Index of element named 'name'.
The index is an integer assigned to each element in the order it was added, beginning with 0 for the first element.
- Parameters:
-
name name of the element
If 'name' is not the name of an element in the set, then the value -1 is returned.
Definition at line 197 of file Constituents.cpp.
References Elements::elementIndex(), and Constituents::m_Elements.
Referenced by MultiPhase::init(), WaterSSTP::initThermoXML(), and PDSS_HKFT::LookupGe().
| string elementName | ( | int | m | ) | const [inherited] |
Name of the element with index m.
This is a passthrough routine to the Element object.
- Parameters:
-
m Element index.
- Exceptions:
-
If m < 0 or m >= nElements(), the exception, ElementRangeError, is thrown.
Definition at line 209 of file Constituents.cpp.
References Elements::elementName(), and Constituents::m_Elements.
Referenced by MultiPhase::addPhase(), PDSS_HKFT::convertDGFormation(), and MolalityVPSSTP::findCLMIndex().
| const vector< string > & elementNames | ( | ) | const [inherited] |
Return a read-only reference to the vector of element names.
Definition at line 229 of file Constituents.cpp.
References Elements::elementNames(), and Constituents::m_Elements.
| bool elementsFrozen | ( | ) | [inherited] |
True if freezeElements has been called.
Definition at line 183 of file Constituents.cpp.
References Elements::elementsFrozen(), and Constituents::m_Elements.
| doublereal enthalpy_mass | ( | ) | const [inline, inherited] |
Specific enthalpy.
Units: J/kg.
Definition at line 1482 of file ThermoPhase.h.
References ThermoPhase::enthalpy_mole(), and State::meanMolecularWeight().
Referenced by ThermoPhase::report(), PureFluidPhase::report(), MolalityVPSSTP::report(), SingleSpeciesTP::setState_HP(), ThermoPhase::setState_HPorUV(), and ThermoPhase::setState_SPorSV().
| doublereal enthalpy_mole | ( | ) | const [virtual] |
Molar enthalpy. Units: J/kmol.
Molar enthalpy of the solution. Units: J/kmol. (HKM -> Bump up to Parent object)
Reimplemented from ThermoPhase.
Definition at line 627 of file HMWSoln.cpp.
Referenced by HMWSoln::intEnergy_mole().
| doublereal entropy_mass | ( | ) | const [inline, inherited] |
Specific entropy.
Units: J/kg/K.
Definition at line 1496 of file ThermoPhase.h.
References ThermoPhase::entropy_mole(), and State::meanMolecularWeight().
Referenced by ThermoPhase::report(), PureFluidPhase::report(), MolalityVPSSTP::report(), SingleSpeciesTP::setState_SP(), ThermoPhase::setState_SPorSV(), and SingleSpeciesTP::setState_SV().
| doublereal entropy_mole | ( | ) | const [virtual] |
Molar entropy. Units: J/kmol/K.
Molar entropy of the solution. Units: J/kmol/K. For an ideal, constant partial molar volume solution mixture with pure species phases which exhibit zero volume expansivity:
![\[ \hat s(T, P, X_k) = \sum_k X_k \hat s^0_k(T) - \hat R \sum_k X_k log(X_k) \]](form_89.png)
The reference-state pure-species entropies 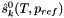 are computed by the species thermodynamic property manager. The pure species entropies are independent of temperature since the volume expansivities are equal to zero.
are computed by the species thermodynamic property manager. The pure species entropies are independent of temperature since the volume expansivities are equal to zero.
- See also:
- SpeciesThermo
(HKM -> Bump up to Parent object)
Reimplemented from ThermoPhase.
Definition at line 710 of file HMWSoln.cpp.
| doublereal entropyElement298 | ( | int | m | ) | const [inherited] |
Entropy of the element in its standard state at 298 K and 1 bar.
- Parameters:
-
m Element index
Definition at line 100 of file Constituents.cpp.
References Elements::entropyElement298(), and Constituents::m_Elements.
Referenced by PDSS_HKFT::LookupGe().
| int eosType | ( | ) | const [virtual] |
Equation of state type flag.
The base class returns zero. Subclasses should define this to return a unique non-zero value. Constants defined for this purpose are listed in mix_defs.h.
Reimplemented from MolalityVPSSTP.
Definition at line 603 of file HMWSoln.cpp.
References HMWSoln::m_formGC.
| doublereal err | ( | std::string | msg | ) | const [private] |
Local error routine.
Bail out of functions with an error exit if they are not implemented.
- Parameters:
-
msg print out a message and error exit
Reimplemented from MolalityVPSSTP.
Definition at line 1633 of file HMWSoln.cpp.
Referenced by HMWSoln::critDensity(), HMWSoln::critPressure(), HMWSoln::critTemperature(), HMWSoln::satTemperature(), HMWSoln::setState_Psat(), HMWSoln::setState_Tsat(), HMWSoln::setToEquilState(), and HMWSoln::vaporFraction().
| int formPitzer | ( | ) | const [inline] |
Returns the form of the Pitzer parameterization used
Definition at line 2298 of file HMWSoln.h.
References HMWSoln::m_formPitzer.
| void freezeElements | ( | ) | [inherited] |
Prohibit addition of more elements, and prepare to add species.
Definition at line 176 of file Constituents.cpp.
References Elements::freezeElements(), and Constituents::m_Elements.
| void freezeSpecies | ( | ) | [virtual, inherited] |
Finished adding species, prepare to use them for calculation of mixture properties.
Reimplemented from Constituents.
Definition at line 348 of file Phase.cpp.
References State::init(), Phase::m_data, Phase::m_kk, Constituents::molecularWeights(), and Constituents::nSpecies().
| void getActivities | ( | doublereal * | ac | ) | const [virtual] |
Get the array of non-dimensional activities at the current solution temperature, pressure, and solution concentration.
We resolve this function at this level by calling on the activityConcentration function. However, derived classes may want to override this default implementation.
(note solvent is on molar scale).
- Parameters:
-
ac Output vector of activities. Length: m_kk.
Reimplemented from MolalityVPSSTP.
Definition at line 1004 of file HMWSoln.cpp.
References MolalityVPSSTP::m_indexSolvent, HMWSoln::m_lnActCoeffMolal_Scaled, MolalityVPSSTP::m_molalities, Phase::moleFraction(), HMWSoln::s_update_lnMolalityActCoeff(), and VPStandardStateTP::updateStandardStateThermo().
Referenced by HMWSoln::getActivityConcentrations().
| void getActivityCoefficients | ( | doublereal * | ac | ) | const [virtual, inherited] |
Get the array of non-dimensional activity coefficients at the current solution temperature, pressure, and solution concentration.
These are mole-fraction based activity coefficients. In this object, their calculation is based on translating the values of the molality-based activity coefficients. See Denbigh p. 278 for a thorough discussion.
The molar-based activity coefficients 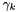 may be calculated from the molality-based activity coefficients,
may be calculated from the molality-based activity coefficients, 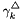 by the following formula.
by the following formula.
![\[ \gamma_k = \frac{\gamma_k^\triangle}{X_o} \]](form_366.png)
For purposes of establishing a convention, the molar activity coefficient of the solvent is set equal to the molality-based activity coefficient of the solvent:
![\[ \gamma_o = \gamma_o^\triangle \]](form_367.png)
Derived classes don't need to overload this function. This function is handled at this level.
- Parameters:
-
ac Output vector containing the mole-fraction based activity coefficients. length: m_kk.
Reimplemented from ThermoPhase.
Definition at line 465 of file MolalityVPSSTP.cpp.
References AssertThrow, MolalityVPSSTP::getMolalityActivityCoefficients(), MolalityVPSSTP::m_indexSolvent, Phase::m_kk, MolalityVPSSTP::m_xmolSolventMIN, and Phase::moleFraction().
| void getActivityConcentrations | ( | doublereal * | c | ) | const [virtual] |
This method returns an array of generalized activity concentrations.
The generalized activity concentrations, 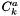 , are defined such that
, are defined such that 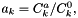 where
where 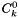 is a standard concentration defined below. These generalized concentrations are used by kinetics manager classes to compute the forward and reverse rates of elementary reactions.
is a standard concentration defined below. These generalized concentrations are used by kinetics manager classes to compute the forward and reverse rates of elementary reactions.
The generalized activity concentration of a solute species has the following form
![\[ C_j^a = C^o_o \frac{\gamma_j^\triangle n_j}{n_o} \]](form_215.png)
The generalized activity concentration of the solvent has the same units, but its a simpler form
![\[ C_o^a = C^o_o a_o \]](form_216.png)
- Parameters:
-
c Array of generalized concentrations. The units are kmol m-3 for both the solvent and the solute species
Reimplemented from MolalityVPSSTP.
Definition at line 912 of file HMWSoln.cpp.
References HMWSoln::getActivities(), and HMWSoln::standardConcentration().
| void getAtoms | ( | int | k, | |
| double * | atomArray | |||
| ) | const [inherited] |
Get a vector containing the atomic composition of species k.
- Parameters:
-
k species index atomArray vector containing the atomic number in the species. Length: m_mm
Definition at line 480 of file Constituents.cpp.
References Constituents::m_Elements, Constituents::m_speciesComp, and Elements::nElements().
| void getChemPotentials | ( | doublereal * | mu | ) | const [virtual] |
Get the species chemical potentials. Units: J/kmol.
This function returns a vector of chemical potentials of the species in solution.
![\[ \mu_k = \mu^{\triangle}_k(T,P) + R T ln(\gamma_k^{\triangle} m_k) \]](form_102.png)
- Parameters:
-
mu Output vector of species chemical potentials. Length: m_kk. Units: J/kmol
Reimplemented from ThermoPhase.
Definition at line 1068 of file HMWSoln.cpp.
References Cantera::GasConstant, VPStandardStateTP::getStandardChemPotentials(), MolalityVPSSTP::m_indexSolvent, HMWSoln::m_lnActCoeffMolal_Scaled, MolalityVPSSTP::m_molalities, MAX, Phase::moleFraction(), HMWSoln::s_update_lnMolalityActCoeff(), and State::temperature().
| void getChemPotentials_RT | ( | doublereal * | mu | ) | const [virtual, inherited] |
Get the array of non-dimensional species chemical potentials These are partial molar Gibbs free energies.
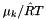 . Units: unitless
. Units: unitless
We close the loop on this function, here, calling getChemPotentials() and then dividing by RT. No need for child classes to handle.
- Parameters:
-
mu Output vector of non-dimensional species chemical potentials Length: m_kk.
Reimplemented from ThermoPhase.
Reimplemented in IdealSolnGasVPSS.
Definition at line 198 of file VPStandardStateTP.cpp.
References ThermoPhase::_RT(), ThermoPhase::getChemPotentials(), and Phase::m_kk.
| void getConcentrations | ( | doublereal *const | c | ) | const [inherited] |
Get the species concentrations (kmol/m^3).
- Parameters:
-
c On return, c contains the concentrations for all species. Array c must have a length greater than or equal to the number of species.
Definition at line 219 of file State.cpp.
References State::m_dens, State::m_ym, and Cantera::scale().
Referenced by ConstDensityThermo::getActivityCoefficients(), SurfPhase::getActivityConcentrations(), IdealSolnGasVPSS::getActivityConcentrations(), IdealGasPhase::getActivityConcentrations(), and SurfPhase::getCoverages().
| void getCp_R | ( | doublereal * | cpr | ) | const [virtual, inherited] |
Get the nondimensional Heat Capacities at constant pressure for the standard state of the species at the current T and P.
This is redefined here to call the internal function, _updateStandardStateThermo(), which calculates all standard state properties at the same time.
- Parameters:
-
cpr Output vector containing the the nondimensional Heat Capacities at constant pressure for the standard state of the species. Length: m_kk.
Reimplemented from ThermoPhase.
Definition at line 261 of file VPStandardStateTP.cpp.
References VPSSMgr::getCp_R(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
Referenced by IdealSolnGasVPSS::getPartialMolarCp(), IdealMolalSoln::getPartialMolarCp(), HMWSoln::getPartialMolarCp(), and DebyeHuckel::getPartialMolarCp().
| void getCp_R_ref | ( | doublereal * | cprt | ) | const [virtual, inherited] |
Returns the vector of nondimensional constant pressure heat capacities of the reference state at the current temperature of the solution and reference pressure for the species.
- Parameters:
-
cprt Output vector contains the nondimensional heat capacities of the species in their reference states length: m_kk, units: dimensionless.
Reimplemented from ThermoPhase.
Definition at line 330 of file VPStandardStateTP.cpp.
References VPSSMgr::getCp_R_ref(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
| virtual void getdlnActCoeffdlnC | ( | doublereal * | dlnActCoeffdlnC | ) | const [inline, virtual, inherited] |
Get the array of log concentration-like derivatives of the log activity coefficients.
This function is a virtual method. For ideal mixtures (unity activity coefficients), this can return zero. Implementations should take the derivative of the logarithm of the activity coefficient with respect to the logarithm of the concentration-like variable (i.e. mole fraction, molality, etc.) that represents the standard state. This quantity is to be used in conjunction with derivatives of that concentration-like variable when the derivative of the chemical potential is taken.
units = dimensionless
- Parameters:
-
dlnActCoeffdlnC Output vector of derivatives of the log Activity Coefficients. length = m_kk
Reimplemented from ThermoPhase.
Definition at line 141 of file VPStandardStateTP.h.
References VPStandardStateTP::err().
| void getElectrochemPotentials | ( | doublereal * | mu | ) | const [inherited] |
Get the species electrochemical potentials.
These are partial molar quantities. This method adds a term 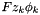 to the to each chemical potential.
to the to each chemical potential.
Units: J/kmol
- Parameters:
-
mu output vector containing the species electrochemical potentials. Length: m_kk.
Reimplemented from ThermoPhase.
Definition at line 530 of file MolalityVPSSTP.cpp.
References Constituents::charge(), ThermoPhase::electricPotential(), ThermoPhase::getChemPotentials(), and Phase::m_kk.
| bool getElementPotentials | ( | doublereal * | lambda | ) | const [inherited] |
Returns the element potentials storred in the ThermoPhase object.
Returns the storred element potentials. The element potentials are retrieved from their storred dimensionless forms by multiplying by RT.
- Parameters:
-
lambda Output vector containing the element potentials. Length = nElements. Units are Joules/kmol.
- Returns:
- bool indicating whether thare are any valid storred element potentials. The calling routine should check this bool. In the case that there aren't any, lambda is not touched.
Definition at line 1015 of file ThermoPhase.cpp.
References Cantera::GasConstant, ThermoPhase::m_hasElementPotentials, ThermoPhase::m_lambdaRRT, Constituents::nElements(), and State::temperature().
| void getEnthalpy_RT | ( | doublereal * | hrt | ) | const [inline, virtual, inherited] |
Get the nondimensional Enthalpy functions for the species at their standard states at the current T and P of the solution.
- Parameters:
-
hrt Output vector of standard state enthalpies. length = m_kk. units are unitless.
Reimplemented from ThermoPhase.
Definition at line 218 of file VPStandardStateTP.cpp.
References VPSSMgr::getEnthalpy_RT(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
Referenced by IdealSolnGasVPSS::getPartialMolarEnthalpies(), IdealMolalSoln::getPartialMolarEnthalpies(), HMWSoln::getPartialMolarEnthalpies(), and DebyeHuckel::getPartialMolarEnthalpies().
| void getEnthalpy_RT_ref | ( | doublereal * | hrt | ) | const [virtual, inherited] |
Returns the vector of nondimensional enthalpies of the reference state at the current temperature of the solution and the reference pressure for the species.
There are also temporary variables for holding the species reference-state values of Cp, H, S, and V at the last temperature and reference pressure called. These functions are not recalculated if a new call is made using the previous temperature. All calculations are done within the routine _updateRefStateThermo().
- Parameters:
-
hrt Output vector contains the nondimensional enthalpies of the reference state of the species length = m_kk, units = dimensionless.
Reimplemented from ThermoPhase.
Definition at line 280 of file VPStandardStateTP.cpp.
References VPSSMgr::getEnthalpy_RT_ref(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
| void getEntropy_R | ( | doublereal * | sr | ) | const [virtual, inherited] |
Get the array of nondimensional Enthalpy functions for the standard state species at the current T and P of the solution.
- Parameters:
-
sr Output vector of nondimensional standard state entropies. length = m_kk.
Reimplemented from ThermoPhase.
Definition at line 239 of file VPStandardStateTP.cpp.
References VPSSMgr::getEntropy_R(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
Referenced by IdealSolnGasVPSS::getPartialMolarEntropies(), IdealMolalSoln::getPartialMolarEntropies(), HMWSoln::getPartialMolarEntropies(), and DebyeHuckel::getPartialMolarEntropies().
| void getEntropy_R_ref | ( | doublereal * | er | ) | const [virtual, inherited] |
Returns the vector of nondimensional entropies of the reference state at the current temperature of the solution and the reference pressure for the species.
- Parameters:
-
er Output vector contain the nondimensional entropies of the species in their reference states length: m_kk, units: dimensionless.
Reimplemented from ThermoPhase.
Definition at line 319 of file VPStandardStateTP.cpp.
References VPSSMgr::getEntropy_R_ref(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
| void getGibbs_ref | ( | doublereal * | g | ) | const [virtual, inherited] |
Returns the vector of the gibbs function of the reference state at the current temperature of the solution and the reference pressure for the species. units = J/kmol
- Parameters:
-
g Output vector contain the Gibbs free energies of the reference state of the species length = m_kk, units = J/kmol.
Reimplemented from ThermoPhase.
Definition at line 304 of file VPStandardStateTP.cpp.
References VPSSMgr::getGibbs_ref(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
| void getGibbs_RT | ( | doublereal * | grt | ) | const [inline, virtual, inherited] |
Get the nondimensional Gibbs functions for the species at their standard states of solution at the current T and P of the solution.
- Parameters:
-
grt Output vector of nondimensional standard state Gibbs free energies. length = m_kk.
Reimplemented from ThermoPhase.
Definition at line 245 of file VPStandardStateTP.cpp.
References VPSSMgr::getGibbs_RT(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
Referenced by VPStandardStateTP::getStandardChemPotentials().
| void getGibbs_RT_ref | ( | doublereal * | grt | ) | const [virtual, inherited] |
Returns the vector of nondimensional Gibbs free energies of the reference state at the current temperature of the solution and the reference pressure for the species.
- Parameters:
-
grt Output vector contains the nondimensional Gibbs free energies of the reference state of the species length = m_kk, units = dimensionless.
Reimplemented from ThermoPhase.
Definition at line 290 of file VPStandardStateTP.cpp.
References VPSSMgr::getGibbs_RT_ref(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
| void getIntEnergy_RT | ( | doublereal * | urt | ) | const [virtual, inherited] |
Returns the vector of nondimensional internal Energies of the standard state at the current temperature and pressure of the solution for each species.
![\[ u^{ss}_k(T,P) = h^{ss}_k(T) - P * V^{ss}_k \]](form_481.png)
- Parameters:
-
urt Output vector of nondimensional standard state internal energies. length = m_kk.
Reimplemented from ThermoPhase.
Definition at line 256 of file VPStandardStateTP.cpp.
References VPSSMgr::getIntEnergy_RT(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
Referenced by IdealSolnGasVPSS::getPartialMolarIntEnergies().
| virtual void getIntEnergy_RT_ref | ( | doublereal * | urt | ) | const [inline, virtual, inherited] |
Returns the vector of nondimensional internal Energies of the reference state at the current temperature of the solution and the reference pressure for each species.
- Parameters:
-
urt Output vector of nondimensional reference state internal energies of the species. Length: m_kk
Reimplemented in IdealGasPhase, IdealSolidSolnPhase, MetalSHEelectrons, MineralEQ3, and StoichSubstanceSSTP.
Definition at line 1424 of file ThermoPhase.h.
References ThermoPhase::err().
| void getMassFractions | ( | doublereal *const | y | ) | const [inherited] |
Get the species mass fractions.
- Parameters:
-
y On return, y contains the mass fractions. Array y must have a length greater than or equal to the number of species. y Output vector of mass fractions. Length is m_kk.
Definition at line 235 of file State.cpp.
References State::m_y.
Referenced by ThermoPhase::report(), PureFluidPhase::report(), and Phase::saveState().
| void getMolalities | ( | doublereal *const | molal | ) | const [inherited] |
This function will return the molalities of the species.
We calculate the vector of molalities of the species in the phase
![\[ m_i = \frac{X_i}{1000 * M_o * X_{o,p}} \]](form_371.png)
where
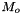 is the molecular weight of the solvent
is the molecular weight of the solvent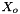 is the mole fraction of the solvent
is the mole fraction of the solvent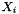 is the mole fraction of the solute.
is the mole fraction of the solute.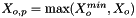
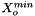 = minimum mole fraction of solvent allowed in the denominator.
= minimum mole fraction of solvent allowed in the denominator.
- Parameters:
-
molal Output vector of molalities. Length: m_kk.
Definition at line 246 of file MolalityVPSSTP.cpp.
References MolalityVPSSTP::calcMolalities(), Phase::m_kk, and MolalityVPSSTP::m_molalities.
Referenced by MolalityVPSSTP::report(), and vcs_MultiPhaseEquil::reportCSV().
| void getMolalityActivityCoefficients | ( | doublereal * | acMolality | ) | const [virtual, inherited] |
Get the array of non-dimensional molality based activity coefficients at the current solution temperature, pressure, and solution concentration.
See Denbigh p. 278 for a thorough discussion. This class must be overwritten in classes which derive from MolalityVPSSTP. This function takes over from the molar-based activity coefficient calculation, getActivityCoefficients(), in derived classes.
These molality based activity coefficients are scaled according to the current pH scale. See the Eq3/6 manual for details.
Activity coefficients for species k may be altered between scales s1 to s2 using the following formula
![\[ ln(\gamma_k^{s2}) = ln(\gamma_k^{s1}) + \frac{z_k}{z_j} \left( ln(\gamma_j^{s2}) - ln(\gamma_j^{s1}) \right) \]](form_369.png)
where j is any one species. For the NBS scale, j is equal to the Cl- species and
![\[ ln(\gamma_{Cl-}^{s2}) = \frac{-A_{\phi} \sqrt{I}}{1.0 + 1.5 \sqrt{I}} \]](form_370.png)
- Parameters:
-
acMolality Output vector containing the molality based activity coefficients. length: m_kk.
Reimplemented in DebyeHuckel, and IdealMolalSoln.
Definition at line 491 of file MolalityVPSSTP.cpp.
References MolalityVPSSTP::applyphScale(), and MolalityVPSSTP::getUnscaledMolalityActivityCoefficients().
Referenced by MolalityVPSSTP::getActivityCoefficients(), and MolalityVPSSTP::report().
| void getMolecularWeights | ( | doublereal * | weights | ) | const [inherited] |
Copy the vector of molecular weights into array weights.
- Parameters:
-
weights Output array of molecular weights (kg/kmol)
Definition at line 289 of file Phase.cpp.
References Phase::molecularWeights().
| void getMolecularWeights | ( | int | iwt, | |
| doublereal * | weights | |||
| ) | const [inherited] |
Copy the vector of molecular weights into array weights.
- Parameters:
-
iwt Unused. weights Output array of molecular weights (kg/kmol)
Definition at line 281 of file Phase.cpp.
References Phase::molecularWeights().
| void getMolecularWeights | ( | vector_fp & | weights | ) | const [inherited] |
Copy the vector of molecular weights into vector weights.
- Parameters:
-
weights Output vector of molecular weights (kg/kmol)
Definition at line 271 of file Phase.cpp.
References Phase::molecularWeights().
| void getMoleFractions | ( | doublereal *const | x | ) | const [inherited] |
Get the species mole fraction vector.
- Parameters:
-
x On return, x contains the mole fractions. Must have a length greater than or equal to the number of species.
Definition at line 231 of file State.cpp.
References State::m_mmw, State::m_ym, and Cantera::scale().
Referenced by IdealMolalSoln::calcDensity(), DebyeHuckel::calcDensity(), MolalityVPSSTP::calcMolalities(), IdealMolalSoln::enthalpy_mole(), LatticePhase::getActivityCoefficients(), HMWSoln::relative_enthalpy(), ThermoPhase::report(), PureFluidPhase::report(), MolalityVPSSTP::report(), MolalityVPSSTP::setMolalitiesByName(), MultiPhase::setMoles(), ThermoPhase::setReferenceComposition(), and MultiPhase::uploadMoleFractionsFromPhases().
| void getMoleFractionsByName | ( | compositionMap & | x | ) | const [inherited] |
Get the mole fractions by name.
- Parameters:
-
x Output composition map containing the species mole fractions.
Definition at line 306 of file Phase.cpp.
References Phase::moleFraction(), Constituents::nSpecies(), and Constituents::speciesName().
| void getParameters | ( | int & | n, | |
| doublereal *const | c | |||
| ) | const [virtual] |
Get the equation of state parameters in a vector.
For internal use only.
The number and meaning of these depends on the subclass.
- Parameters:
-
n number of parameters c array of n coefficients
Reimplemented from ThermoPhase.
Definition at line 1340 of file HMWSoln.cpp.
| void getPartialMolarCp | ( | doublereal * | cpbar | ) | const [virtual] |
Return an array of partial molar heat capacities for the species in the mixture.
Units: J/kmol/K
The following formulas are implemented within the code.
![\[ \bar C_{p,k}(T,P) = C^{\triangle}_{p,k}(T,P) - 2 R T \frac{d \ln( \gamma^{\triangle}_k)}{dT} - R T^2 \frac{d^2 \ln(\gamma^{\triangle}_k) }{{dT}^2} \]](form_205.png)
![\[ \bar C_{p,o}(T,P) = C^o_{p,o}(T,P) - 2 R T \frac{d \ln(a_o)}{dT} - R T^2 \frac{d^2 \ln(a_o)}{{dT}^2} \]](form_206.png)
- Parameters:
-
cpbar Output vector of species partial molar heat capacities at constant pressure. Length = m_kk. units are J/kmol/K.
Reimplemented from ThermoPhase.
Definition at line 1272 of file HMWSoln.cpp.
References Cantera::GasConstant, VPStandardStateTP::getCp_R(), HMWSoln::m_d2lnActCoeffMolaldT2_Scaled, HMWSoln::m_dlnActCoeffMolaldT_Scaled, HMWSoln::s_update_d2lnMolalityActCoeff_dT2(), HMWSoln::s_update_dlnMolalityActCoeff_dT(), HMWSoln::s_update_lnMolalityActCoeff(), and State::temperature().
Referenced by HMWSoln::cv_mole().
| void getPartialMolarEnthalpies | ( | doublereal * | hbar | ) | const [virtual] |
Returns an array of partial molar enthalpies for the species in the mixture.
Units (J/kmol)
For this phase, the partial molar enthalpies are equal to the standard state enthalpies modified by the derivative of the molality-based activity coefficent wrt temperature
![\[ \bar h_k(T,P) = h^{\triangle}_k(T,P) - R T^2 \frac{d \ln(\gamma_k^\triangle)}{dT} \]](form_103.png)
The solvent partial molar enthalpy is equal to
![\[ \bar h_o(T,P) = h^{o}_o(T,P) - R T^2 \frac{d \ln(a_o)}{dT} = h^{o}_o(T,P) + R T^2 (\sum_{k \neq o} m_k) \tilde{M_o} (\frac{d \phi}{dT}) \]](form_201.png)
- Parameters:
-
hbar Output vector of species partial molar enthalpies. Length: m_kk. units are J/kmol.
Reimplemented from ThermoPhase.
Definition at line 1119 of file HMWSoln.cpp.
References Cantera::GasConstant, VPStandardStateTP::getEnthalpy_RT(), HMWSoln::m_dlnActCoeffMolaldT_Scaled, HMWSoln::s_update_dlnMolalityActCoeff_dT(), HMWSoln::s_update_lnMolalityActCoeff(), and State::temperature().
Referenced by HMWSoln::relative_enthalpy().
| void getPartialMolarEntropies | ( | doublereal * | sbar | ) | const [virtual] |
Returns an array of partial molar entropies of the species in the solution.
Units: J/kmol/K.
Maxwell's equations provide an answer for how calculate this (p.215 Smith and Van Ness)
d(chemPot_i)/dT = -sbar_i
For this phase, the partial molar entropies are equal to the SS species entropies plus the ideal solution contribution plus complicated functions of the temperature derivative of the activity coefficents.
![\[ \bar s_k(T,P) = s^{\triangle}_k(T,P) - R \ln( \gamma^{\triangle}_k \frac{m_k}{m^{\triangle}})) - R T \frac{d \ln(\gamma^{\triangle}_k) }{dT} \]](form_202.png)
![\[ \bar s_o(T,P) = s^o_o(T,P) - R \ln(a_o) - R T \frac{d \ln(a_o)}{dT} \]](form_203.png)
- Parameters:
-
sbar Output vector of species partial molar entropies. Length = m_kk. units are J/kmol/K.
Reimplemented from ThermoPhase.
Definition at line 1174 of file HMWSoln.cpp.
References Cantera::fmaxx(), Cantera::GasConstant, VPStandardStateTP::getEntropy_R(), HMWSoln::m_dlnActCoeffMolaldT_Scaled, MolalityVPSSTP::m_indexSolvent, HMWSoln::m_lnActCoeffMolal_Scaled, MolalityVPSSTP::m_molalities, Phase::moleFraction(), HMWSoln::s_update_dlnMolalityActCoeff_dT(), HMWSoln::s_update_lnMolalityActCoeff(), Cantera::SmallNumber, and State::temperature().
Referenced by HMWSoln::gibbs_mole().
| virtual void getPartialMolarIntEnergies | ( | doublereal * | ubar | ) | const [inline, virtual, inherited] |
Return an array of partial molar internal energies for the species in the mixture.
Units: J/kmol.
- Parameters:
-
ubar Output vector of speciar partial molar internal energies. Length = m_kk. units are J/kmol.
Reimplemented in IdealGasPhase, IdealSolnGasVPSS, and SingleSpeciesTP.
Definition at line 1244 of file ThermoPhase.h.
References ThermoPhase::err().
| void getPartialMolarVolumes | ( | doublereal * | vbar | ) | const [virtual] |
Return an array of partial molar volumes for the species in the mixture.
Units: m^3/kmol.
For this solution, the partial molar volumes are functions of the pressure derivatives of the activity coefficients.
![\[ \bar V_k(T,P) = V^{\triangle}_k(T,P) + R T \frac{d \ln(\gamma^{\triangle}_k) }{dP} \]](form_207.png)
![\[ \bar V_o(T,P) = V^o_o(T,P) + R T \frac{d \ln(a_o)}{dP} \]](form_208.png)
- Parameters:
-
vbar Output vector of speciar partial molar volumes. Length = m_kk. units are m^3/kmol.
Reimplemented from ThermoPhase.
Definition at line 1237 of file HMWSoln.cpp.
References Cantera::GasConstant, VPStandardStateTP::getStandardVolumes(), HMWSoln::m_dlnActCoeffMolaldP_Scaled, HMWSoln::s_update_dlnMolalityActCoeff_dP(), HMWSoln::s_update_lnMolalityActCoeff(), and State::temperature().
| void getPureGibbs | ( | doublereal * | gpure | ) | const [inline, virtual, inherited] |
Get the nondimensional Gibbs functions for the standard state of the species at the current T and P.
(Note resolved at this level)
- Parameters:
-
gpure Output vector of standard state Gibbs free energies. length = m_kk. units are J/kmol.
- Todo:
- This could be eliminated. It doesn't fit into the current naming convention.
Reimplemented from ThermoPhase.
Definition at line 251 of file VPStandardStateTP.cpp.
References VPSSMgr::getStandardChemPotentials(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
| void getReferenceComposition | ( | doublereal *const | x | ) | const [virtual, inherited] |
Gets the reference composition.
The reference mole fraction is a safe mole fraction.
- Parameters:
-
x Mole fraction vector containing the reference composition.
Definition at line 911 of file ThermoPhase.cpp.
References Phase::m_kk, and ThermoPhase::xMol_Ref.
| void getStandardChemPotentials | ( | doublereal * | mu | ) | const [virtual, inherited] |
Get the array of chemical potentials at unit activity.
These are the standard state chemical potentials 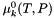 . The values are evaluated at the current temperature and pressure.
. The values are evaluated at the current temperature and pressure.
- Parameters:
-
mu Output vector of standard state chemical potentials. length = m_kk. units are J / kmol.
Reimplemented from ThermoPhase.
Definition at line 209 of file VPStandardStateTP.cpp.
References ThermoPhase::_RT(), VPStandardStateTP::getGibbs_RT(), and Phase::m_kk.
Referenced by IdealSolnGasVPSS::getChemPotentials(), IdealMolalSoln::getChemPotentials(), HMWSoln::getChemPotentials(), DebyeHuckel::getChemPotentials(), and MolalityVPSSTP::report().
| void getStandardVolumes | ( | doublereal * | vol | ) | const [virtual, inherited] |
Get the molar volumes of each species in their standard states at the current T and P of the solution.
units = m^3 / kmol
This is redefined here to call the internal function, _updateStandardStateThermo(), which calculates all standard state properties at the same time.
- Parameters:
-
vol Output vector of species volumes. length = m_kk. units = m^3 / kmol
Reimplemented from ThermoPhase.
Definition at line 266 of file VPStandardStateTP.cpp.
References VPSSMgr::getStandardVolumes(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
Referenced by IdealSolnGasVPSS::getPartialMolarVolumes(), IdealMolalSoln::getPartialMolarVolumes(), HMWSoln::getPartialMolarVolumes(), DebyeHuckel::getPartialMolarVolumes(), and HMWSoln::standardConcentration().
| void getStandardVolumes_ref | ( | doublereal * | vol | ) | const [virtual, inherited] |
Get the molar volumes of the species reference states at the current T and P_ref of the solution.
units = m^3 / kmol
- Parameters:
-
vol Output vector containing the standard state volumes. Length: m_kk.
Reimplemented from ThermoPhase.
Definition at line 341 of file VPStandardStateTP.cpp.
References VPSSMgr::getStandardVolumes_ref(), VPStandardStateTP::m_VPSS_ptr, and VPStandardStateTP::updateStandardStateThermo().
| void getUnitsStandardConc | ( | double * | uA, | |
| int | k = 0, |
|||
| int | sizeUA = 6 | |||
| ) | const [virtual] |
Returns the units of the standard and generalized concentrations.
Note they have the same units, as their ratio is defined to be equal to the activity of the kth species in the solution, which is unitless.
This routine is used in print out applications where the units are needed. Usually, MKS units are assumed throughout the program and in the XML input files.
The base ThermoPhase class assigns the default quantities of (kmol/m3) for all species. Inherited classes are responsible for overriding the default values if necessary.
- Parameters:
-
uA Output vector containing the units uA[0] = kmol units - default = 1 uA[1] = m units - default = -nDim(), the number of spatial dimensions in the Phase class. uA[2] = kg units - default = 0; uA[3] = Pa(pressure) units - default = 0; uA[4] = Temperature units - default = 0; uA[5] = time units - default = 0 k species index. Defaults to 0. sizeUA output int containing the size of the vector. Currently, this is equal to 6.
Reimplemented from MolalityVPSSTP.
Definition at line 986 of file HMWSoln.cpp.
References Phase::nDim().
| void getUnscaledMolalityActivityCoefficients | ( | doublereal * | acMolality | ) | const [virtual] |
Get the array of unscaled non-dimensional molality based activity coefficients at the current solution temperature, pressure, and solution concentration.
See Denbigh p. 278 for a thorough discussion. This class must be overwritten in classes which derive from MolalityVPSSTP. This function takes over from the molar-based activity coefficient calculation, getActivityCoefficients(), in derived classes.
- Parameters:
-
acMolality Output vector containing the molality based activity coefficients. length: m_kk.
Reimplemented from MolalityVPSSTP.
Definition at line 1040 of file HMWSoln.cpp.
References HMWSoln::A_Debye_TP(), HMWSoln::m_lnActCoeffMolal_Unscaled, HMWSoln::s_update_lnMolalityActCoeff(), and VPStandardStateTP::updateStandardStateThermo().
| doublereal gibbs_mass | ( | ) | const [inline, inherited] |
Specific Gibbs function.
Units: J/kg.
Definition at line 1503 of file ThermoPhase.h.
References ThermoPhase::gibbs_mole(), and State::meanMolecularWeight().
Referenced by ThermoPhase::report(), PureFluidPhase::report(), and MolalityVPSSTP::report().
| doublereal gibbs_mole | ( | ) | const [virtual] |
Molar Gibbs function. Units: J/kmol.
Reimplemented from ThermoPhase.
Definition at line 716 of file HMWSoln.cpp.
References DATA_PTR, HMWSoln::getPartialMolarEntropies(), HMWSoln::m_tmpV, and State::mean_X().
| doublereal Hf298SS | ( | const int | k | ) | const [inline, inherited] |
Report the 298 K Heat of Formation of the standard state of one species (J kmol-1).
The 298K Heat of Formation is defined as the enthalpy change to create the standard state of the species from its constituent elements in their standard states at 298 K and 1 bar.
- Parameters:
-
k species index
- Returns:
- Returns the current value of the Heat of Formation at 298K and 1 bar
Definition at line 816 of file ThermoPhase.h.
References ThermoPhase::err().
| std::string id | ( | ) | const [inherited] |
Return the string id for the phase.
Returns the id of the phase. The ID of the phase is set to the string name of the phase within the XML file Generally, it refers to the individual model name that denotes the species, the thermo, and the reaction rate info.
Definition at line 116 of file Phase.cpp.
References Phase::m_id.
Referenced by Kinetics::kineticsSpeciesIndex(), MultiPhase::phaseIndex(), and MultiPhase::phaseName().
| int index | ( | ) | const [inline, inherited] |
For internal use only.
Index number. This method can be used to identify the location of a phase object in a list, and is used by the interface library (clib) routines for this purpose.
Reimplemented from Phase.
Definition at line 1985 of file ThermoPhase.h.
References ThermoPhase::m_index.
| void init | ( | const array_fp & | mw | ) | [protected, inherited] |
For internal use only.
Initialize. Make a local copy of the vector of molecular weights, and resize the composition arrays to the appropriate size. The only information an instance of State has about the species is their molecular weights.
- Parameters:
-
mw Vector of molecular weights of the species.
Definition at line 244 of file State.cpp.
References Cantera::int2str(), State::m_kk, State::m_mmw, State::m_molwts, State::m_rmolwts, State::m_y, State::m_ym, and Cantera::Tiny.
Referenced by Phase::freezeSpecies().
| void initLengths | ( | ) | [private] |
Initialize all of the species - dependent lengths in the object.
Reimplemented from MolalityVPSSTP.
Definition at line 1648 of file HMWSoln.cpp.
References HMWSoln::counterIJ_setup(), HMWSoln::CROP_speciesCropped_, HMWSoln::IMS_lnActCoeffMolal_, HMWSoln::m_Aionic, HMWSoln::m_Alpha1MX_ij, HMWSoln::m_Alpha2MX_ij, HMWSoln::m_Beta0MX_ij, HMWSoln::m_Beta0MX_ij_coeff, HMWSoln::m_Beta0MX_ij_L, HMWSoln::m_Beta0MX_ij_LL, HMWSoln::m_Beta0MX_ij_P, HMWSoln::m_Beta1MX_ij, HMWSoln::m_Beta1MX_ij_coeff, HMWSoln::m_Beta1MX_ij_L, HMWSoln::m_Beta1MX_ij_LL, HMWSoln::m_Beta1MX_ij_P, HMWSoln::m_Beta2MX_ij, HMWSoln::m_Beta2MX_ij_coeff, HMWSoln::m_Beta2MX_ij_L, HMWSoln::m_Beta2MX_ij_LL, HMWSoln::m_Beta2MX_ij_P, HMWSoln::m_BMX_IJ, HMWSoln::m_BMX_IJ_L, HMWSoln::m_BMX_IJ_LL, HMWSoln::m_BMX_IJ_P, HMWSoln::m_BphiMX_IJ, HMWSoln::m_BphiMX_IJ_L, HMWSoln::m_BphiMX_IJ_LL, HMWSoln::m_BphiMX_IJ_P, HMWSoln::m_BprimeMX_IJ, HMWSoln::m_BprimeMX_IJ_L, HMWSoln::m_BprimeMX_IJ_LL, HMWSoln::m_BprimeMX_IJ_P, HMWSoln::m_CMX_IJ, HMWSoln::m_CMX_IJ_L, HMWSoln::m_CMX_IJ_LL, HMWSoln::m_CMX_IJ_P, HMWSoln::m_CounterIJ, HMWSoln::m_CphiMX_ij, HMWSoln::m_CphiMX_ij_coeff, HMWSoln::m_CphiMX_ij_L, HMWSoln::m_CphiMX_ij_LL, HMWSoln::m_CphiMX_ij_P, HMWSoln::m_d2lnActCoeffMolaldT2_Scaled, HMWSoln::m_d2lnActCoeffMolaldT2_Unscaled, HMWSoln::m_dlnActCoeffMolaldP_Scaled, HMWSoln::m_dlnActCoeffMolaldP_Unscaled, HMWSoln::m_dlnActCoeffMolaldT_Scaled, HMWSoln::m_dlnActCoeffMolaldT_Unscaled, HMWSoln::m_electrolyteSpeciesType, HMWSoln::m_expg0_RT, HMWSoln::m_formPitzerTemp, HMWSoln::m_g2func_IJ, HMWSoln::m_gamma_tmp, HMWSoln::m_gfunc_IJ, HMWSoln::m_h2func_IJ, HMWSoln::m_hfunc_IJ, HMWSoln::m_Lambda_nj, HMWSoln::m_Lambda_nj_coeff, HMWSoln::m_Lambda_nj_L, HMWSoln::m_Lambda_nj_LL, HMWSoln::m_Lambda_nj_P, HMWSoln::m_lnActCoeffMolal_Scaled, HMWSoln::m_lnActCoeffMolal_Unscaled, HMWSoln::m_molalitiesCropped, HMWSoln::m_Mu_nnn, HMWSoln::m_Mu_nnn_coeff, HMWSoln::m_Mu_nnn_L, HMWSoln::m_Mu_nnn_LL, HMWSoln::m_Mu_nnn_P, HMWSoln::m_pe, HMWSoln::m_Phi_IJ, HMWSoln::m_Phi_IJ_L, HMWSoln::m_Phi_IJ_LL, HMWSoln::m_Phi_IJ_P, HMWSoln::m_PhiPhi_IJ, HMWSoln::m_PhiPhi_IJ_L, HMWSoln::m_PhiPhi_IJ_LL, HMWSoln::m_PhiPhi_IJ_P, HMWSoln::m_Phiprime_IJ, HMWSoln::m_pp, HMWSoln::m_Psi_ijk, HMWSoln::m_Psi_ijk_coeff, HMWSoln::m_Psi_ijk_L, HMWSoln::m_Psi_ijk_LL, HMWSoln::m_Psi_ijk_P, HMWSoln::m_speciesCharge_Stoich, Constituents::m_speciesSize, HMWSoln::m_Theta_ij, HMWSoln::m_Theta_ij_coeff, HMWSoln::m_Theta_ij_L, HMWSoln::m_Theta_ij_LL, HMWSoln::m_Theta_ij_P, HMWSoln::m_tmpV, Constituents::nSpecies(), and Array2D::resize().
Referenced by HMWSoln::initThermo(), and HMWSoln::initThermoXML().
| void initThermo | ( | ) | [virtual] |
Internal initialization required after all species have been added.
For internal use only.
Initialize. This method is provided to allow subclasses to perform any initialization required after all species have been added. For example, it might be used to resize internal work arrays that must have an entry for each species. The base class implementation does nothing, and subclasses that do not require initialization do not need to overload this method. When importing a CTML phase description, this method is called just prior to returning from function importPhase.
- See also:
- importCTML.cpp
Reimplemented from MolalityVPSSTP.
Definition at line 1041 of file HMWSoln_input.cpp.
References HMWSoln::initLengths().
| void initThermoFile | ( | std::string | inputFile, | |
| std::string | id | |||
| ) | [virtual, inherited] |
For internal use only.
Initialization of a ThermoPhase object using an ctml file.
This routine is a precursor to initThermoXML(XML_Node*) routine, which does most of the work. Here we read extra information about the XML description of a phase. Regular information about elements and species and their reference state thermodynamic information have already been read at this point. For example, we do not need to call this function for ideal gas equations of state.
- Parameters:
-
inputFile XML file containing the description of the phase id Optional parameter identifying the name of the phase. If none is given, the first XML phase element encountered will be used.
Definition at line 830 of file ThermoPhase.cpp.
References XML_Node::build(), XML_Node::copy(), Cantera::findInputFile(), Cantera::findXMLPhase(), ThermoPhase::initThermoXML(), and Phase::xml().
| void initThermoXML | ( | XML_Node & | phaseNode, | |
| std::string | id | |||
| ) | [virtual] |
Initialize the phase parameters from an XML file.
Process the XML file after species are set up.
initThermoXML() (virtual from ThermoPhase)
This gets called from importPhase(). It processes the XML file after the species are set up. This is the main routine for reading in activity coefficient parameters.
- Parameters:
-
phaseNode This object must be the phase node of a complete XML tree description of the phase, including all of the species data. In other words while "phase" must point to an XML phase object, it must have sibling nodes "speciesData" that describe the species in the phase. id ID of the phase. If nonnull, a check is done to see if phaseNode is pointing to the phase with the correct id.
This gets called from importPhase(). It processes the XML file after the species are set up. This is the main routine for reading in activity coefficient parameters.
- Parameters:
-
phaseNode This object must be the phase node of a complete XML tree description of the phase, including all of the species data. In other words while "phase" must point to an XML phase object, it must have sibling nodes "speciesData" that describe the species in the phase. id ID of the phase. If nonnull, a check is done to see if phaseNode is pointing to the phase with the correct id.
Reimplemented from MolalityVPSSTP.
Definition at line 1265 of file HMWSoln_input.cpp.
References XML_Node::attrib(), HMWSoln::calcIMSCutoffParams_(), HMWSoln::calcMCCutoffParams_(), XML_Node::child(), PDSS::density(), XML_Node::findByAttr(), XML_Node::findByName(), Cantera::fpValue(), Cantera::get_XML_NameID(), ctml::getChildValue(), ctml::getFloat(), ctml::getMap(), ctml::getOptionalFloat(), ctml::getStringArray(), XML_Node::hasAttrib(), XML_Node::hasChild(), HMWSoln::IMS_typeCutoff_, HMWSoln::initLengths(), HMWSoln::interp_est(), Cantera::lowercase(), HMWSoln::m_A_Debye, HMWSoln::m_Aionic, HMWSoln::m_electrolyteSpeciesType, HMWSoln::m_form_A_Debye, MolalityVPSSTP::m_indexSolvent, Phase::m_kk, HMWSoln::m_maxIionicStrength, Constituents::m_speciesCharge, HMWSoln::m_speciesCharge_Stoich, Constituents::m_speciesSize, HMWSoln::m_waterProps, HMWSoln::m_waterSS, PDSS::molecularWeight(), XML_Node::name(), XML_Node::nChildren(), Cantera::OneAtm, HMWSoln::readXMLBinarySalt(), HMWSoln::readXMLCroppingCoefficients(), HMWSoln::readXMLLambdaNeutral(), HMWSoln::readXMLPsiCommonAnion(), HMWSoln::readXMLPsiCommonCation(), HMWSoln::readXMLThetaAnion(), HMWSoln::readXMLThetaCation(), HMWSoln::readXMLZetaCation(), XML_Node::root(), MolalityVPSSTP::setMoleFSolventMin(), MolalityVPSSTP::setSolvent(), PDSS::setState_TP(), ThermoPhase::speciesData(), Constituents::speciesIndex(), Constituents::speciesName(), Constituents::speciesNames(), and Cantera::toSI().
| doublereal intEnergy_mass | ( | ) | const [inline, inherited] |
Specific internal energy.
Units: J/kg.
Definition at line 1489 of file ThermoPhase.h.
References ThermoPhase::intEnergy_mole(), and State::meanMolecularWeight().
Referenced by ThermoPhase::report(), PureFluidPhase::report(), MolalityVPSSTP::report(), ThermoPhase::setState_HPorUV(), and SingleSpeciesTP::setState_UV().
| doublereal intEnergy_mole | ( | ) | const [virtual] |
Molar internal energy. Units: J/kmol.
Molar internal energy of the solution. Units: J/kmol. (HKM -> Bump up to Parent object)
Reimplemented from ThermoPhase.
Definition at line 697 of file HMWSoln.cpp.
References HMWSoln::enthalpy_mole(), State::molarDensity(), and HMWSoln::pressure().
| int interp_est | ( | std::string | estString | ) | [static, private] |
Utility function to assign an integer value from a string for the ElectrolyteSpeciesType field.
utility function to assign an integer value from a string for the ElectrolyteSpeciesType field.
- Parameters:
-
estString string name of the electrolyte species type
Definition at line 36 of file HMWSoln_input.cpp.
References Cantera::lowercase().
Referenced by HMWSoln::initThermoXML().
| doublereal isothermalCompressibility | ( | ) | const [virtual] |
The isothermal compressibility.
Units: 1/Pa. The isothermal compressibility is defined as
![\[ \kappa_T = -\frac{1}{v}\left(\frac{\partial v}{\partial P}\right)_T \]](form_95.png)
Reimplemented from ThermoPhase.
Definition at line 785 of file HMWSoln.cpp.
| doublereal logStandardConc | ( | int | k = 0 |
) | const [virtual] |
Returns the natural logarithm of the standard concentration of the kth species.
- Parameters:
-
k Species index
Reimplemented from MolalityVPSSTP.
Definition at line 959 of file HMWSoln.cpp.
| doublereal massFraction | ( | std::string | name | ) | const [inherited] |
Return the mass fraction of a single species.
- Parameters:
-
name String name of the species
- Returns:
- Mass Fraction of the species
Definition at line 328 of file Phase.cpp.
References State::massFractions(), and Constituents::speciesIndex().
| doublereal massFraction | ( | int | k | ) | const [inherited] |
| const doublereal* massFractions | ( | ) | const [inline, inherited] |
Returns a read-only pointer to the start of the massFraction array.
The pointer returned is readonly
- Returns:
- returns a pointer to a vector of doubles of length m_kk.
Definition at line 242 of file State.h.
References State::m_y.
Referenced by Phase::massFraction().
| doublereal maxTemp | ( | int | k = -1 |
) | const [inline, inherited] |
Maximum temperature for which the thermodynamic data for the species are valid.
If no argument is supplied, the value returned will be the highest temperature at which the data for all species are valid. Otherwise, the value will be only for species k. This function is a wrapper that calls the species thermo maxTemp function.
- Parameters:
-
k index of the species. Default is -1, which will return the min of the max value over all species.
Definition at line 845 of file ThermoPhase.h.
References ThermoPhase::m_spthermo, and SpeciesThermo::maxTemp().
Referenced by MultiPhase::addPhase(), ThermoPhase::setState_HPorUV(), and ThermoPhase::setState_SPorSV().
| doublereal mean_X | ( | const doublereal *const | Q | ) | const [inherited] |
Evaluate the mole-fraction-weighted mean of Q:
![\[ \sum_k X_k Q_k. \]](form_451.png)
Array Q should contain pure-species molar property values.
- Parameters:
-
Q input vector of length m_kk that is to be averaged.
- Returns:
- mole-freaction-weighted mean of Q
Definition at line 223 of file State.cpp.
References State::m_mmw, and State::m_ym.
Referenced by IdealSolnGasVPSS::cp_mole(), IdealSolidSolnPhase::cp_mole(), IdealMolalSoln::cp_mole(), IdealGasPhase::cp_mole(), DebyeHuckel::cp_mole(), LatticePhase::cv_mole(), HMWSoln::cv_mole(), ConstDensityThermo::cv_mole(), SurfPhase::enthalpy_mole(), IdealSolnGasVPSS::enthalpy_mole(), IdealSolidSolnPhase::enthalpy_mole(), IdealMolalSoln::enthalpy_mole(), IdealGasPhase::enthalpy_mole(), DebyeHuckel::enthalpy_mole(), IdealSolnGasVPSS::entropy_mole(), IdealSolidSolnPhase::entropy_mole(), IdealMolalSoln::entropy_mole(), IdealGasPhase::entropy_mole(), DebyeHuckel::entropy_mole(), IdealSolidSolnPhase::gibbs_mole(), IdealMolalSoln::gibbs_mole(), HMWSoln::gibbs_mole(), DebyeHuckel::gibbs_mole(), IdealSolidSolnPhase::intEnergy_mole(), IdealMolalSoln::intEnergy_mole(), IdealGasPhase::intEnergy_mole(), and HMWSoln::relative_enthalpy().
| doublereal mean_Y | ( | const doublereal *const | Q | ) | const [inherited] |
Evaluate the mass-fraction-weighted mean of Q:
![\[ \sum_k Y_k Q_k \]](form_452.png)
.
- Parameters:
-
Q Array Q contains a vector of species property values in mass units.
- Returns:
- Return value containing the mass-fraction-weighted mean of Q.
Definition at line 227 of file State.cpp.
References Cantera::dot(), and State::m_y.
| doublereal meanMolecularWeight | ( | ) | const [inline, inherited] |
The mean molecular weight.
Units: (kg/kmol)
Definition at line 282 of file State.h.
References State::m_mmw.
Referenced by IdealSolnGasVPSS::calcDensity(), IdealMolalSoln::calcDensity(), DebyeHuckel::calcDensity(), ThermoPhase::cp_mass(), ThermoPhase::cv_mass(), ThermoPhase::enthalpy_mass(), ThermoPhase::entropy_mass(), IdealSolidSolnPhase::getActivityConcentrations(), WaterSSTP::getStandardVolumes_ref(), ThermoPhase::gibbs_mass(), ThermoPhase::intEnergy_mass(), State::molarDensity(), ThermoPhase::report(), PureFluidPhase::report(), MolalityVPSSTP::report(), State::setMolarDensity(), and IdealGasPhase::setPressure().
| doublereal minTemp | ( | int | k = -1 |
) | const [inline, inherited] |
Minimum temperature for which the thermodynamic data for the species or phase are valid.
If no argument is supplied, the value returned will be the lowest temperature at which the data for all species are valid. Otherwise, the value will be only for species k. This function is a wrapper that calls the species thermo minTemp function.
- Parameters:
-
k index of the species. Default is -1, which will return the max of the min value over all species.
Definition at line 776 of file ThermoPhase.h.
References ThermoPhase::m_spthermo, and SpeciesThermo::minTemp().
Referenced by MultiPhase::addPhase(), ThermoPhase::setState_HPorUV(), and ThermoPhase::setState_SPorSV().
| virtual void modifyOneHf298SS | ( | const int | k, | |
| const doublereal | Hf298New | |||
| ) | [inline, virtual, inherited] |
Modify the value of the 298 K Heat of Formation of one species in the phase (J kmol-1).
The 298K heat of formation is defined as the enthalpy change to create the standard state of the species from its constituent elements in their standard states at 298 K and 1 bar.
- Parameters:
-
k Species k Hf298New Specify the new value of the Heat of Formation at 298K and 1 bar
Definition at line 828 of file ThermoPhase.h.
References ThermoPhase::err().
| doublereal molarDensity | ( | ) | const [inherited] |
Molar density (kmol/m^3).
Definition at line 192 of file State.cpp.
References State::density(), and State::meanMolecularWeight().
Referenced by IdealSolidSolnPhase::enthalpy_mole(), ConstDensityThermo::getChemPotentials(), StoichSubstanceSSTP::getEnthalpy_RT(), MineralEQ3::getEnthalpy_RT(), StoichSubstanceSSTP::getIntEnergy_RT(), MineralEQ3::getIntEnergy_RT(), StoichSubstanceSSTP::getIntEnergy_RT_ref(), MineralEQ3::getIntEnergy_RT_ref(), MetalSHEelectrons::getIntEnergy_RT_ref(), IdealGasPhase::getPartialMolarVolumes(), IdealGasPhase::getStandardVolumes(), IdealSolnGasVPSS::intEnergy_mole(), IdealSolidSolnPhase::intEnergy_mole(), HMWSoln::intEnergy_mole(), DebyeHuckel::intEnergy_mole(), ConstDensityThermo::logStandardConc(), IdealGasPhase::pressure(), IdealMolalSoln::setMolarDensity(), and DebyeHuckel::setMolarDensity().
| doublereal molarMass | ( | int | k | ) | const [inline, inherited] |
Return the Molar mass of species k.
Preferred name for molecular weight.
- Parameters:
-
k index for species
- Returns:
- Return the molar mass of species k kg/kmol.
Definition at line 240 of file Constituents.h.
References Constituents::molecularWeight().
| doublereal molecularWeight | ( | int | k | ) | const [inherited] |
Molecular weight of species k.
- Parameters:
-
k index of species k
- Returns:
- Returns the molecular weight of species
k.
Definition at line 240 of file Constituents.cpp.
References Constituents::m_weight, and Constituents::nSpecies().
Referenced by VPSSMgr_Water_HKFT::_updateRefStateThermo(), VPSSMgr_Water_ConstVol::_updateRefStateThermo(), VPSSMgr_Water_HKFT::_updateStandardStateThermo(), VPSSMgr_Water_ConstVol::_updateStandardStateThermo(), SingleSpeciesTP::cv_mole(), SingleSpeciesTP::getPartialMolarVolumes(), SingleSpeciesTP::getStandardVolumes(), VPSSMgr_Water_ConstVol::getStandardVolumes_ref(), PDSS::initThermo(), VPSSMgr_Water_HKFT::initThermoXML(), VPSSMgr_Water_ConstVol::initThermoXML(), PDSS_SSVol::initThermoXML(), PDSS_ConstVol::initThermoXML(), MineralEQ3::initThermoXML(), Constituents::molarMass(), and MolalityVPSSTP::setSolvent().
| const array_fp & molecularWeights | ( | ) | const [inherited] |
Return a const reference to the internal vector of molecular weights.
Reimplemented from Constituents.
Definition at line 298 of file Phase.cpp.
Referenced by Phase::getMolecularWeights().
| const doublereal * moleFractdivMMW | ( | ) | const [inherited] |
Returns a read-only pointer to the start of the moleFraction/MW array.
This array is the array of mole fractions, each divided by the mean molecular weight.
Definition at line 215 of file State.cpp.
References State::m_ym.
Referenced by IdealSolnGasVPSS::calcDensity(), IdealSolidSolnPhase::calcDensity(), and IdealSolidSolnPhase::getActivityConcentrations().
| doublereal moleFraction | ( | std::string | name | ) | const [inherited] |
Return the mole fraction of a single species.
- Parameters:
-
name String name of the species
- Returns:
- Mole fraction of the species
Definition at line 318 of file Phase.cpp.
References Phase::moleFraction(), and Constituents::speciesIndex().
| doublereal moleFraction | ( | int | k | ) | const [inherited] |
Return the mole fraction of a single species.
- Parameters:
-
k String name of the species
- Returns:
- Mole fraction of the species
Reimplemented from State.
Definition at line 314 of file Phase.cpp.
Referenced by Phase::chargeDensity(), IdealMolalSoln::getActivities(), HMWSoln::getActivities(), DebyeHuckel::getActivities(), MolalityVPSSTP::getActivityCoefficients(), IdealSolnGasVPSS::getActivityConcentrations(), IdealSolnGasVPSS::getChemPotentials(), IdealSolidSolnPhase::getChemPotentials(), IdealMolalSoln::getChemPotentials(), IdealGasPhase::getChemPotentials(), HMWSoln::getChemPotentials(), DebyeHuckel::getChemPotentials(), IdealSolidSolnPhase::getChemPotentials_RT(), IdealMolalSoln::getMolalityActivityCoefficients(), Phase::getMoleFractionsByName(), IdealSolnGasVPSS::getPartialMolarEntropies(), IdealSolidSolnPhase::getPartialMolarEntropies(), IdealMolalSoln::getPartialMolarEntropies(), IdealGasPhase::getPartialMolarEntropies(), HMWSoln::getPartialMolarEntropies(), DebyeHuckel::getPartialMolarEntropies(), Phase::moleFraction(), DebyeHuckel::s_update_d2lnMolalityActCoeff_dT2(), DebyeHuckel::s_update_dlnMolalityActCoeff_dP(), DebyeHuckel::s_update_dlnMolalityActCoeff_dT(), DebyeHuckel::s_update_lnMolalityActCoeff(), IdealMolalSoln::s_updateIMS_lnMolalityActCoeff(), HMWSoln::s_updateIMS_lnMolalityActCoeff(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
| doublereal moleFSolventMin | ( | ) | const [inherited] |
Returns the minimum mole fraction in the molality formulation.
Definition at line 200 of file MolalityVPSSTP.cpp.
References MolalityVPSSTP::m_xmolSolventMIN.
| std::string name | ( | ) | const [inherited] |
Return the name of the phase.
Returns the name of the phase. The name of the phase is set to the string name of the phase within the XML file Generally, it refers to the individual model name that denotes the species, the thermo, and the reaction rate info. It may also refer more specifically to a location within the domain.
Definition at line 124 of file Phase.cpp.
References Phase::m_name.
Referenced by Cantera::operator<<(), ThermoPhase::report(), PureFluidPhase::report(), MolalityVPSSTP::report(), and vcs_MultiPhaseEquil::reportCSV().
| doublereal nAtoms | ( | int | k, | |
| int | m | |||
| ) | const [inherited] |
Number of atoms of element m in species k.
- Parameters:
-
k species index m element index
Definition at line 463 of file Constituents.cpp.
References Constituents::m_Elements, Constituents::m_speciesComp, Constituents::nElements(), Elements::nElements(), and Constituents::nSpecies().
Referenced by PDSS_HKFT::convertDGFormation(), MolalityVPSSTP::findCLMIndex(), MultiPhase::init(), and IdealSolidSolnPhase::setToEquilState().
| int nDim | ( | ) | const [inline, inherited] |
Returns the number of spatial dimensions (1, 2, or 3).
Definition at line 475 of file Phase.h.
References Phase::m_ndim.
Referenced by Kinetics::addPhase(), ThermoPhase::getUnitsStandardConc(), MolalityVPSSTP::getUnitsStandardConc(), IdealSolnGasVPSS::getUnitsStandardConc(), IdealSolidSolnPhase::getUnitsStandardConc(), IdealMolalSoln::getUnitsStandardConc(), HMWSoln::getUnitsStandardConc(), and DebyeHuckel::getUnitsStandardConc().
| int nElements | ( | ) | const [inherited] |
Number of elements.
Definition at line 88 of file Constituents.cpp.
References Constituents::m_Elements, and Elements::nElements().
Referenced by MultiPhase::addPhase(), PDSS_HKFT::convertDGFormation(), MolalityVPSSTP::findCLMIndex(), ThermoPhase::getElementPotentials(), IdealSolidSolnPhase::initLengths(), IdealGasPhase::initThermo(), Constituents::nAtoms(), and ThermoPhase::setElementPotentials().
| int nSpecies | ( | ) | const [inline, inherited] |
Returns the number of species in the phase.
Definition at line 222 of file Constituents.h.
References Constituents::m_kk.
Referenced by MultiPhase::addPhase(), MultiPhase::calcElemAbundances(), Phase::chargeDensity(), vcs_MultiPhaseEquil::equilibrate_TP(), Phase::freezeSpecies(), ThermoPhase::getActivities(), Phase::getMoleFractionsByName(), MultiPhase::getMoles(), MultiPhase::init(), VPStandardStateTP::initLengths(), VPSSMgr::initLengths(), MolalityVPSSTP::initLengths(), IdealSolnGasVPSS::initLengths(), IdealSolidSolnPhase::initLengths(), IdealMolalSoln::initLengths(), HMWSoln::initLengths(), DebyeHuckel::initLengths(), StoichSubstanceSSTP::initThermo(), SingleSpeciesTP::initThermo(), Constituents::molecularWeight(), Constituents::nAtoms(), Kinetics::nTotalSpecies(), ThermoPhase::report(), PureFluidPhase::report(), MolalityVPSSTP::report(), vcs_MultiPhaseEquil::reportCSV(), Phase::restoreState(), Phase::saveState(), Kinetics::selectPhase(), SurfPhase::setCoveragesByName(), Phase::setMassFractionsByName(), MolalityVPSSTP::setMolalitiesByName(), Phase::setMoleFractionsByName(), MultiPhase::setMoles(), MultiPhase::setPhaseMoleFractions(), ThermoPhase::setState_TPX(), ThermoPhase::setState_TPY(), Constituents::speciesName(), and MultiPhase::uploadMoleFractionsFromPhases().
Asignment operator.
Assignment operator for the object. Constructed object will be a clone of this object, but will also own all of its data.
- Parameters:
-
right Object to be copied.
Definition at line 257 of file HMWSoln.cpp.
References HMWSoln::CROP_ln_gamma_k_max, HMWSoln::CROP_ln_gamma_k_min, HMWSoln::CROP_ln_gamma_o_max, HMWSoln::CROP_ln_gamma_o_min, HMWSoln::CROP_speciesCropped_, HMWSoln::IMS_afCut_, HMWSoln::IMS_agCut_, HMWSoln::IMS_bfCut_, HMWSoln::IMS_bgCut_, HMWSoln::IMS_cCut_, HMWSoln::IMS_dfCut_, HMWSoln::IMS_dgCut_, HMWSoln::IMS_efCut_, HMWSoln::IMS_egCut_, HMWSoln::IMS_gamma_k_min_, HMWSoln::IMS_gamma_o_min_, HMWSoln::IMS_lnActCoeffMolal_, HMWSoln::IMS_slopefCut_, HMWSoln::IMS_slopegCut_, HMWSoln::IMS_typeCutoff_, HMWSoln::IMS_X_o_cutoff_, HMWSoln::m_A_Debye, HMWSoln::m_Aionic, HMWSoln::m_Alpha1MX_ij, HMWSoln::m_Alpha2MX_ij, HMWSoln::m_Beta0MX_ij, HMWSoln::m_Beta0MX_ij_coeff, HMWSoln::m_Beta0MX_ij_L, HMWSoln::m_Beta0MX_ij_LL, HMWSoln::m_Beta0MX_ij_P, HMWSoln::m_Beta1MX_ij, HMWSoln::m_Beta1MX_ij_coeff, HMWSoln::m_Beta1MX_ij_L, HMWSoln::m_Beta1MX_ij_LL, HMWSoln::m_Beta1MX_ij_P, HMWSoln::m_Beta2MX_ij, HMWSoln::m_Beta2MX_ij_coeff, HMWSoln::m_Beta2MX_ij_L, HMWSoln::m_Beta2MX_ij_LL, HMWSoln::m_Beta2MX_ij_P, HMWSoln::m_BMX_IJ, HMWSoln::m_BMX_IJ_L, HMWSoln::m_BMX_IJ_LL, HMWSoln::m_BMX_IJ_P, HMWSoln::m_BphiMX_IJ, HMWSoln::m_BphiMX_IJ_L, HMWSoln::m_BphiMX_IJ_LL, HMWSoln::m_BphiMX_IJ_P, HMWSoln::m_BprimeMX_IJ, HMWSoln::m_BprimeMX_IJ_L, HMWSoln::m_BprimeMX_IJ_LL, HMWSoln::m_BprimeMX_IJ_P, HMWSoln::m_CMX_IJ, HMWSoln::m_CMX_IJ_L, HMWSoln::m_CMX_IJ_LL, HMWSoln::m_CMX_IJ_P, HMWSoln::m_CounterIJ, HMWSoln::m_CphiMX_ij, HMWSoln::m_CphiMX_ij_coeff, HMWSoln::m_CphiMX_ij_L, HMWSoln::m_CphiMX_ij_LL, HMWSoln::m_CphiMX_ij_P, HMWSoln::m_d2lnActCoeffMolaldT2_Scaled, HMWSoln::m_d2lnActCoeffMolaldT2_Unscaled, HMWSoln::m_debugCalc, HMWSoln::m_densWaterSS, HMWSoln::m_dlnActCoeffMolaldP_Scaled, HMWSoln::m_dlnActCoeffMolaldP_Unscaled, HMWSoln::m_dlnActCoeffMolaldT_Scaled, HMWSoln::m_dlnActCoeffMolaldT_Unscaled, HMWSoln::m_expg0_RT, HMWSoln::m_form_A_Debye, HMWSoln::m_formGC, HMWSoln::m_formPitzer, HMWSoln::m_formPitzerTemp, HMWSoln::m_g2func_IJ, HMWSoln::m_gamma_tmp, HMWSoln::m_gfunc_IJ, HMWSoln::m_h2func_IJ, HMWSoln::m_hfunc_IJ, HMWSoln::m_IionicMolality, HMWSoln::m_IionicMolalityStoich, HMWSoln::m_Lambda_nj, HMWSoln::m_Lambda_nj_coeff, HMWSoln::m_Lambda_nj_L, HMWSoln::m_Lambda_nj_LL, HMWSoln::m_Lambda_nj_P, HMWSoln::m_lnActCoeffMolal_Scaled, HMWSoln::m_lnActCoeffMolal_Unscaled, HMWSoln::m_maxIionicStrength, HMWSoln::m_molalitiesAreCropped, HMWSoln::m_molalitiesCropped, HMWSoln::m_pe, HMWSoln::m_Phi_IJ, HMWSoln::m_Phi_IJ_L, HMWSoln::m_Phi_IJ_LL, HMWSoln::m_Phi_IJ_P, HMWSoln::m_PhiPhi_IJ, HMWSoln::m_PhiPhi_IJ_L, HMWSoln::m_PhiPhi_IJ_LL, HMWSoln::m_PhiPhi_IJ_P, HMWSoln::m_Phiprime_IJ, HMWSoln::m_pp, HMWSoln::m_Psi_ijk, HMWSoln::m_Psi_ijk_coeff, HMWSoln::m_Psi_ijk_L, HMWSoln::m_Psi_ijk_LL, HMWSoln::m_Psi_ijk_P, HMWSoln::m_speciesCharge_Stoich, HMWSoln::m_TempPitzerRef, HMWSoln::m_Theta_ij, HMWSoln::m_Theta_ij_coeff, HMWSoln::m_Theta_ij_L, HMWSoln::m_Theta_ij_LL, HMWSoln::m_Theta_ij_P, HMWSoln::m_tmpV, HMWSoln::m_waterProps, HMWSoln::m_waterSS, HMWSoln::MC_apCut_, HMWSoln::MC_bpCut_, HMWSoln::MC_cpCut_, HMWSoln::MC_dpCut_, HMWSoln::MC_epCut_, HMWSoln::MC_slopepCut_, HMWSoln::MC_X_o_cutoff_, and HMWSoln::MC_X_o_min_.
| doublereal osmoticCoefficient | ( | ) | const [virtual, inherited] |
Calculate the osmotic coefficient.
![\[ \phi = \frac{- ln(a_o)}{\tilde{M}_o \sum_{i \ne o} m_i} \]](form_363.png)
Note there are a few of definitions of the osmotic coefficient floating around. We use the one defined in (Activity Coefficients in Electrolyte Solutions, K. S. Pitzer CRC Press, Boca Raton, 1991, p. 85, Eqn. 28). This definition is most clearly related to theoretical calculation.
units = dimensionless
Definition at line 508 of file MolalityVPSSTP.cpp.
References DATA_PTR, Cantera::fmaxx(), MolalityVPSSTP::getActivities(), MolalityVPSSTP::m_indexSolvent, Phase::m_kk, MolalityVPSSTP::m_Mnaught, and MolalityVPSSTP::m_molalities.
| int pHScale | ( | ) | const [inherited] |
Reports the pH scale, which determines the scale for single-ion activity coefficients.
Single ion activity coefficients are not unique in terms of the representing actual measureable quantities.
- Returns:
- Return the pHscale type
Definition at line 153 of file MolalityVPSSTP.cpp.
References MolalityVPSSTP::m_pHScalingType.
| doublereal pressure | ( | ) | const [virtual] |
In this equation of state implementation, the density is a function only of the mole fractions.
Pressure.
Therefore, it can't be an independent variable. Instead, the pressure is used as the independent variable. Functions which try to set the thermodynamic state by calling setDensity() may cause an exception to be thrown. Pressure. Units: Pa. For this incompressible system, we return the internally storred independent value of the pressure.
Units: Pa. For this incompressible system, we return the internally storred independent value of the pressure.
Reimplemented from VPStandardStateTP.
Definition at line 749 of file HMWSoln.cpp.
References VPStandardStateTP::m_Pcurrent.
Referenced by HMWSoln::A_Debye_TP(), HMWSoln::d2A_DebyedT2_TP(), HMWSoln::dA_DebyedP_TP(), HMWSoln::dA_DebyedT_TP(), HMWSoln::intEnergy_mole(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), and HMWSoln::satPressure().
| void printCoeffs | ( | ) | const |
Print out all of the input coefficients.
This routine prints out the input pitzer coefficients for the current mechanism.
Definition at line 6289 of file HMWSoln.cpp.
Referenced by HMWSoln::HMWSoln().
| VPSSMgr * provideVPSSMgr | ( | ) | [inherited] |
Return a pointer to the VPSSMgr for this phase.
- Returns:
- Returns a pointer to the VPSSMgr for this phase
Definition at line 474 of file VPStandardStateTP.cpp.
References VPStandardStateTP::m_VPSS_ptr.
Referenced by PDSS::initThermo(), and PDSS::PDSS().
| void readXMLBinarySalt | ( | XML_Node & | BinSalt | ) | [private] |
Process an XML node called "binarySaltParameters".
This node contains all of the parameters necessary to describe the Pitzer model for that particular binary salt. This function reads the XML file and writes the coefficients it finds to an internal data structures.
- Parameters:
-
BinSalt reference to the XML_Node named binarySaltParameters containing the anion - cation interaction
Definition at line 67 of file HMWSoln_input.cpp.
References Cantera::atofCheck(), XML_Node::attrib(), Constituents::charge(), XML_Node::child(), DATA_PTR, ctml::getFloatArray(), Cantera::lowercase(), HMWSoln::m_Alpha1MX_ij, HMWSoln::m_Alpha2MX_ij, HMWSoln::m_Beta0MX_ij, HMWSoln::m_Beta0MX_ij_coeff, HMWSoln::m_Beta1MX_ij, HMWSoln::m_Beta1MX_ij_coeff, HMWSoln::m_Beta2MX_ij, HMWSoln::m_Beta2MX_ij_coeff, HMWSoln::m_CounterIJ, HMWSoln::m_CphiMX_ij, HMWSoln::m_CphiMX_ij_coeff, HMWSoln::m_formPitzerTemp, Phase::m_kk, Constituents::m_speciesCharge, XML_Node::name(), XML_Node::nChildren(), Constituents::speciesIndex(), Constituents::speciesName(), and XML_Node::value().
Referenced by HMWSoln::initThermoXML().
| void readXMLCroppingCoefficients | ( | const XML_Node & | acNode | ) | [private] |
Process an XML node called "croppingCoefficients" for the cropping coefficients values.
- Parameters:
-
acNode Activity Coefficient XML Node
Definition at line 1010 of file HMWSoln_input.cpp.
References XML_Node::child(), HMWSoln::CROP_ln_gamma_k_max, HMWSoln::CROP_ln_gamma_k_min, HMWSoln::CROP_ln_gamma_o_max, HMWSoln::CROP_ln_gamma_o_min, ctml::getOptionalFloat(), and XML_Node::hasChild().
Referenced by HMWSoln::initThermoXML().
| void readXMLLambdaNeutral | ( | XML_Node & | BinSalt | ) | [private] |
Process an XML node called "lambdaNeutral".
Process an XML node called "LambdaNeutral".
This node contains all of the parameters necessary to describe the binary interactions between one neutral species and any other species (neutral or otherwise) in the mechanism.
- Parameters:
-
BinSalt reference to the XML_Node named lambdaNeutral containing multiple Neutral - species interactions
This node contains all of the parameters necessary to describe the binary interactions between one neutral species and any other species (neutral or otherwise) in the mechanism.
Definition at line 743 of file HMWSoln_input.cpp.
References XML_Node::attrib(), Constituents::charge(), XML_Node::child(), DATA_PTR, ctml::getFloatArray(), Cantera::lowercase(), HMWSoln::m_formPitzerTemp, Phase::m_kk, HMWSoln::m_Lambda_nj, HMWSoln::m_Lambda_nj_coeff, Constituents::m_speciesCharge, XML_Node::name(), XML_Node::nChildren(), Array2D::resize(), and Constituents::speciesIndex().
Referenced by HMWSoln::initThermoXML().
| void readXMLMunnnNeutral | ( | XML_Node & | BinSalt | ) | [private] |
Process an XML node called "MunnnNeutral".
This node contains all of the parameters necessary to describe the self-ternary interactions for one neutral species.
- Parameters:
-
BinSalt reference to the XML_Node named Munnn containing the self-ternary interaction
This node contains all of the parameters necessary to describe the self-ternary interactions for one neutral species.
Definition at line 829 of file HMWSoln_input.cpp.
References XML_Node::attrib(), Constituents::charge(), XML_Node::child(), DATA_PTR, ctml::getFloatArray(), Cantera::lowercase(), HMWSoln::m_formPitzerTemp, HMWSoln::m_Mu_nnn, HMWSoln::m_Mu_nnn_coeff, Constituents::m_speciesCharge, XML_Node::name(), XML_Node::nChildren(), and Constituents::speciesIndex().
| void readXMLPsiCommonAnion | ( | XML_Node & | BinSalt | ) | [private] |
Process an XML node called "psiCommonAnion".
Process an XML node called "PsiCommonAnion".
This node contains all of the parameters necessary to describe the ternary interactions between one anion and two cations.
- Parameters:
-
BinSalt reference to the XML_Node named psiCommonAnion containing the anion - cation1 - cation2 interaction
This node contains all of the parameters necessary to describe the binary interactions between two cations and one common anion.
Definition at line 593 of file HMWSoln_input.cpp.
References Cantera::atofCheck(), XML_Node::attrib(), Constituents::charge(), XML_Node::child(), DATA_PTR, ctml::getFloatArray(), Cantera::lowercase(), HMWSoln::m_CounterIJ, HMWSoln::m_formPitzerTemp, Phase::m_kk, HMWSoln::m_Psi_ijk, HMWSoln::m_Psi_ijk_coeff, Constituents::m_speciesCharge, HMWSoln::m_Theta_ij, XML_Node::name(), XML_Node::nChildren(), Constituents::speciesIndex(), and XML_Node::value().
Referenced by HMWSoln::initThermoXML().
| void readXMLPsiCommonCation | ( | XML_Node & | BinSalt | ) | [private] |
Process an XML node called "psiCommonCation".
This node contains all of the parameters necessary to describe the ternary interactions between one cation and two anions.
- Parameters:
-
BinSalt reference to the XML_Node named psiCommonCation containing the cation - anion1 - anion2 interaction
Definition at line 447 of file HMWSoln_input.cpp.
References Cantera::atofCheck(), XML_Node::attrib(), Constituents::charge(), XML_Node::child(), DATA_PTR, ctml::getFloatArray(), Cantera::lowercase(), HMWSoln::m_CounterIJ, HMWSoln::m_formPitzerTemp, Phase::m_kk, HMWSoln::m_Psi_ijk, HMWSoln::m_Psi_ijk_coeff, Constituents::m_speciesCharge, HMWSoln::m_Theta_ij, XML_Node::name(), XML_Node::nChildren(), Constituents::speciesIndex(), and XML_Node::value().
Referenced by HMWSoln::initThermoXML().
| void readXMLThetaAnion | ( | XML_Node & | BinSalt | ) | [private] |
Process an XML node called "thetaAnion".
This node contains all of the parameters necessary to describe the binary interactions between two anions.
- Parameters:
-
BinSalt reference to the XML_Node named thetaAnion containing the anion - anion interaction
This node contains all of the parameters necessary to describe the binary interactions between two anions.
Definition at line 273 of file HMWSoln_input.cpp.
References XML_Node::attrib(), Constituents::charge(), XML_Node::child(), DATA_PTR, ctml::getFloatArray(), Cantera::lowercase(), HMWSoln::m_CounterIJ, HMWSoln::m_formPitzerTemp, Phase::m_kk, Constituents::m_speciesCharge, HMWSoln::m_Theta_ij, HMWSoln::m_Theta_ij_coeff, XML_Node::name(), XML_Node::nChildren(), and Constituents::speciesIndex().
Referenced by HMWSoln::initThermoXML().
| void readXMLThetaCation | ( | XML_Node & | BinSalt | ) | [private] |
Process an XML node called "thetaCation".
This node contains all of the parameters necessary to describe the binary interactions between two cations.
- Parameters:
-
BinSalt reference to the XML_Node named thetaCation containing the cation - cation interaction
This node contains all of the parameters necessary to describe the binary interactions between two cation.
Definition at line 360 of file HMWSoln_input.cpp.
References XML_Node::attrib(), Constituents::charge(), XML_Node::child(), DATA_PTR, ctml::getFloatArray(), Cantera::lowercase(), HMWSoln::m_CounterIJ, HMWSoln::m_formPitzerTemp, Phase::m_kk, Constituents::m_speciesCharge, HMWSoln::m_Theta_ij, HMWSoln::m_Theta_ij_coeff, XML_Node::name(), XML_Node::nChildren(), and Constituents::speciesIndex().
Referenced by HMWSoln::initThermoXML().
| void readXMLZetaCation | ( | const XML_Node & | BinSalt | ) | [private] |
Process an XML node called "zetaCation".
This node contains all of the parameters necessary to describe the ternary interactions between one neutral, one cation, and one anion.
- Parameters:
-
BinSalt reference to the XML_Node named psiCommonCation containing the neutral - cation - anion interaction
Definition at line 905 of file HMWSoln_input.cpp.
References XML_Node::attrib(), Constituents::charge(), XML_Node::child(), DATA_PTR, ctml::getFloatArray(), Cantera::lowercase(), HMWSoln::m_formPitzerTemp, Phase::m_kk, HMWSoln::m_Psi_ijk, HMWSoln::m_Psi_ijk_coeff, Constituents::m_speciesCharge, XML_Node::name(), XML_Node::nChildren(), and Constituents::speciesIndex().
Referenced by HMWSoln::initThermoXML().
| bool ready | ( | ) | const [virtual, inherited] |
True if both elements and species have been frozen.
Reimplemented from Constituents.
Definition at line 363 of file Phase.cpp.
References Phase::m_kk, State::ready(), and Constituents::ready().
| doublereal refPressure | ( | ) | const [inline, inherited] |
Returns the reference pressure in Pa.
This function is a wrapper that calls the species thermo refPressure function.
Definition at line 759 of file ThermoPhase.h.
References ThermoPhase::m_spthermo, and SpeciesThermo::refPressure().
Referenced by IdealSolidSolnPhase::initLengths(), StoichSubstanceSSTP::initThermo(), SingleSpeciesTP::initThermo(), and IdealGasPhase::initThermo().
| doublereal relative_enthalpy | ( | ) | const [virtual] |
Excess molar enthalpy of the solution from the mixing process.
Units: J/ kmol.
Note this is kmol of the total solution.
Definition at line 634 of file HMWSoln.cpp.
References DATA_PTR, State::getMoleFractions(), HMWSoln::getPartialMolarEnthalpies(), HMWSoln::m_pp, HMWSoln::m_tmpV, and State::mean_X().
| doublereal relative_molal_enthalpy | ( | ) | const [virtual] |
Excess molar enthalpy of the solution from the mixing process on a molality basis.
Units: J/ (kmol add salt).
Note this is kmol of the guessed at salt composition
Definition at line 648 of file HMWSoln.cpp.
| std::string report | ( | bool | show_thermo = true |
) | const [virtual, inherited] |
returns a summary of the state of the phase as a string
Format a summary of the mixture state for output.
- Parameters:
-
show_thermo If true, extra information is printed out about the thermodynamic state of the system.
Reimplemented from ThermoPhase.
Definition at line 788 of file MolalityVPSSTP.cpp.
References ThermoPhase::cp_mass(), ThermoPhase::cp_mole(), ThermoPhase::cv_mass(), ThermoPhase::cv_mole(), State::density(), ThermoPhase::electricPotential(), ThermoPhase::enthalpy_mass(), ThermoPhase::enthalpy_mole(), ThermoPhase::entropy_mass(), ThermoPhase::entropy_mole(), MolalityVPSSTP::getActivities(), ThermoPhase::getChemPotentials(), MolalityVPSSTP::getMolalities(), MolalityVPSSTP::getMolalityActivityCoefficients(), State::getMoleFractions(), VPStandardStateTP::getStandardChemPotentials(), ThermoPhase::gibbs_mass(), ThermoPhase::gibbs_mole(), ThermoPhase::intEnergy_mass(), ThermoPhase::intEnergy_mole(), State::meanMolecularWeight(), Phase::name(), Constituents::nSpecies(), VPStandardStateTP::pressure(), Cantera::SmallNumber, Constituents::speciesIndex(), Constituents::speciesName(), and State::temperature().
| void restoreState | ( | int | lenstate, | |
| const doublereal * | state | |||
| ) | [inherited] |
Restore the state of the phase from a previously saved state vector.
- Parameters:
-
lenstate Length of the state vector state Vector of state conditions.
Definition at line 154 of file Phase.cpp.
References Constituents::nSpecies(), State::setDensity(), State::setMassFractions_NoNorm(), and State::setTemperature().
| void restoreState | ( | const vector_fp & | state | ) | [inherited] |
| doublereal s_NBS_CLM_d2lnMolalityActCoeff_dT2 | ( | ) | const [private] |
Calculate the second temperature derivative of the Chlorine activity coefficient on the NBS scale.
We assume here that the m_IionicMolality variable is up to date.
Definition at line 6473 of file HMWSoln.cpp.
Referenced by HMWSoln::s_updateScaling_pHScaling_dT2().
| doublereal s_NBS_CLM_dlnMolalityActCoeff_dP | ( | ) | const [private] |
Calculate the pressure derivative of the Chlorine activity coefficient.
We assume here that the m_IionicMolality variable is up to date.
Definition at line 6484 of file HMWSoln.cpp.
| doublereal s_NBS_CLM_dlnMolalityActCoeff_dT | ( | ) | const [private] |
Calculate the temperature derivative of the Chlorine activity coefficient on the NBS scale.
We assume here that the m_IionicMolality variable is up to date.
Definition at line 6462 of file HMWSoln.cpp.
Referenced by HMWSoln::s_updateScaling_pHScaling_dT().
| doublereal s_NBS_CLM_lnMolalityActCoeff | ( | ) | const [private] |
Calculate the Chlorine activity coefficient on the NBS scale.
We assume here that the m_IionicMolality variable is up to date.
Definition at line 6451 of file HMWSoln.cpp.
Referenced by HMWSoln::applyphScale(), and HMWSoln::s_updateScaling_pHScaling().
| void s_update_d2lnMolalityActCoeff_dT2 | ( | ) | const [private] |
This function calculates the temperature second derivative of the natural logarithm of the molality activity coefficients.
Definition at line 4280 of file HMWSoln.cpp.
Referenced by HMWSoln::getPartialMolarCp().
| void s_update_dlnMolalityActCoeff_dP | ( | ) | const [private] |
This function calculates the pressure derivative of the natural logarithm of the molality activity coefficients.
Definition at line 5173 of file HMWSoln.cpp.
References HMWSoln::CROP_speciesCropped_, DATA_PTR, Cantera::fbo_zero_dbl_1(), HMWSoln::m_dlnActCoeffMolaldP_Unscaled, HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), and HMWSoln::s_updateScaling_pHScaling_dP().
Referenced by HMWSoln::getPartialMolarVolumes().
| void s_update_dlnMolalityActCoeff_dT | ( | ) | const [private] |
This function calculates the temperature derivative of the.
s_update_dlnMolalityActCoeff_dT() (private, const )
natural logarithm of the molality activity coefficients.
This is the private function. It does all of the direct work.
Using internally stored values, this function calculates the temperature derivative of the logarithm of the activity coefficient for all species in the mechanism.
We assume that the activity coefficients are current.
solvent activity coefficient is on the molality scale. It's derivative is too.
Definition at line 3413 of file HMWSoln.cpp.
References HMWSoln::CROP_speciesCropped_, DATA_PTR, Cantera::fbo_zero_dbl_1(), HMWSoln::m_dlnActCoeffMolaldT_Unscaled, HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updateScaling_pHScaling_dT().
Referenced by HMWSoln::getPartialMolarCp(), HMWSoln::getPartialMolarEnthalpies(), and HMWSoln::getPartialMolarEntropies().
| void s_update_lnMolalityActCoeff | ( | ) | const [private] |
Calcuate the natural log of the molality-based activity coefficients.
Definition at line 1786 of file HMWSoln.cpp.
Referenced by HMWSoln::getActivities(), HMWSoln::getChemPotentials(), HMWSoln::getPartialMolarCp(), HMWSoln::getPartialMolarEnthalpies(), HMWSoln::getPartialMolarEntropies(), HMWSoln::getPartialMolarVolumes(), and HMWSoln::getUnscaledMolalityActivityCoefficients().
| void s_updateIMS_lnMolalityActCoeff | ( | ) | const [private] |
This function will be called to update the internally storred natural logarithm of the molality activity coefficients.
Definition at line 6173 of file HMWSoln.cpp.
References MolalityVPSSTP::calcMolalities(), HMWSoln::IMS_afCut_, HMWSoln::IMS_agCut_, HMWSoln::IMS_bfCut_, HMWSoln::IMS_bgCut_, HMWSoln::IMS_cCut_, HMWSoln::IMS_dfCut_, HMWSoln::IMS_dgCut_, HMWSoln::IMS_efCut_, HMWSoln::IMS_egCut_, HMWSoln::IMS_gamma_k_min_, HMWSoln::IMS_gamma_o_min_, HMWSoln::IMS_lnActCoeffMolal_, HMWSoln::IMS_typeCutoff_, HMWSoln::IMS_X_o_cutoff_, MolalityVPSSTP::m_indexSolvent, MolalityVPSSTP::m_xmolSolventMIN, MAX, and Phase::moleFraction().
| void s_updatePitzer_CoeffWRTemp | ( | int | doDerivs = 2 |
) | const [private] |
Calculates the Pitzer coefficients' dependence on the temperature.
It will also calculate the temperature derivatives of the coefficients, as they are important in the calculation of the latent heats and the heat capacities of the mixtures.
- Parameters:
-
doDerivs If >= 1, then the routine will calculate the first derivative. If >= 2, the routine will calculate the first and second temperature derivative. default = 2
Definition at line 2085 of file HMWSoln.cpp.
References HMWSoln::m_Beta0MX_ij, HMWSoln::m_Beta0MX_ij_coeff, HMWSoln::m_Beta0MX_ij_L, HMWSoln::m_Beta0MX_ij_LL, HMWSoln::m_Beta1MX_ij, HMWSoln::m_Beta1MX_ij_coeff, HMWSoln::m_Beta1MX_ij_L, HMWSoln::m_Beta1MX_ij_LL, HMWSoln::m_Beta2MX_ij, HMWSoln::m_Beta2MX_ij_coeff, HMWSoln::m_Beta2MX_ij_L, HMWSoln::m_Beta2MX_ij_LL, HMWSoln::m_CounterIJ, HMWSoln::m_CphiMX_ij, HMWSoln::m_CphiMX_ij_coeff, HMWSoln::m_CphiMX_ij_L, HMWSoln::m_CphiMX_ij_LL, HMWSoln::m_formPitzerTemp, HMWSoln::m_Lambda_nj, HMWSoln::m_Lambda_nj_coeff, HMWSoln::m_Lambda_nj_L, HMWSoln::m_Lambda_nj_LL, HMWSoln::m_Mu_nnn, HMWSoln::m_Mu_nnn_coeff, HMWSoln::m_Mu_nnn_L, HMWSoln::m_Mu_nnn_LL, HMWSoln::m_Psi_ijk, HMWSoln::m_Psi_ijk_coeff, HMWSoln::m_Psi_ijk_L, HMWSoln::m_Psi_ijk_LL, Constituents::m_speciesCharge, HMWSoln::m_TempPitzerRef, HMWSoln::m_Theta_ij, HMWSoln::m_Theta_ij_coeff, HMWSoln::m_Theta_ij_L, HMWSoln::m_Theta_ij_LL, Array2D::ptrColumn(), and State::temperature().
| void s_updatePitzer_d2lnMolalityActCoeff_dT2 | ( | ) | const [private] |
This function calculates the temperature second derivative of the natural logarithm of the molality activity coefficients.
Definition at line 4331 of file HMWSoln.cpp.
References HMWSoln::calc_lambdas(), HMWSoln::calc_thetas(), HMWSoln::counterIJ_setup(), HMWSoln::d2A_DebyedT2_TP(), DATA_PTR, HMWSoln::m_Alpha1MX_ij, HMWSoln::m_Alpha2MX_ij, HMWSoln::m_Beta0MX_ij_LL, HMWSoln::m_Beta1MX_ij_LL, HMWSoln::m_Beta2MX_ij_LL, HMWSoln::m_BMX_IJ_LL, HMWSoln::m_BphiMX_IJ_LL, HMWSoln::m_BprimeMX_IJ_LL, HMWSoln::m_CMX_IJ_LL, HMWSoln::m_CounterIJ, HMWSoln::m_CphiMX_ij_LL, HMWSoln::m_d2lnActCoeffMolaldT2_Unscaled, HMWSoln::m_debugCalc, HMWSoln::m_g2func_IJ, HMWSoln::m_gfunc_IJ, HMWSoln::m_h2func_IJ, HMWSoln::m_hfunc_IJ, HMWSoln::m_IionicMolality, MolalityVPSSTP::m_indexSolvent, HMWSoln::m_Lambda_nj_LL, HMWSoln::m_molalitiesCropped, HMWSoln::m_Mu_nnn_LL, HMWSoln::m_Phi_IJ_LL, HMWSoln::m_PhiPhi_IJ_LL, HMWSoln::m_Phiprime_IJ, HMWSoln::m_Psi_ijk_LL, Constituents::m_speciesCharge, HMWSoln::m_Theta_ij_LL, MolalityVPSSTP::m_weightSolvent, and Constituents::speciesName().
| void s_updatePitzer_dlnMolalityActCoeff_dP | ( | ) | const [private] |
Calculates the Pressure derivative of the natural logarithm of the molality activity coefficients.
Public function makes sure that all dependent data is up to date, before calling a private function
Definition at line 5212 of file HMWSoln.cpp.
References HMWSoln::calc_lambdas(), HMWSoln::calc_thetas(), HMWSoln::counterIJ_setup(), HMWSoln::dA_DebyedP_TP(), DATA_PTR, HMWSoln::m_A_Debye, HMWSoln::m_Alpha1MX_ij, HMWSoln::m_Alpha2MX_ij, HMWSoln::m_Beta0MX_ij_P, HMWSoln::m_Beta1MX_ij_P, HMWSoln::m_Beta2MX_ij_P, HMWSoln::m_BMX_IJ_P, HMWSoln::m_BphiMX_IJ_P, HMWSoln::m_BprimeMX_IJ_P, HMWSoln::m_CMX_IJ_P, HMWSoln::m_CounterIJ, HMWSoln::m_CphiMX_ij_P, HMWSoln::m_debugCalc, HMWSoln::m_dlnActCoeffMolaldP_Unscaled, HMWSoln::m_g2func_IJ, HMWSoln::m_gfunc_IJ, HMWSoln::m_h2func_IJ, HMWSoln::m_hfunc_IJ, HMWSoln::m_IionicMolality, MolalityVPSSTP::m_indexSolvent, HMWSoln::m_Lambda_nj_P, HMWSoln::m_molalitiesCropped, HMWSoln::m_Mu_nnn_P, HMWSoln::m_Phi_IJ_P, HMWSoln::m_PhiPhi_IJ_P, HMWSoln::m_Phiprime_IJ, HMWSoln::m_Psi_ijk_P, Constituents::m_speciesCharge, HMWSoln::m_Theta_ij_P, MolalityVPSSTP::m_weightSolvent, HMWSoln::pressure(), Constituents::speciesName(), and State::temperature().
Referenced by HMWSoln::s_update_dlnMolalityActCoeff_dP().
| void s_updatePitzer_dlnMolalityActCoeff_dT | ( | ) | const [private] |
Calculates the temperature derivative of the natural logarithm of the molality activity coefficients.
Public function makes sure that all dependent data is up to date, before calling a private function
Definition at line 3458 of file HMWSoln.cpp.
References HMWSoln::calc_lambdas(), HMWSoln::calc_thetas(), HMWSoln::counterIJ_setup(), HMWSoln::dA_DebyedT_TP(), DATA_PTR, HMWSoln::m_A_Debye, HMWSoln::m_Alpha1MX_ij, HMWSoln::m_Alpha2MX_ij, HMWSoln::m_Beta0MX_ij_L, HMWSoln::m_Beta1MX_ij_L, HMWSoln::m_Beta2MX_ij_L, HMWSoln::m_BMX_IJ_L, HMWSoln::m_BphiMX_IJ_L, HMWSoln::m_BprimeMX_IJ_L, HMWSoln::m_CMX_IJ_L, HMWSoln::m_CounterIJ, HMWSoln::m_CphiMX_ij_L, HMWSoln::m_debugCalc, HMWSoln::m_dlnActCoeffMolaldT_Unscaled, HMWSoln::m_g2func_IJ, HMWSoln::m_gamma_tmp, HMWSoln::m_gfunc_IJ, HMWSoln::m_h2func_IJ, HMWSoln::m_hfunc_IJ, HMWSoln::m_IionicMolality, MolalityVPSSTP::m_indexSolvent, HMWSoln::m_Lambda_nj_L, HMWSoln::m_molalitiesCropped, HMWSoln::m_Mu_nnn_L, HMWSoln::m_Phi_IJ_L, HMWSoln::m_PhiPhi_IJ_L, HMWSoln::m_Phiprime_IJ, HMWSoln::m_Psi_ijk_L, Constituents::m_speciesCharge, HMWSoln::m_Theta_ij_L, MolalityVPSSTP::m_weightSolvent, and Constituents::speciesName().
Referenced by HMWSoln::s_update_dlnMolalityActCoeff_dT().
| void s_updatePitzer_lnMolalityActCoeff | ( | ) | const [private] |
This function does the main pitzer coefficient calculation.
Definition at line 2362 of file HMWSoln.cpp.
References HMWSoln::calc_lambdas(), HMWSoln::calc_thetas(), HMWSoln::counterIJ_setup(), DATA_PTR, HMWSoln::m_A_Debye, HMWSoln::m_Alpha1MX_ij, HMWSoln::m_Alpha2MX_ij, HMWSoln::m_Beta0MX_ij, HMWSoln::m_Beta1MX_ij, HMWSoln::m_Beta2MX_ij, HMWSoln::m_BMX_IJ, HMWSoln::m_BphiMX_IJ, HMWSoln::m_BprimeMX_IJ, HMWSoln::m_CMX_IJ, HMWSoln::m_CounterIJ, HMWSoln::m_CphiMX_ij, HMWSoln::m_debugCalc, HMWSoln::m_g2func_IJ, HMWSoln::m_gamma_tmp, HMWSoln::m_gfunc_IJ, HMWSoln::m_h2func_IJ, HMWSoln::m_hfunc_IJ, HMWSoln::m_IionicMolality, MolalityVPSSTP::m_indexSolvent, HMWSoln::m_Lambda_nj, HMWSoln::m_lnActCoeffMolal_Unscaled, MolalityVPSSTP::m_molalities, HMWSoln::m_molalitiesCropped, HMWSoln::m_Mu_nnn, HMWSoln::m_Phi_IJ, HMWSoln::m_PhiPhi_IJ, HMWSoln::m_Phiprime_IJ, HMWSoln::m_Psi_ijk, Constituents::m_speciesCharge, HMWSoln::m_Theta_ij, MolalityVPSSTP::m_weightSolvent, MolalityVPSSTP::m_xmolSolventMIN, MAX, Phase::moleFraction(), Constituents::speciesName(), and State::temperature().
| void s_updateScaling_pHScaling | ( | ) | const [private] |
Apply the current phScale to a set of activity Coefficients.
See the Eq3/6 Manual for a thorough discussion.
Definition at line 6374 of file HMWSoln.cpp.
References AssertTrace, Cantera::fvo_copy_dbl_1(), MolalityVPSSTP::m_indexCLM, HMWSoln::m_lnActCoeffMolal_Scaled, HMWSoln::m_lnActCoeffMolal_Unscaled, MolalityVPSSTP::m_pHScalingType, Constituents::m_speciesCharge, Cantera::PHSCALE_NBS, Cantera::PHSCALE_PITZER, and HMWSoln::s_NBS_CLM_lnMolalityActCoeff().
| void s_updateScaling_pHScaling_dP | ( | ) | const [private] |
Apply the current phScale to a set of derivatives of the activity Coefficients wrt pressure.
See the Eq3/6 Manual for a thorough discussion of the need
Definition at line 6433 of file HMWSoln.cpp.
Referenced by HMWSoln::s_update_dlnMolalityActCoeff_dP().
| void s_updateScaling_pHScaling_dT | ( | ) | const [private] |
Apply the current phScale to a set of derivatives of the activity Coefficients wrt temperature.
See the Eq3/6 Manual for a thorough discussion of the need
Definition at line 6394 of file HMWSoln.cpp.
References AssertTrace, Cantera::fvo_copy_dbl_1(), HMWSoln::m_dlnActCoeffMolaldT_Scaled, HMWSoln::m_dlnActCoeffMolaldT_Unscaled, MolalityVPSSTP::m_indexCLM, MolalityVPSSTP::m_pHScalingType, Constituents::m_speciesCharge, Cantera::PHSCALE_NBS, Cantera::PHSCALE_PITZER, and HMWSoln::s_NBS_CLM_dlnMolalityActCoeff_dT().
Referenced by HMWSoln::s_update_dlnMolalityActCoeff_dT().
| void s_updateScaling_pHScaling_dT2 | ( | ) | const [private] |
Apply the current phScale to a set of 2nd derivatives of the activity Coefficients wrt temperature.
See the Eq3/6 Manual for a thorough discussion of the need
Definition at line 6414 of file HMWSoln.cpp.
References AssertTrace, Cantera::fvo_copy_dbl_1(), HMWSoln::m_d2lnActCoeffMolaldT2_Scaled, HMWSoln::m_d2lnActCoeffMolaldT2_Unscaled, MolalityVPSSTP::m_indexCLM, MolalityVPSSTP::m_pHScalingType, Constituents::m_speciesCharge, Cantera::PHSCALE_NBS, Cantera::PHSCALE_PITZER, and HMWSoln::s_NBS_CLM_d2lnMolalityActCoeff_dT2().
| doublereal satPressure | ( | doublereal | T | ) | const [virtual] |
Get the saturation pressure for a given temperature.
Note the limitations of this function. Stability considerations concernting multiphase equilibrium are ignored in this calculation. Therefore, the call is made directly to the SS of water underneath. The object is put back into its original state at the end of the call.
- Todo:
- This is probably not implemented correctly. The stability of the salt should be added into this calculation. The underlying water model may be called to get the stability of the pure water solution, if needed.
- Parameters:
-
T Temperature (kelvin)
Reimplemented from ThermoPhase.
Definition at line 1367 of file HMWSoln.cpp.
References HMWSoln::m_waterSS, HMWSoln::pressure(), PDSS::satPressure(), PDSS::setState_TP(), and State::temperature().
| virtual doublereal satTemperature | ( | doublereal | p | ) | const [inline, virtual] |
Return the saturation temperature given the pressure.
- Parameters:
-
p Pressure (Pa)
Reimplemented from ThermoPhase.
Definition at line 2016 of file HMWSoln.h.
References HMWSoln::err().
| void saveSpeciesData | ( | const int | k, | |
| const XML_Node *const | data | |||
| ) | [inherited] |
Store a reference pointer to the XML tree containing the species data for this phase.
The following methods are used in the process of constructing the phase and setting its parameters from a specification in an input file. They are not normally used in application programs. To see how they are used, see files importCTML.cpp and ThermoFactory.cpp.
This is used to access data needed to construct transport manager later.
For internal use only.
- Parameters:
-
k Species index data Pointer to the XML_Node data containing information about the species in the phase.
Definition at line 941 of file ThermoPhase.cpp.
References ThermoPhase::m_speciesData.
| void saveState | ( | int | lenstate, | |
| doublereal * | state | |||
| ) | const [inherited] |
Write to array 'state' the current internal state.
- Parameters:
-
lenstate length of the state array. Must be >= nSpecies() + 2 state output vector. Must be of length nSpecies() + 2 or greater.
Definition at line 144 of file Phase.cpp.
References State::density(), State::getMassFractions(), and State::temperature().
| void saveState | ( | vector_fp & | state | ) | const [inherited] |
Save the current internal state of the phase.
Write to vector 'state' the current internal state.
- Parameters:
-
state output vector. Will be resized to nSpecies() + 2 on return.
Definition at line 140 of file Phase.cpp.
References Constituents::nSpecies().
| void setConcentrations | ( | const doublereal *const | conc | ) | [virtual, inherited] |
Set the concentrations to the specified values within the phase.
We set the concentrations here and therefore we set the overall density of the phase. We hold the temperature constant during this operation. Therefore, we have possibly changed the pressure of the phase by calling this routine.
- Parameters:
-
conc The input vector to this routine is in dimensional units. For volumetric phases c[k] is the concentration of the kth species in kmol/m3. For surface phases, c[k] is the concentration in kmol/m2. The length of the vector is the number of species in the phase.
Reimplemented in IdealSolidSolnPhase.
Definition at line 196 of file State.cpp.
References State::m_kk, State::m_mmw, State::m_molwts, State::m_y, State::m_ym, State::setDensity(), and State::stateMFChangeCalc().
Referenced by SurfPhase::setCoverages(), and SurfPhase::setCoveragesNoNorm().
| void setDensity | ( | const doublereal | rho | ) | [virtual] |
Set the internally storred density (kg/m^3) of the phase.
Overwritten setDensity() function is necessary because of the underlying water model.
- Todo:
- Now have a compressible ss equation for liquid water. Therefore, this phase is compressible. May still want to change the independent variable however.
NOTE: This is an overwritten function from the State.h class
- Parameters:
-
rho Input density (kg/m^3).
Reimplemented from State.
Definition at line 833 of file HMWSoln.cpp.
References HMWSoln::density().
| void setElectricPotential | ( | doublereal | v | ) | [inline, inherited] |
Set the electric potential of this phase (V).
This is used by classes InterfaceKinetics and EdgeKinetics to compute the rates of charge-transfer reactions, and in computing the electrochemical potentials of the species.
Each phase may have its own electric potential.
- Parameters:
-
v Input value of the electric potential in Volts
Reimplemented in IdealMolalSoln.
Definition at line 995 of file ThermoPhase.h.
References ThermoPhase::m_phi.
| void setElementPotentials | ( | const vector_fp & | lambda | ) | [inherited] |
Stores the element potentials in the ThermoPhase object.
Called by function 'equilibrate' in ChemEquil.h to transfer the element potentials to this object after every successful equilibration routine. The element potentials are storred in their dimensionless forms, calculated by dividing by RT.
- Parameters:
-
lambda Input vector containing the element potentials. Length = nElements. Units are Joules/kmol.
Definition at line 993 of file ThermoPhase.cpp.
References Cantera::GasConstant, ThermoPhase::m_hasElementPotentials, ThermoPhase::m_lambdaRRT, Constituents::nElements(), and State::temperature().
| void setID | ( | std::string | id | ) | [inherited] |
Set the string id for the phase.
Sets the id of the phase. The ID of the phase is originally set to the string name of the phase within the XML file. Generally, it refers to the individual model name that denotes the species, the thermo, and the reaction rate info.
- Parameters:
-
id String id of the phase
Definition at line 120 of file Phase.cpp.
References Phase::m_id.
| void setIndex | ( | int | m | ) | [inline, inherited] |
For internal use only.
Set the index number. The Cantera interface library uses this method to set the index number to the location of the pointer to this object in the pointer array it maintains. Using this method for any other purpose will lead to unpredictable results if used in conjunction with the interface library.
- Parameters:
-
m Input the index number.
Reimplemented from Phase.
Definition at line 1998 of file ThermoPhase.h.
References ThermoPhase::m_index.
| void setMassFractions | ( | const doublereal *const | y | ) | [virtual, inherited] |
Set the mass fractions to the specified values, and then normalize them so that they sum to 1.0.
- Parameters:
-
y Array of unnormalized mass fraction values (input). Must have a length greater than or equal to the number of species. y Input vector of mass fractions. There is no restriction on the sum of the mass fraction vector. Internally, the State object will normalize this vector before storring its contents. Length is m_kk.
Reimplemented in IdealSolidSolnPhase.
Definition at line 142 of file State.cpp.
References State::m_kk, State::m_mmw, State::m_rmolwts, State::m_y, State::m_ym, Cantera::scale(), and State::stateMFChangeCalc().
Referenced by Phase::setMassFractionsByName(), ThermoPhase::setState_PY(), Phase::setState_RY(), ThermoPhase::setState_TPY(), Phase::setState_TRY(), and Phase::setState_TY().
| void setMassFractions_NoNorm | ( | const doublereal *const | y | ) | [virtual, inherited] |
Set the mass fractions to the specified values without normalizing.
This is useful when the normalization condition is being handled by some other means, for example by a constraint equation as part of a larger set of equations.
- Parameters:
-
y Input vector of mass fractions. Length is m_kk.
Reimplemented in IdealSolidSolnPhase.
Definition at line 167 of file State.cpp.
References State::m_kk, State::m_mmw, State::m_rmolwts, State::m_y, State::m_ym, and State::stateMFChangeCalc().
Referenced by Phase::restoreState().
| void setMassFractionsByName | ( | const std::string & | x | ) | [inherited] |
Set the species mass fractions by name.
Species not listed by name in x are set to zero.
- Parameters:
-
x String containing a composition map
Definition at line 204 of file Phase.cpp.
References Constituents::nSpecies(), Cantera::parseCompString(), Phase::setMassFractionsByName(), and Constituents::speciesName().
| void setMassFractionsByName | ( | compositionMap & | yMap | ) | [inherited] |
Set the species mass fractions by name.
- Parameters:
-
yMap map from species names to mass fraction values. Species not listed by name in yMapare set to zero.
Definition at line 193 of file Phase.cpp.
References Constituents::nSpecies(), State::setMassFractions(), and Constituents::speciesName().
Referenced by Phase::setMassFractionsByName(), ThermoPhase::setState_TPY(), Phase::setState_TRY(), and ThermoPhase::setStateFromXML().
| void setMolalities | ( | const doublereal *const | molal | ) | [inherited] |
Set the molalities of the solutes in a phase.
Note, the entry for the solvent is not used. We are supplied with the molalities of all of the solute species. We then calculate the mole fractions of all species and update the ThermoPhase object.
![\[ m_i = \frac{X_i}{M_o/1000 * X_{o,p}} \]](form_376.png)
where
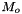 is the molecular weight of the solvent
is the molecular weight of the solvent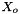 is the mole fraction of the solvent
is the mole fraction of the solvent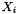 is the mole fraction of the solute.
is the mole fraction of the solute.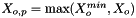
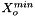 = minimum mole fraction of solvent allowed in the denominator.
= minimum mole fraction of solvent allowed in the denominator.
The formulas for calculating mole fractions are
![\[ L^{sum} = \frac{1}{\tilde{M}_o X_o} = \frac{1}{\tilde{M}_o} + \sum_{i\ne o} m_i \]](form_359.png)
Then,
![\[ X_o = \frac{1}{\tilde{M}_o L^{sum}} \]](form_360.png)
![\[ X_i = \frac{m_i}{L^{sum}} \]](form_361.png)
It is currently an error if the solvent mole fraction is attempted to be set to a value lower than 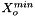 .
.
- Parameters:
-
molal Input vector of molalities. Length: m_kk.
Definition at line 268 of file MolalityVPSSTP.cpp.
References MolalityVPSSTP::calcMolalities(), DATA_PTR, MolalityVPSSTP::m_indexSolvent, Phase::m_kk, MolalityVPSSTP::m_Mnaught, MolalityVPSSTP::m_molalities, and State::setMoleFractions().
Referenced by MolalityVPSSTP::setState_TPM().
| void setMolalitiesByName | ( | const std::string & | name | ) | [inherited] |
Set the molalities of a phase.
Set the molalities of the solutes in a phase. Note, the entry for the solvent is not used.
- Parameters:
-
name String containing the information for a composition map.
Definition at line 391 of file MolalityVPSSTP.cpp.
References Constituents::nSpecies(), Cantera::parseCompString(), MolalityVPSSTP::setMolalitiesByName(), and Constituents::speciesName().
| void setMolalitiesByName | ( | compositionMap & | xMap | ) | [inherited] |
Set the molalities of a phase.
Set the molalities of the solutes in a phase. Note, the entry for the solvent is not used.
- Parameters:
-
xMap Composition Map containing the molalities.
Definition at line 305 of file MolalityVPSSTP.cpp.
References MolalityVPSSTP::calcMolalities(), Constituents::charge(), DATA_PTR, State::getMoleFractions(), MolalityVPSSTP::m_indexSolvent, MolalityVPSSTP::m_Mnaught, MolalityVPSSTP::m_xmolSolventMIN, Cantera::max(), Constituents::nSpecies(), State::setMoleFractions(), and Constituents::speciesName().
Referenced by MolalityVPSSTP::setMolalitiesByName(), MolalityVPSSTP::setState_TPM(), and MolalityVPSSTP::setStateFromXML().
| void setMolarDensity | ( | const doublereal | conc | ) | [virtual] |
Set the internally storred molar density (kmol/m^3) for the phase.
Overwritten setMolarDensity() function is necessary because of the underlying water model.
This function will now throw an error condition if the input isn't exactly equal to the current molar density.
NOTE: This is a virtual function overwritten from the State.h class
- Parameters:
-
conc Input molar density (kmol/m^3).
Reimplemented from State.
Definition at line 851 of file HMWSoln.cpp.
| void setMolecularWeight | ( | const int | k, | |
| const double | mw | |||
| ) | [inline, protected, inherited] |
Set the molecular weight of a single species to a given value.
- Parameters:
-
k id of the species mw Molecular Weight (kg kmol-1)
Definition at line 385 of file State.h.
References State::m_molwts, and State::m_rmolwts.
Referenced by WaterSSTP::initThermoXML().
| void setMoleFractions | ( | const doublereal *const | x | ) | [virtual, inherited] |
Set the mole fractions to the specified values, and then normalize them so that they sum to 1.0.
- Parameters:
-
x Array of unnormalized mole fraction values (input). Must have a length greater than or equal to the number of species. x Input vector of mole fractions. There is no restriction on the sum of the mole fraction vector. Internally, the State object will normalize this vector before storring its contents. Length is m_kk.
Reimplemented in IdealSolidSolnPhase.
Definition at line 102 of file State.cpp.
References Cantera::dot(), State::m_kk, State::m_mmw, State::m_molwts, State::m_y, State::m_ym, and State::stateMFChangeCalc().
Referenced by SingleSpeciesTP::initThermo(), WaterSSTP::initThermoXML(), MolalityVPSSTP::setMolalities(), MolalityVPSSTP::setMolalitiesByName(), Phase::setMoleFractionsByName(), ThermoPhase::setState_PX(), Phase::setState_RX(), Phase::setState_TNX(), ThermoPhase::setState_TPX(), Phase::setState_TRX(), and Phase::setState_TX().
| void setMoleFractions_NoNorm | ( | const doublereal *const | x | ) | [virtual, inherited] |
Set the mole fractions to the specified values without normalizing.
This is useful when the normalization condition is being handled by some other means, for example by a constraint equation as part of a larger set of equations.
- Parameters:
-
x Input vector of mole fractions. Length is m_kk.
Reimplemented in IdealSolidSolnPhase.
Definition at line 115 of file State.cpp.
References Cantera::dot(), State::m_kk, State::m_mmw, State::m_molwts, State::m_y, State::m_ym, and State::stateMFChangeCalc().
| void setMoleFractionsByName | ( | const std::string & | x | ) | [inherited] |
Set the mole fractions of a group of species by name.
The string x is in the form of a composition map Species which are not listed by name in the composition map are set to zero.
- Parameters:
-
x string x in the form of a composition map
Definition at line 177 of file Phase.cpp.
References Constituents::nSpecies(), Cantera::parseCompString(), Phase::setMoleFractionsByName(), and Constituents::speciesName().
| void setMoleFractionsByName | ( | compositionMap & | xMap | ) | [inherited] |
Set the species mole fractions by name.
- Parameters:
-
xMap map from species names to mole fraction values. Species not listed by name in xMapare set to zero.
Definition at line 166 of file Phase.cpp.
References Constituents::nSpecies(), State::setMoleFractions(), and Constituents::speciesName().
Referenced by Phase::setMoleFractionsByName(), ThermoPhase::setState_TPX(), Phase::setState_TRX(), and ThermoPhase::setStateFromXML().
| void setMoleFSolventMin | ( | doublereal | xmolSolventMIN | ) | [inherited] |
Sets the minimum mole fraction in the molality formulation.
Note the molality formulation is singular in the limit that the solvent mole fraction goes to zero. Numerically, how this limit is treated and resolved is an ongoing issue within Cantera.
- Parameters:
-
xmolSolventMIN Input double containing the minimum mole fraction
Definition at line 188 of file MolalityVPSSTP.cpp.
References MolalityVPSSTP::m_xmolSolventMIN.
Referenced by IdealMolalSoln::initThermoXML(), and HMWSoln::initThermoXML().
| void setName | ( | std::string | nm | ) | [inherited] |
Sets the string name for the phase.
Sets the name of the phase. The name of the phase is originally set to the string name of the phase within the XML file. Generally, it refers to the individual model name that denotes the species, the thermo, and the reaction rate info. It may also refer more specifically to a location within the domain.
- Parameters:
-
nm String name of the phase
Definition at line 128 of file Phase.cpp.
References Phase::m_name.
| void setNDim | ( | int | ndim | ) | [inline, inherited] |
Set the number of spatial dimensions (1, 2, or 3).
The number of spatial dimensions is used for vector involving directions.
- Parameters:
-
ndim Input number of dimensions.
Definition at line 484 of file Phase.h.
References Phase::m_ndim.
Referenced by EdgePhase::EdgePhase(), EdgePhase::operator=(), and SurfPhase::SurfPhase().
| void setParameters | ( | int | n, | |
| doublereal *const | c | |||
| ) | [virtual] |
Set the equation of state parameters.
For internal use only.
The number and meaning of these depends on the subclass.
- Parameters:
-
n number of parameters c array of n coefficients
Reimplemented from ThermoPhase.
Definition at line 1337 of file HMWSoln.cpp.
| void setParametersFromXML | ( | const XML_Node & | eosdata | ) | [virtual] |
Set equation of state parameter values from XML entries.
This method is called by function importPhase in file importCTML.cpp when processing a phase definition in an input file. It should be overloaded in subclasses to set any parameters that are specific to that particular phase model.
- Parameters:
-
eosdata An XML_Node object corresponding to the "thermo" entry for this phase in the input file.
Reimplemented from VPStandardStateTP.
Definition at line 1356 of file HMWSoln.cpp.
| void setpHScale | ( | const int | pHscaleType | ) | [inherited] |
Set the pH scale, which determines the scale for single-ion activity coefficients.
Single ion activity coefficients are not unique in terms of the representing actual measureable quantities.
- Parameters:
-
pHscaleType Integer representing the pHscale
Definition at line 139 of file MolalityVPSSTP.cpp.
References Cantera::int2str(), MolalityVPSSTP::m_pHScalingType, Cantera::PHSCALE_NBS, and Cantera::PHSCALE_PITZER.
| void setPressure | ( | doublereal | p | ) | [virtual] |
Set the internally storred pressure (Pa) at constant temperature and composition.
This method sets the pressure within the object. The water model is a completely compressible model. Also, the dielectric constant is pressure dependent.
- Parameters:
-
p input Pressure (Pa)
- Todo:
- Implement a variable pressure capability
Reimplemented from VPStandardStateTP.
Definition at line 758 of file HMWSoln.cpp.
| void setReferenceComposition | ( | const doublereal *const | x | ) | [virtual, inherited] |
Sets the reference composition.
- Parameters:
-
x Mole fraction vector to set the reference composition to. If this is zero, then the reference mole fraction is set to the current mole fraction vector.
Definition at line 891 of file ThermoPhase.cpp.
References DATA_PTR, State::getMoleFractions(), Phase::m_kk, and ThermoPhase::xMol_Ref.
Referenced by ThermoPhase::initThermoXML().
| void setSolvent | ( | int | k | ) | [inherited] |
This routine sets the index number of the solvent for the phase.
Note, having a solvent is a precursor to many things having to do with molality.
- Parameters:
-
k the solvent index number
Definition at line 164 of file MolalityVPSSTP.cpp.
References AssertThrowMsg, MolalityVPSSTP::m_indexSolvent, Phase::m_kk, MolalityVPSSTP::m_Mnaught, MolalityVPSSTP::m_weightSolvent, and Constituents::molecularWeight().
Referenced by MolalityVPSSTP::initThermo(), MolalityVPSSTP::initThermoXML(), and HMWSoln::initThermoXML().
| void setSpeciesThermo | ( | SpeciesThermo * | spthermo | ) | [inline, inherited] |
Install a species thermodynamic property manager.
The species thermodynamic property manager computes properties of the pure species for use in constructing solution properties. It is meant for internal use, and some classes derived from ThermoPhase may not use any species thermodynamic property manager. This method is called by function importPhase() in importCTML.cpp.
- Parameters:
-
spthermo input pointer to the species thermodynamic property manager.
For internal use only.
Definition at line 1887 of file ThermoPhase.h.
References ThermoPhase::m_spthermo.
Referenced by VPSSMgrFactory::newVPSSMgr().
| void setState_HP | ( | doublereal | h, | |
| doublereal | p, | |||
| doublereal | tol = 1.e-4 | |||
| ) | [virtual, inherited] |
Set the internally storred specific enthalpy (J/kg) and pressure (Pa) of the phase.
- Parameters:
-
h Specific enthalpy (J/kg) p Pressure (Pa) tol Optional parameter setting the tolerance of the calculation. Defaults to 1.0E-4
Reimplemented in PureFluidPhase, and SingleSpeciesTP.
Definition at line 238 of file ThermoPhase.cpp.
References ThermoPhase::setState_HPorUV().
| virtual void setState_Psat | ( | doublereal | p, | |
| doublereal | x | |||
| ) | [inline, virtual] |
Set the state to a saturated system at a particular pressure.
- Parameters:
-
p Pressure (Pa) x Fraction of vapor
Reimplemented from ThermoPhase.
Definition at line 2045 of file HMWSoln.h.
References HMWSoln::err().
| void setState_PX | ( | doublereal | p, | |
| doublereal * | x | |||
| ) | [inherited] |
Set the pressure (Pa) and mole fractions.
Note, the mole fractions are set first before the pressure is set. Setting the pressure may involve the solution of a nonlinear equation.
- Parameters:
-
p Pressure (Pa) x Vector of mole fractions. Length is equal to m_kk.
Reimplemented in SingleSpeciesTP.
Definition at line 230 of file ThermoPhase.cpp.
References State::setMoleFractions(), and ThermoPhase::setPressure().
Referenced by IdealSolnGasVPSS::setToEquilState(), IdealSolidSolnPhase::setToEquilState(), and IdealGasPhase::setToEquilState().
| void setState_PY | ( | doublereal | p, | |
| doublereal * | y | |||
| ) | [inherited] |
Set the internally storred pressure (Pa) and mass fractions.
Note, the temperature is held constant during this operation. Note, the mass fractions are set first before the pressure is set. Setting the pressure may involve the solution of a nonlinear equation.
- Parameters:
-
p Pressure (Pa) y Vector of mass fractions. Length is equal to m_kk.
Reimplemented in SingleSpeciesTP.
Definition at line 234 of file ThermoPhase.cpp.
References State::setMassFractions(), and ThermoPhase::setPressure().
| void setState_RX | ( | doublereal | rho, | |
| doublereal * | x | |||
| ) | [inherited] |
Set the density (kg/m^3) and mole fractions.
- Parameters:
-
rho Density (kg/m^3) x vector of species mole fractions. Length is equal to m_kk
Definition at line 259 of file Phase.cpp.
References State::setDensity(), and State::setMoleFractions().
| void setState_RY | ( | doublereal | rho, | |
| doublereal * | y | |||
| ) | [inherited] |
Set the density (kg/m^3) and mass fractions.
- Parameters:
-
rho Density (kg/m^3) y vector of species mass fractions. Length is equal to m_kk
Definition at line 264 of file Phase.cpp.
References State::setDensity(), and State::setMassFractions().
| void setState_SP | ( | doublereal | s, | |
| doublereal | p, | |||
| doublereal | tol = 1.e-4 | |||
| ) | [virtual, inherited] |
Set the specific entropy (J/kg/K) and pressure (Pa).
This function fixes the internal state of the phase so that the specific entropy and the pressure have the value of the input parameters.
- Parameters:
-
s specific entropy (J/kg/K) p specific pressure (Pa). tol Optional parameter setting the tolerance of the calculation. Defaults to 1.0E-4
Reimplemented in PureFluidPhase, and SingleSpeciesTP.
Definition at line 512 of file ThermoPhase.cpp.
References ThermoPhase::setState_SPorSV().
| void setState_SV | ( | doublereal | s, | |
| doublereal | v, | |||
| doublereal | tol = 1.e-4 | |||
| ) | [virtual, inherited] |
Set the specific entropy (J/kg/K) and specific volume (m^3/kg).
This function fixes the internal state of the phase so that the specific entropy and specific volume have the value of the input parameters.
- Parameters:
-
s specific entropy (J/kg/K) v specific volume (m^3/kg). tol Optional parameter setting the tolerance of the calculation. Defaults to 1.0E-4
Reimplemented in PureFluidPhase, and SingleSpeciesTP.
Definition at line 517 of file ThermoPhase.cpp.
References ThermoPhase::setState_SPorSV().
| void setState_TNX | ( | doublereal | t, | |
| doublereal | n, | |||
| const doublereal * | x | |||
| ) | [inherited] |
Set the internally storred temperature (K), molar density (kmol/m^3), and mole fractions.
Note, the mole fractions are always set first, before the molar density
- Parameters:
-
t Temperature in kelvin n molar density (kmol/m^3) x vector of species mole fractions. Length is equal to m_kk
Definition at line 220 of file Phase.cpp.
References State::setMolarDensity(), State::setMoleFractions(), and State::setTemperature().
| void setState_TP | ( | doublereal | t, | |
| doublereal | p | |||
| ) | [virtual] |
Set the temperature (K) and pressure (Pa).
Set the temperature and pressure.
- Parameters:
-
t Temperature (K) p Pressure (Pa)
Reimplemented from VPStandardStateTP.
Definition at line 870 of file HMWSoln.cpp.
Referenced by HMWSoln::calcDensity().
| void setState_TPM | ( | doublereal | t, | |
| doublereal | p, | |||
| const std::string & | m | |||
| ) | [inherited] |
Set the temperature (K), pressure (Pa), and molalities.
- Parameters:
-
t Temperature (K) p Pressure (Pa) m String which gets translated into a composition map for the molalities of the solutes.
Definition at line 623 of file MolalityVPSSTP.cpp.
References MolalityVPSSTP::setMolalitiesByName(), and VPStandardStateTP::setState_TP().
| void setState_TPM | ( | doublereal | t, | |
| doublereal | p, | |||
| compositionMap & | m | |||
| ) | [inherited] |
Set the temperature (K), pressure (Pa), and molalities.
- Parameters:
-
t Temperature (K) p Pressure (Pa) m compositionMap containing the molalities
Definition at line 615 of file MolalityVPSSTP.cpp.
References MolalityVPSSTP::setMolalitiesByName(), and VPStandardStateTP::setState_TP().
| void setState_TPM | ( | doublereal | t, | |
| doublereal | p, | |||
| const doublereal *const | molalities | |||
| ) | [inherited] |
Set the temperature (K), pressure (Pa), and molalities (gmol kg-1) of the solutes.
- Parameters:
-
t Temperature (K) p Pressure (Pa) molalities Input vector of molalities of the solutes. Length: m_kk.
Definition at line 606 of file MolalityVPSSTP.cpp.
References MolalityVPSSTP::setMolalities(), and VPStandardStateTP::setState_TP().
| void setState_TPX | ( | doublereal | t, | |
| doublereal | p, | |||
| const std::string & | x | |||
| ) | [inherited] |
Set the temperature (K), pressure (Pa), and mole fractions.
Note, the mole fractions are set first before the pressure is set. Setting the pressure may involve the solution of a nonlinear equation.
- Parameters:
-
t Temperature (K) p Pressure (Pa) x String containing a composition map of the mole fractions. Species not in the composition map are assumed to have zero mole fraction
Reimplemented in SingleSpeciesTP.
Definition at line 186 of file ThermoPhase.cpp.
References Constituents::nSpecies(), Cantera::parseCompString(), Phase::setMoleFractionsByName(), ThermoPhase::setPressure(), State::setTemperature(), and Constituents::speciesName().
| void setState_TPX | ( | doublereal | t, | |
| doublereal | p, | |||
| compositionMap & | x | |||
| ) | [inherited] |
Set the temperature (K), pressure (Pa), and mole fractions.
Note, the mole fractions are set first before the pressure is set. Setting the pressure may involve the solution of a nonlinear equation.
- Parameters:
-
t Temperature (K) p Pressure (Pa) x Composition map of mole fractions. Species not in the composition map are assumed to have zero mole fraction
Reimplemented in SingleSpeciesTP.
Definition at line 181 of file ThermoPhase.cpp.
References Phase::setMoleFractionsByName(), ThermoPhase::setPressure(), and State::setTemperature().
| void setState_TPX | ( | doublereal | t, | |
| doublereal | p, | |||
| const doublereal * | x | |||
| ) | [inherited] |
Set the temperature (K), pressure (Pa), and mole fractions.
Note, the mole fractions are set first before the pressure is set. Setting the pressure may involve the solution of a nonlinear equation.
- Parameters:
-
t Temperature (K) p Pressure (Pa) x Vector of mole fractions. Length is equal to m_kk.
Reimplemented in SingleSpeciesTP.
Definition at line 176 of file ThermoPhase.cpp.
References State::setMoleFractions(), ThermoPhase::setPressure(), and State::setTemperature().
Referenced by MultiPhase::setMoles(), and MultiPhase::setPhaseMoleFractions().
| void setState_TPY | ( | doublereal | t, | |
| doublereal | p, | |||
| const std::string & | y | |||
| ) | [inherited] |
Set the internally storred temperature (K), pressure (Pa), and mass fractions of the phase.
Note, the mass fractions are set first before the pressure is set. Setting the pressure may involve the solution of a nonlinear equation.
- Parameters:
-
t Temperature (K) p Pressure (Pa) y String containing a composition map of the mass fractions. Species not in the composition map are assumed to have zero mass fraction
Reimplemented in SingleSpeciesTP.
Definition at line 211 of file ThermoPhase.cpp.
References Constituents::nSpecies(), Cantera::parseCompString(), Phase::setMassFractionsByName(), ThermoPhase::setPressure(), State::setTemperature(), and Constituents::speciesName().
| void setState_TPY | ( | doublereal | t, | |
| doublereal | p, | |||
| compositionMap & | y | |||
| ) | [inherited] |
Set the internally storred temperature (K), pressure (Pa), and mass fractions of the phase.
Note, the mass fractions are set first before the pressure is set. Setting the pressure may involve the solution of a nonlinear equation.
- Parameters:
-
t Temperature (K) p Pressure (Pa) y Composition map of mass fractions. Species not in the composition map are assumed to have zero mass fraction
Reimplemented in SingleSpeciesTP.
Definition at line 206 of file ThermoPhase.cpp.
References Phase::setMassFractionsByName(), ThermoPhase::setPressure(), and State::setTemperature().
| void setState_TPY | ( | doublereal | t, | |
| doublereal | p, | |||
| const doublereal * | y | |||
| ) | [inherited] |
Set the internally storred temperature (K), pressure (Pa), and mass fractions of the phase.
Note, the mass fractions are set first before the pressure is set. Setting the pressure may involve the solution of a nonlinear equation.
- Parameters:
-
t Temperature (K) p Pressure (Pa) y Vector of mass fractions. Length is equal to m_kk.
Reimplemented in SingleSpeciesTP.
Definition at line 201 of file ThermoPhase.cpp.
References State::setMassFractions(), ThermoPhase::setPressure(), and State::setTemperature().
| void setState_TR | ( | doublereal | t, | |
| doublereal | rho | |||
| ) | [inherited] |
Set the internally storred temperature (K) and density (kg/m^3).
Set the temperature (K) and density (kg/m^3).
- Parameters:
-
t Temperature in kelvin rho Density (kg/m^3)
Definition at line 244 of file Phase.cpp.
References State::setDensity(), and State::setTemperature().
| void setState_TRX | ( | doublereal | t, | |
| doublereal | dens, | |||
| compositionMap & | x | |||
| ) | [inherited] |
Set the internally storred temperature (K), density, and mole fractions.
Set the temperature (K), density (kg/m^3), and mole fractions.
Note, the mole fractions are always set first, before the density
- Parameters:
-
t Temperature in kelvin dens Density (kg/m^3) x Composition Map containing the mole fractions. Species not included in the map are assumed to have a zero mole fraction.
Definition at line 226 of file Phase.cpp.
References State::setDensity(), Phase::setMoleFractionsByName(), and State::setTemperature().
| void setState_TRX | ( | doublereal | t, | |
| doublereal | dens, | |||
| const doublereal * | x | |||
| ) | [inherited] |
Set the internally storred temperature (K), density, and mole fractions.
Set the temperature (K), density (kg/m^3), and mole fractions.
Note, the mole fractions are always set first, before the density
- Parameters:
-
t Temperature in kelvin dens Density (kg/m^3) x vector of species mole fractions. Length is equal to m_kk
Definition at line 215 of file Phase.cpp.
References State::setDensity(), State::setMoleFractions(), and State::setTemperature().
| void setState_TRY | ( | doublereal | t, | |
| doublereal | dens, | |||
| compositionMap & | y | |||
| ) | [inherited] |
Set the internally storred temperature (K), density, and mass fractions.
Set the temperature (K), density (kg/m^3), and mass fractions.
Note, the mass fractions are always set first, before the density
- Parameters:
-
t Temperature in kelvin dens Density (kg/m^3) y Composition Map containing the mass fractions. Species not included in the map are assumed to have a zero mass fraction.
Definition at line 238 of file Phase.cpp.
References State::setDensity(), Phase::setMassFractionsByName(), and State::setTemperature().
| void setState_TRY | ( | doublereal | t, | |
| doublereal | dens, | |||
| const doublereal * | y | |||
| ) | [inherited] |
Set the internally storred temperature (K), density, and mass fractions.
Set the temperature (K), density (kg/m^3), and mass fractions.
Note, the mass fractions are always set first, before the density
- Parameters:
-
t Temperature in kelvin dens Density (kg/m^3) y vector of species mass fractions. Length is equal to m_kk
Definition at line 232 of file Phase.cpp.
References State::setDensity(), State::setMassFractions(), and State::setTemperature().
| virtual void setState_Tsat | ( | doublereal | t, | |
| doublereal | x | |||
| ) | [inline, virtual] |
Set the state to a saturated system at a particular temperature.
- Parameters:
-
t Temperature (kelvin) x Fraction of vapor
Reimplemented from ThermoPhase.
Definition at line 2041 of file HMWSoln.h.
References HMWSoln::err().
| void setState_TX | ( | doublereal | t, | |
| doublereal * | x | |||
| ) | [inherited] |
Set the internally storred temperature (K) and mole fractions.
Set the temperature (K) and mole fractions.
- Parameters:
-
t Temperature in kelvin x vector of species mole fractions. Length is equal to m_kk
Definition at line 249 of file Phase.cpp.
References State::setMoleFractions(), and State::setTemperature().
| void setState_TY | ( | doublereal | t, | |
| doublereal * | y | |||
| ) | [inherited] |
Set the internally storred temperature (K) and mass fractions.
Set the temperature (K) and mass fractions.
- Parameters:
-
t Temperature in kelvin y vector of species mass fractions. Length is equal to m_kk
Definition at line 254 of file Phase.cpp.
References State::setMassFractions(), and State::setTemperature().
| void setState_UV | ( | doublereal | u, | |
| doublereal | v, | |||
| doublereal | tol = 1.e-4 | |||
| ) | [virtual, inherited] |
Set the specific internal energy (J/kg) and specific volume (m^3/kg).
This function fixes the internal state of the phase so that the specific internal energy and specific volume have the value of the input parameters.
- Parameters:
-
u specific internal energy (J/kg) v specific volume (m^3/kg). tol Optional parameter setting the tolerance of the calculation. Defaults to 1.0E-4
Reimplemented in PureFluidPhase, and SingleSpeciesTP.
Definition at line 243 of file ThermoPhase.cpp.
References ThermoPhase::setState_HPorUV().
| void setStateFromXML | ( | const XML_Node & | state | ) | [virtual, inherited] |
Set equation of state parameter values from XML entries.
This method is called by function importPhase() in file importCTML.cpp when processing a phase definition in an input file. It should be overloaded in subclasses to set any parameters that are specific to that particular phase model.
The MolalityVPSSTP object defines a new method for setting the concentrations of a phase. The new method is defined by a block called "soluteMolalities". If this block is found, the concentrations within that phase are set to the "name":"molalities pairs found within that XML block. The solvent concentration is then set to everything else.
The function first calls the overloaded function , VPStandardStateTP::setStateFromXML(), to pick up the parent class behavior.
usage: Overloaded functions should call this function before carrying out their own behavior.
- Parameters:
-
state An XML_Node object corresponding to the "state" entry for this phase in the input file.
Reimplemented from ThermoPhase.
Definition at line 590 of file MolalityVPSSTP.cpp.
References ctml::getChildValue(), ctml::getFloat(), XML_Node::hasChild(), MolalityVPSSTP::setMolalitiesByName(), and VPStandardStateTP::setPressure().
Referenced by IdealMolalSoln::initThermoXML(), and DebyeHuckel::initThermoXML().
| void setTemperature | ( | const doublereal | temp | ) | [virtual] |
Set the temperature (K).
Overwritten setTemperature(double) from State.h. This function sets the temperature, and makes sure that the value propagates to underlying objects, such as the water standard state model.
- Todo:
- Make State::setTemperature a virtual function
- Parameters:
-
temp Temperature in kelvin
Reimplemented from VPStandardStateTP.
Definition at line 861 of file HMWSoln.cpp.
| virtual void setToEquilState | ( | const doublereal * | lambda_RT | ) | [inline, virtual] |
This method is used by the ChemEquil equilibrium solver.
It sets the state such that the chemical potentials satisfy
![\[ \frac{\mu_k}{\hat R T} = \sum_m A_{k,m} \left(\frac{\lambda_m} {\hat R T}\right) \]](form_18.png)
where 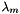 is the element potential of element m. The temperature is unchanged. Any phase (ideal or not) that implements this method can be equilibrated by ChemEquil.
is the element potential of element m. The temperature is unchanged. Any phase (ideal or not) that implements this method can be equilibrated by ChemEquil.
- Parameters:
-
lambda_RT Input vector of dimensionless element potentials The length is equal to nElements().
Reimplemented from MolalityVPSSTP.
Definition at line 1947 of file HMWSoln.h.
References HMWSoln::err(), and VPStandardStateTP::updateStandardStateThermo().
| void setVPSSMgr | ( | VPSSMgr * | vp_ptr | ) | [inherited] |
set the VPSS Mgr
- Parameters:
-
vp_ptr Pointer to the manager
Definition at line 362 of file VPStandardStateTP.cpp.
References VPStandardStateTP::m_VPSS_ptr.
| doublereal size | ( | int | k | ) | const [inline, inherited] |
This routine returns the size of species k.
- Parameters:
-
k index of the species
- Returns:
- Returns the size of the species. Units are meters.
Definition at line 309 of file Constituents.h.
References Constituents::m_speciesSize.
Referenced by IdealSolidSolnPhase::constructPhaseXML(), IdealMolalSoln::constructPhaseXML(), HMWSoln::constructPhaseXML(), DebyeHuckel::constructPhaseXML(), SurfPhase::getCoverages(), SurfPhase::initThermo(), IdealMolalSoln::initThermoXML(), SurfPhase::setCoverages(), SurfPhase::setCoveragesNoNorm(), and SurfPhase::standardConcentration().
| int solventIndex | ( | ) | const [inherited] |
Returns the solvent index.
Definition at line 179 of file MolalityVPSSTP.cpp.
References MolalityVPSSTP::m_indexSolvent.
| const std::vector< const XML_Node * > & speciesData | ( | ) | const [inherited] |
Return a pointer to the vector of XML nodes containing the species data for this phase.
Return a pointer to the XML tree containing the species data for this phase.
Definition at line 950 of file ThermoPhase.cpp.
References Phase::m_kk, and ThermoPhase::m_speciesData.
Referenced by MineralEQ3::initThermoXML(), HMWSoln::initThermoXML(), and DebyeHuckel::initThermoXML().
| bool speciesFrozen | ( | ) | [inline, inherited] |
True if freezeSpecies has been called.
Definition at line 318 of file Constituents.h.
References Constituents::m_speciesFrozen.
| int speciesIndex | ( | std::string | name | ) | const [inherited] |
Index of species named 'name'.
The first species added will have index 0, and the last one index nSpecies() - 1.
- Parameters:
-
name String name of the species
- Returns:
- Returns the index of the species.
Definition at line 414 of file Constituents.cpp.
References Constituents::m_speciesNames.
Referenced by HMWSoln::HMWSoln(), HMWSoln::initThermoXML(), DebyeHuckel::initThermoXML(), Kinetics::kineticsSpeciesIndex(), Phase::massFraction(), Phase::moleFraction(), HMWSoln::readXMLBinarySalt(), HMWSoln::readXMLLambdaNeutral(), HMWSoln::readXMLMunnnNeutral(), HMWSoln::readXMLPsiCommonAnion(), HMWSoln::readXMLPsiCommonCation(), HMWSoln::readXMLThetaAnion(), HMWSoln::readXMLThetaCation(), HMWSoln::readXMLZetaCation(), MolalityVPSSTP::report(), and Kinetics::speciesPhase().
| double speciesMolarVolume | ( | int | k | ) | const |
Report the molar volume of species k.
units - 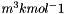
- Parameters:
-
k species index
- Deprecated:
- The getPartialMolarVolumes() expression is more precise.
Definition at line 1383 of file HMWSoln.cpp.
| string speciesName | ( | int | k | ) | const [inherited] |
Name of the species with index k.
- Parameters:
-
k index of the species
Definition at line 434 of file Constituents.cpp.
References Constituents::m_speciesNames, and Constituents::nSpecies().
Referenced by MolalityVPSSTP::findCLMIndex(), Phase::getMoleFractionsByName(), MultiPhase::init(), IdealMolalSoln::initThermoXML(), HMWSoln::initThermoXML(), DebyeHuckel::initThermoXML(), Kinetics::kineticsSpeciesName(), HMWSoln::readXMLBinarySalt(), ThermoPhase::report(), PureFluidPhase::report(), MolalityVPSSTP::report(), vcs_MultiPhaseEquil::reportCSV(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), HMWSoln::s_updatePitzer_lnMolalityActCoeff(), SurfPhase::setCoveragesByName(), Phase::setMassFractionsByName(), MolalityVPSSTP::setMolalitiesByName(), Phase::setMoleFractionsByName(), ThermoPhase::setState_TPX(), and ThermoPhase::setState_TPY().
| const vector< string > & speciesNames | ( | ) | const [inherited] |
Return a const referernce to the vector of species names.
Definition at line 447 of file Constituents.cpp.
References Constituents::m_speciesNames.
Referenced by PDSS_SSVol::constructPDSSFile(), PDSS_HKFT::constructPDSSFile(), PDSS_ConstVol::constructPDSSFile(), VPSSMgr_Water_HKFT::initThermoXML(), VPSSMgr_Water_ConstVol::initThermoXML(), VPSSMgr_ConstVol::initThermoXML(), IdealSolidSolnPhase::initThermoXML(), IdealMolalSoln::initThermoXML(), HMWSoln::initThermoXML(), and DebyeHuckel::initThermoXML().
| SpeciesThermo& speciesThermo | ( | ) | [inline] |
Return a reference to the species thermodynamic property manager.
- Todo:
- This method will fail if no species thermo manager has been installed.
Reimplemented from ThermoPhase.
Definition at line 2063 of file HMWSoln.h.
References ThermoPhase::m_spthermo.
| doublereal standardConcentration | ( | int | k = 0 |
) | const [virtual] |
Return the standard concentration for the kth species.
The standard concentration 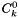 used to normalize the activity (i.e., generalized) concentration for use
used to normalize the activity (i.e., generalized) concentration for use
We have set the standard concentration for all solute species in this phase equal to the default concentration of the solvent at the system temperature and pressure multiplied by Mnaught (kg solvent / gmol solvent). The solvent standard concentration is just equal to its standard state concentration.
![\[ C_j^0 = C^o_o \tilde{M}_o \quad and C_o^0 = C^o_o \]](form_221.png)
The consequence of this is that the standard concentrations have unequal units between the solvent and the solute. However, both the solvent and the solute activity concentrations will have the same units of kmol kg-3.
This means that the kinetics operator essentially works on an generalized concentration basis (kmol / m3), with units for the kinetic rate constant specified as if all reactants (solvent or solute) are on a concentration basis (kmol /m3). The concentration will be modified by the activity coefficients.
For example, a bulk-phase binary reaction between liquid solute species j and k, producing a new liquid solute species l would have the following equation for its rate of progress variable, 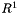 , which has units of kmol m-3 s-1.
, which has units of kmol m-3 s-1.
![\[ R^1 = k^1 C_j^a C_k^a = k^1 (C^o_o \tilde{M}_o a_j) (C^o_o \tilde{M}_o a_k) \]](form_209.png)
where
![\[ C_j^a = C^o_o \tilde{M}_o a_j \quad and \quad C_k^a = C^o_o \tilde{M}_o a_k \]](form_210.png)
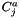 is the activity concentration of species j, and
is the activity concentration of species j, and 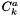 is the activity concentration of species k.
is the activity concentration of species k. 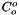 is the concentration of water at 298 K and 1 atm.
is the concentration of water at 298 K and 1 atm. 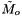 has units of kg solvent per gmol solvent and is equal to
has units of kg solvent per gmol solvent and is equal to
![\[ \tilde{M}_o = \frac{M_o}{1000} \]](form_213.png)
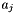 is the activity of species j at the current temperature and pressure and concentration of the liquid phase is given by the molality based activity coefficient multiplied by the molality of the jth species.
is the activity of species j at the current temperature and pressure and concentration of the liquid phase is given by the molality based activity coefficient multiplied by the molality of the jth species.
![\[ a_j = \gamma_j^\triangle m_j = \gamma_j^\triangle \frac{n_j}{\tilde{M}_o n_o} \]](form_214.png)
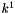 has units of m3 kmol-1 s-1.
has units of m3 kmol-1 s-1.
Therefore the generalized activity concentration of a solute species has the following form
![\[ C_j^a = C^o_o \frac{\gamma_j^\triangle n_j}{n_o} \]](form_215.png)
The generalized activity concentration of the solvent has the same units, but its a simpler form
![\[ C_o^a = C^o_o a_o \]](form_216.png)
- Parameters:
-
k Optional parameter indicating the species. The default is to assume this refers to species 0.
- Returns:
- Returns the standard Concentration in units of m3 kmol-1.
- Parameters:
-
k Species index
Reimplemented from MolalityVPSSTP.
Definition at line 946 of file HMWSoln.cpp.
References DATA_PTR, VPStandardStateTP::getStandardVolumes(), MolalityVPSSTP::m_indexSolvent, MolalityVPSSTP::m_Mnaught, and HMWSoln::m_tmpV.
Referenced by HMWSoln::getActivityConcentrations().
| int standardStateConvention | ( | ) | const [virtual, inherited] |
This method returns the convention used in specification of the standard state, of which there are currently two, temperature based, and variable pressure based.
Currently, there are two standard state conventions:
- Temperature-based activities cSS_CONVENTION_TEMPERATURE 0
- default
- Variable Pressure and Temperature -based activities cSS_CONVENTION_VPSS 1
Reimplemented from ThermoPhase.
Definition at line 169 of file VPStandardStateTP.cpp.
References Cantera::cSS_CONVENTION_VPSS.
| void stateMFChangeCalc | ( | bool | forceChange = false |
) | [inline, inherited] |
Every time the mole fractions have changed, this routine will increment the stateMFNumber.
- Parameters:
-
forceChange If this is true then the stateMFNumber always changes. This defaults to false.
Definition at line 31 of file State.cpp.
References State::m_stateNum.
Referenced by State::setConcentrations(), State::setMassFractions(), State::setMassFractions_NoNorm(), State::setMoleFractions(), and State::setMoleFractions_NoNorm().
| int stateMFNumber | ( | ) | const [inline, inherited] |
Return the state number.
Return the State Mole Fraction Number.
Definition at line 445 of file State.h.
References State::m_stateNum.
| doublereal sum_xlogQ | ( | doublereal *const | Q | ) | const [inherited] |
Evaluate 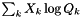 .
.
- Parameters:
-
Q Vector of length m_kk to take the log average of
- Returns:
- Returns the indicated sum.
Definition at line 188 of file State.cpp.
References State::m_mmw, and State::m_ym.
| doublereal sum_xlogx | ( | ) | const [inherited] |
Evaluate 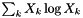 .
.
- Returns:
- returns the indicated sum. units are dimensionless.
Definition at line 184 of file State.cpp.
References State::m_mmw, and State::m_ym.
Referenced by IdealSolnGasVPSS::entropy_mole(), IdealSolidSolnPhase::entropy_mole(), IdealGasPhase::entropy_mole(), and IdealSolidSolnPhase::gibbs_mole().
| doublereal temperature | ( | ) | const [inline, inherited] |
Temperature (K).
Definition at line 309 of file State.h.
References State::m_temp.
Referenced by ThermoPhase::_RT(), VPStandardStateTP::_updateStandardStateThermo(), SurfPhase::_updateThermo(), SingleSpeciesTP::_updateThermo(), IdealSolidSolnPhase::_updateThermo(), IdealGasPhase::_updateThermo(), HMWSoln::A_Debye_TP(), DebyeHuckel::A_Debye_TP(), MultiPhase::addPhase(), HMWSoln::ADebye_J(), HMWSoln::ADebye_L(), HMWSoln::ADebye_V(), IdealSolnGasVPSS::calcDensity(), HMWSoln::calcDensity(), LatticePhase::cp_mole(), ConstDensityThermo::cp_mole(), SingleSpeciesTP::cv_mole(), HMWSoln::d2A_DebyedT2_TP(), DebyeHuckel::d2A_DebyedT2_TP(), HMWSoln::dA_DebyedP_TP(), DebyeHuckel::dA_DebyedP_TP(), HMWSoln::dA_DebyedT_TP(), DebyeHuckel::dA_DebyedT_TP(), WaterSSTP::dthermalExpansionCoeffdT(), IdealSolnGasVPSS::enthalpy_mole(), IdealSolidSolnPhase::enthalpy_mole(), IdealGasPhase::enthalpy_mole(), SurfPhase::getChemPotentials(), IdealSolnGasVPSS::getChemPotentials(), IdealSolidSolnPhase::getChemPotentials(), IdealMolalSoln::getChemPotentials(), IdealGasPhase::getChemPotentials(), HMWSoln::getChemPotentials(), DebyeHuckel::getChemPotentials(), SingleSpeciesTP::getChemPotentials_RT(), IdealSolidSolnPhase::getChemPotentials_RT(), WaterSSTP::getCp_R_ref(), ThermoPhase::getElementPotentials(), WaterSSTP::getEnthalpy_RT(), SurfPhase::getEnthalpy_RT(), StoichSubstanceSSTP::getEnthalpy_RT(), MineralEQ3::getEnthalpy_RT(), IdealSolidSolnPhase::getEnthalpy_RT(), WaterSSTP::getEnthalpy_RT_ref(), WaterSSTP::getEntropy_R_ref(), SingleSpeciesTP::getGibbs_ref(), IdealSolidSolnPhase::getGibbs_ref(), WaterSSTP::getGibbs_RT(), SurfPhase::getGibbs_RT(), WaterSSTP::getGibbs_RT_ref(), StoichSubstanceSSTP::getIntEnergy_RT(), MineralEQ3::getIntEnergy_RT(), IdealSolidSolnPhase::getIntEnergy_RT(), StoichSubstanceSSTP::getIntEnergy_RT_ref(), MineralEQ3::getIntEnergy_RT_ref(), MetalSHEelectrons::getIntEnergy_RT_ref(), IdealSolidSolnPhase::getIntEnergy_RT_ref(), HMWSoln::getPartialMolarCp(), DebyeHuckel::getPartialMolarCp(), SurfPhase::getPartialMolarEnthalpies(), SingleSpeciesTP::getPartialMolarEnthalpies(), IdealSolnGasVPSS::getPartialMolarEnthalpies(), IdealSolidSolnPhase::getPartialMolarEnthalpies(), IdealGasPhase::getPartialMolarEnthalpies(), HMWSoln::getPartialMolarEnthalpies(), DebyeHuckel::getPartialMolarEnthalpies(), HMWSoln::getPartialMolarEntropies(), DebyeHuckel::getPartialMolarEntropies(), SingleSpeciesTP::getPartialMolarIntEnergies(), IdealSolnGasVPSS::getPartialMolarIntEnergies(), IdealGasPhase::getPartialMolarIntEnergies(), HMWSoln::getPartialMolarVolumes(), DebyeHuckel::getPartialMolarVolumes(), SingleSpeciesTP::getPureGibbs(), WaterSSTP::getStandardChemPotentials(), StoichSubstanceSSTP::getStandardChemPotentials(), MineralEQ3::getStandardChemPotentials(), MetalSHEelectrons::getStandardChemPotentials(), IdealGasPhase::getStandardChemPotentials(), WaterSSTP::getStandardVolumes_ref(), IdealSolnGasVPSS::gibbs_mole(), IdealSolidSolnPhase::gibbs_mole(), IdealGasPhase::gibbs_mole(), IdealSolidSolnPhase::intEnergy_mole(), IdealGasPhase::intEnergy_mole(), IdealGasPhase::logStandardConc(), IdealGasPhase::pressure(), ThermoPhase::report(), PureFluidPhase::report(), MolalityVPSSTP::report(), HMWSoln::s_updatePitzer_CoeffWRTemp(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_lnMolalityActCoeff(), WaterSSTP::satPressure(), HMWSoln::satPressure(), Phase::saveState(), WaterSSTP::setDensity(), ThermoPhase::setElementPotentials(), WaterSSTP::setPressure(), VPStandardStateTP::setPressure(), IdealMolalSoln::setPressure(), IdealGasPhase::setPressure(), DebyeHuckel::setPressure(), SingleSpeciesTP::setState_HP(), ThermoPhase::setState_HPorUV(), SingleSpeciesTP::setState_SP(), ThermoPhase::setState_SPorSV(), SingleSpeciesTP::setState_SV(), SingleSpeciesTP::setState_UV(), IdealSolnGasVPSS::standardConcentration(), IdealGasPhase::standardConcentration(), MetalSHEelectrons::thermalExpansionCoeff(), IdealGasPhase::thermalExpansionCoeff(), VPStandardStateTP::updateStandardStateThermo(), and WaterSSTP::vaporFraction().
| doublereal thermalExpansionCoeff | ( | ) | const [virtual] |
The thermal expansion coefficient.
Units: 1/K. The thermal expansion coefficient is defined as
![\[ \beta = \frac{1}{v}\left(\frac{\partial v}{\partial T}\right)_P \]](form_96.png)
Reimplemented from ThermoPhase.
Definition at line 802 of file HMWSoln.cpp.
| virtual void updateDensity | ( | ) | [inline, virtual, inherited] |
| void updateStandardStateThermo | ( | ) | const [virtual, inherited] |
Updates the standard state thermodynamic functions at the current T and P of the solution.
If m_useTmpStandardStateStorage is true, this function must be called for every call to functions in this class. It checks to see whether the temperature or pressure has changed and thus the ss thermodynamics functions for all of the species must be recalculated.
This function is responsible for updating the following internal members, when m_useTmpStandardStateStorage is true.
- m_hss_RT;
- m_cpss_R;
- m_gss_RT;
- m_sss_R;
- m_Vss
If m_useTmpStandardStateStorage is not true, this function may be required to be called by child classes to update internal member data.
Definition at line 501 of file VPStandardStateTP.cpp.
References VPStandardStateTP::_updateStandardStateThermo(), VPStandardStateTP::m_Pcurrent, VPStandardStateTP::m_Plast_ss, VPStandardStateTP::m_Tlast_ss, and State::temperature().
Referenced by IdealSolnGasVPSS::cp_mole(), IdealSolnGasVPSS::enthalpy_mole(), IdealSolnGasVPSS::entropy_mole(), HMWSoln::getActivities(), VPStandardStateTP::getCp_R(), VPStandardStateTP::getCp_R_ref(), VPStandardStateTP::getEnthalpy_RT(), VPStandardStateTP::getEnthalpy_RT_ref(), VPStandardStateTP::getEntropy_R(), VPStandardStateTP::getEntropy_R_ref(), VPStandardStateTP::getGibbs_ref(), VPStandardStateTP::getGibbs_RT(), VPStandardStateTP::getGibbs_RT_ref(), VPStandardStateTP::getIntEnergy_RT(), VPStandardStateTP::getPureGibbs(), VPStandardStateTP::getStandardVolumes(), VPStandardStateTP::getStandardVolumes_ref(), HMWSoln::getUnscaledMolalityActivityCoefficients(), VPStandardStateTP::setPressure(), IdealSolnGasVPSS::setPressure(), VPStandardStateTP::setState_TP(), IdealMolalSoln::setState_TP(), VPStandardStateTP::setTemperature(), MolalityVPSSTP::setToEquilState(), IdealSolnGasVPSS::setToEquilState(), and HMWSoln::setToEquilState().
| virtual doublereal vaporFraction | ( | ) | const [inline, virtual] |
Return the fraction of vapor at the current conditions.
Reimplemented from ThermoPhase.
Definition at line 2037 of file HMWSoln.h.
References HMWSoln::err().
| XML_Node & xml | ( | ) | [inherited] |
Returns a reference to the XML_Node storred for the phase.
The XML_Node for the phase contains all of the input data used to set up the model for the phase, during its initialization.
Definition at line 112 of file Phase.cpp.
References Phase::m_xml.
Referenced by WaterSSTP::constructPhaseFile(), IdealSolidSolnPhase::constructPhaseFile(), IdealMolalSoln::constructPhaseFile(), HMWSoln::constructPhaseFile(), DebyeHuckel::constructPhaseFile(), and ThermoPhase::initThermoFile().
Member Data Documentation
doublereal CROP_ln_gamma_k_max [private] |
Parameter in the Molality Exp cutoff treatment.
Definition at line 3322 of file HMWSoln.h.
Referenced by HMWSoln::operator=(), and HMWSoln::readXMLCroppingCoefficients().
doublereal CROP_ln_gamma_k_min [private] |
Parameter in the Molality Exp cutoff treatment.
Definition at line 3319 of file HMWSoln.h.
Referenced by HMWSoln::operator=(), and HMWSoln::readXMLCroppingCoefficients().
doublereal CROP_ln_gamma_o_max [private] |
Parameter in the Molality Exp cutoff treatment.
Definition at line 3316 of file HMWSoln.h.
Referenced by HMWSoln::operator=(), and HMWSoln::readXMLCroppingCoefficients().
doublereal CROP_ln_gamma_o_min [private] |
Parameter in the Molality Exp cutoff treatment.
Definition at line 3313 of file HMWSoln.h.
Referenced by HMWSoln::operator=(), and HMWSoln::readXMLCroppingCoefficients().
std::vector<int> CROP_speciesCropped_ [mutable, private] |
This is a boolean-type vector indicating whether a species's activity coefficient is in the cropped regime.
0 = Not in cropped regime 1 = In a transition regime where it is altered but there still may be a temperature or pressure dependence 2 = In a cropped regime where there is no temperature or pressure dependence
Definition at line 3334 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_update_dlnMolalityActCoeff_dP(), and HMWSoln::s_update_dlnMolalityActCoeff_dT().
double elambda[17] [mutable, private] |
This is elambda, MEC.
Definition at line 3025 of file HMWSoln.h.
Referenced by HMWSoln::calc_lambdas(), HMWSoln::calc_thetas(), and HMWSoln::HMWSoln().
double elambda1[17] [mutable, private] |
This is elambda1, MEC.
Definition at line 3030 of file HMWSoln.h.
Referenced by HMWSoln::calc_lambdas(), HMWSoln::calc_thetas(), and HMWSoln::HMWSoln().
doublereal IMS_afCut_ [private] |
Parameter in the polyExp cutoff treatment having to do with rate of exp decay.
Definition at line 3258 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_agCut_ [private] |
Parameter in the polyExp cutoff treatment having to do with rate of exp decay.
Definition at line 3278 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_bfCut_ [private] |
Parameter in the polyExp cutoff treatment having to do with rate of exp decay.
Definition at line 3261 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_bgCut_ [private] |
Parameter in the polyExp cutoff treatment having to do with rate of exp decay.
Definition at line 3281 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_cCut_ [private] |
Parameter in the polyExp cutoff treatment having to do with rate of exp decay.
Definition at line 3242 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_dfCut_ [private] |
Parameter in the polyExp cutoff treatment having to do with rate of exp decay.
Definition at line 3252 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_dgCut_ [private] |
Parameter in the polyExp cutoff treatment having to do with rate of exp decay.
Definition at line 3272 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_efCut_ [private] |
Parameter in the polyExp cutoff treatment having to do with rate of exp decay.
Definition at line 3255 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_egCut_ [private] |
Parameter in the polyExp cutoff treatment having to do with rate of exp decay.
Definition at line 3275 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_gamma_k_min_ [private] |
gamma_k minimun for the cutoff process at the zero solvent point
Definition at line 3239 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_gamma_o_min_ [private] |
gamma_o value for the cutoff process at the zero solvent point
Definition at line 3236 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
vector_fp IMS_lnActCoeffMolal_ [mutable, private] |
Logarithm of the molal activity coefficients.
Normally these are all one. However, stability schemes will change that
Definition at line 3226 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_slopefCut_ [private] |
Parameter in the polyExp cutoff treatment.
This is the slope of the f function at the zero solvent point Default value is 0.6
Definition at line 3249 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), and HMWSoln::operator=().
doublereal IMS_slopegCut_ [private] |
Parameter in the polyExp cutoff treatment.
This is the slope of the g function at the zero solvent point Default value is 0.0
Definition at line 3268 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), and HMWSoln::operator=().
int IMS_typeCutoff_ [private] |
IMS Cutoff type.
Definition at line 3229 of file HMWSoln.h.
Referenced by HMWSoln::initThermoXML(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
doublereal IMS_X_o_cutoff_ [private] |
value of the solute mole fraction that centers the cutoff polynomials for the cutoff =1 process;
Definition at line 3233 of file HMWSoln.h.
Referenced by HMWSoln::calcIMSCutoffParams_(), HMWSoln::operator=(), and HMWSoln::s_updateIMS_lnMolalityActCoeff().
double m_A_Debye [mutable, private] |
A_Debye -> this expression appears on the top of the ln actCoeff term in the general Debye-Huckel expression It depends on temperature.
And, therefore, most be recalculated whenever T or P changes. This variable is a local copy of the calculation.
A_Debye = (F e B_Debye) / (8 Pi epsilon R T)
where B_Debye = F / sqrt(epsilon R T/2) (dw/1000)^(1/2)
A_Debye = (1/ (8 Pi)) (2 Na * dw/1000)^(1/2) (e * e / (epsilon * kb * T))^(3/2)
Units = sqrt(kg/gmol)
Nominal value = 1.172576 sqrt(kg/gmol) based on: epsilon/epsilon_0 = 78.54 (water at 25C) epsilon_0 = 8.854187817E-12 C2 N-1 m-2 e = 1.60217653 E-19 C F = 9.6485309E7 C kmol-1 R = 8.314472E3 kg m2 s-2 kmol-1 K-1 T = 298.15 K B_Debye = 3.28640E9 sqrt(kg/gmol)/m dw = C_0 * M_0 (density of water) (kg/m3) = 1.0E3 at 25C
Definition at line 2535 of file HMWSoln.h.
Referenced by HMWSoln::A_Debye_TP(), HMWSoln::initThermoXML(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
array_fp m_Aionic [private] |
Species molar volumes 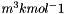 -> m_speciesSize in Constituents.h.
-> m_speciesSize in Constituents.h.
a_k = Size of the ionic species in the DH formulation units = meters
Definition at line 2455 of file HMWSoln.h.
Referenced by HMWSoln::AionicRadius(), HMWSoln::initLengths(), HMWSoln::initThermoXML(), and HMWSoln::operator=().
vector_fp m_Alpha1MX_ij [private] |
Array of 2D data used in the Pitzer/HMW formulation.
Alpha1MX_ij[i][j] is the value of the alpha1 coefficient for the ij interaction. It will be nonzero iff i and j are both charged and have opposite sign. It is symmetric wrt i, j. counterIJ where counterIJ = m_counterIJ[i][j] is used to access this array.
Definition at line 2712 of file HMWSoln.h.
Referenced by HMWSoln::HMWSoln(), HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_Alpha2MX_ij [private] |
Array of 2D data used in the Pitzer/HMW formulation.
Alpha2MX_ij[i][j] is the value of the alpha2 coefficient for the ij interaction. It will be nonzero iff i and j are both charged and have opposite sign, and i and j both have charges of 2 or more, usually. It is symmetric wrt i, j. counterIJ, where counterIJ = m_counterIJ[i][j], is used to access this array.
Definition at line 2724 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_Beta0MX_ij [mutable, private] |
Array of 2D data used in the Pitzer/HMW formulation.
Beta0_ij[i][j] is the value of the Beta0 coefficient for the ij salt. It will be nonzero iff i and j are both charged and have opposite sign. The array is also symmetric. counterIJ where counterIJ = m_counterIJ[i][j] is used to access this array.
Definition at line 2598 of file HMWSoln.h.
Referenced by HMWSoln::HMWSoln(), HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
Array2D m_Beta0MX_ij_coeff [mutable, private] |
Array of coefficients for Beta0, a variable in Pitzer's papers.
column index is counterIJ m_Beta0MX_ij_coeff.ptrColumn(counterIJ) is a double* containing the vector of coefficients for the counterIJ interaction.
Definition at line 2624 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), and HMWSoln::s_updatePitzer_CoeffWRTemp().
vector_fp m_Beta0MX_ij_L [mutable, private] |
Derivative of Beta0_ij[i][j] wrt T.
vector index is counterIJ
Definition at line 2604 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_Beta0MX_ij_LL [mutable, private] |
Derivative of Beta0_ij[i][j] wrt TT.
vector index is counterIJ
Definition at line 2610 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_Beta0MX_ij_P [mutable, private] |
Derivative of Beta0_ij[i][j] wrt P.
vector index is counterIJ
Definition at line 2616 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
vector_fp m_Beta1MX_ij [mutable, private] |
Array of 2D data used in the Pitzer/HMW formulation. Beta1_ij[i][j] is the value of the Beta1 coefficient for the ij salt. It will be nonzero iff i and j are both charged and have opposite sign. The array is also symmetric. counterIJ where counterIJ = m_counterIJ[i][j] is used to access this array.
Definition at line 2635 of file HMWSoln.h.
Referenced by HMWSoln::HMWSoln(), HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
Array2D m_Beta1MX_ij_coeff [mutable, private] |
Array of coefficients for Beta1, a variable in Pitzer's papers.
column index is counterIJ m_Beta1MX_ij_coeff.ptrColumn(counterIJ) is a double* containing the vector of coefficients for the counterIJ interaction.
Definition at line 2661 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), and HMWSoln::s_updatePitzer_CoeffWRTemp().
vector_fp m_Beta1MX_ij_L [mutable, private] |
Derivative of Beta1_ij[i][j] wrt T.
vector index is counterIJ
Definition at line 2641 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_Beta1MX_ij_LL [mutable, private] |
Derivative of Beta1_ij[i][j] wrt TT.
vector index is counterIJ
Definition at line 2647 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_Beta1MX_ij_P [mutable, private] |
Derivative of Beta1_ij[i][j] wrt P.
vector index is counterIJ
Definition at line 2653 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
vector_fp m_Beta2MX_ij [mutable, private] |
Array of 2D data used in the Pitzer/HMW formulation.
Beta2_ij[i][j] is the value of the Beta2 coefficient for the ij salt. It will be nonzero iff i and j are both charged and have opposite sign, and i and j both have charges of 2 or more. The array is also symmetric. counterIJ where counterIJ = m_counterIJ[i][j] is used to access this array.
Definition at line 2673 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
Array2D m_Beta2MX_ij_coeff [mutable, private] |
Array of coefficients for Beta2, a variable in Pitzer's papers.
column index is counterIJ m_Beta2MX_ij_coeff.ptrColumn(counterIJ) is a double* containing the vector of coefficients for the counterIJ interaction. This was added for the YMP database version of the code since it contains temperature-dependent parameters for some 2-2 electrolytes.
Definition at line 2701 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), and HMWSoln::s_updatePitzer_CoeffWRTemp().
vector_fp m_Beta2MX_ij_L [mutable, private] |
Derivative of Beta2_ij[i][j] wrt T.
vector index is counterIJ
Definition at line 2679 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_Beta2MX_ij_LL [mutable, private] |
Derivative of Beta2_ij[i][j] wrt TT.
vector index is counterIJ
Definition at line 2685 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_Beta2MX_ij_P [mutable, private] |
Derivative of Beta2_ij[i][j] wrt P.
vector index is counterIJ
Definition at line 2691 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
vector_fp m_BMX_IJ [mutable, private] |
Intermediate variable called BMX in Pitzer's paper This is the basic cation - anion interaction.
vector index is counterIJ
Definition at line 3070 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_BMX_IJ_L [mutable, private] |
Derivative of BMX_IJ wrt T.
vector index is counterIJ
Definition at line 3076 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_BMX_IJ_LL [mutable, private] |
Derivative of BMX_IJ wrt TT.
vector index is counterIJ
Definition at line 3082 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_BMX_IJ_P [mutable, private] |
Derivative of BMX_IJ wrt P.
vector index is counterIJ
Definition at line 3088 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
vector_fp m_BphiMX_IJ [mutable, private] |
Intermediate variable called BphiMX in Pitzer's paper.
vector index is counterIJ
Definition at line 3118 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_BphiMX_IJ_L [mutable, private] |
Derivative of BphiMX_IJ wrt T.
vector index is counterIJ
Definition at line 3124 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_BphiMX_IJ_LL [mutable, private] |
Derivative of BphiMX_IJ wrt TT.
vector index is counterIJ
Definition at line 3130 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_BphiMX_IJ_P [mutable, private] |
Derivative of BphiMX_IJ wrt P.
vector index is counterIJ
Definition at line 3136 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
vector_fp m_BprimeMX_IJ [mutable, private] |
Intermediate variable called BprimeMX in Pitzer's paper.
vector index is counterIJ
Definition at line 3094 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_BprimeMX_IJ_L [mutable, private] |
Derivative of BprimeMX wrt T.
vector index is counterIJ
Definition at line 3100 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_BprimeMX_IJ_LL [mutable, private] |
Derivative of BprimeMX wrt TT.
vector index is counterIJ
Definition at line 3106 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_BprimeMX_IJ_P [mutable, private] |
Derivative of BprimeMX wrt P.
vector index is counterIJ
Definition at line 3112 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
bool m_chargeNeutralityNecessary [protected, inherited] |
Boolean indicating whether a charge neutrality condition is a necessity.
Note, the charge neutrality condition is not a necessity for ideal gas phases. There may be a net charge in those phases, because the NASA polynomials for ionized species in Ideal gases take this condition into account. However, liquid phases usually require charge neutrality in order for their derived thermodynamics to be valid.
Definition at line 2130 of file ThermoPhase.h.
Referenced by ThermoPhase::chargeNeutralityNecessary(), MolalityVPSSTP::MolalityVPSSTP(), and ThermoPhase::operator=().
vector_fp m_CMX_IJ [mutable, private] |
Intermediate variable called CMX in Pitzer's paper.
vector index is counterIJ
Definition at line 3196 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_CMX_IJ_L [mutable, private] |
Derivative of m_CMX_IJ wrt T.
vector index is counterIJ
Definition at line 3202 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_CMX_IJ_LL [mutable, private] |
Derivative of m_CMX_IJ wrt TT.
vector index is counterIJ
Definition at line 3208 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_CMX_IJ_P [mutable, private] |
Derivative of m_CMX_IJ wrt P.
vector index is counterIJ
Definition at line 3214 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
array_int m_CounterIJ [mutable, private] |
a counter variable for keeping track of symmetric binary interactions amongst the solute species.
n = m_kk*i + j m_CounterIJ[n] = counterIJ
Definition at line 3020 of file HMWSoln.h.
Referenced by HMWSoln::counterIJ_setup(), HMWSoln::HMWSoln(), HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), HMWSoln::readXMLPsiCommonAnion(), HMWSoln::readXMLPsiCommonCation(), HMWSoln::readXMLThetaAnion(), HMWSoln::readXMLThetaCation(), HMWSoln::s_updatePitzer_CoeffWRTemp(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_CphiMX_ij [mutable, private] |
Array of 2D data used in the Pitzer/HMW formulation.
CphiMX_ij[i][j] is the value of the Cphi coefficient for the ij interaction. It will be nonzero iff i and j are both charged and have opposite sign, and i and j both have charges of 2 or more. The array is also symmetric. counterIJ where counterIJ = m_counterIJ[i][j] is used to access this array.
Definition at line 2736 of file HMWSoln.h.
Referenced by HMWSoln::HMWSoln(), HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
Array2D m_CphiMX_ij_coeff [mutable, private] |
Array of coefficients for CphiMX, a parameter in the activity coefficient formulation.
Column index is counterIJ m_CphiMX_ij_coeff.ptrColumn(counterIJ) is a double* containing the vector of coefficients for the counterIJ interaction.
Definition at line 2763 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), and HMWSoln::s_updatePitzer_CoeffWRTemp().
vector_fp m_CphiMX_ij_L [mutable, private] |
Derivative of Cphi_ij[i][j] wrt T.
vector index is counterIJ
Definition at line 2742 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_CphiMX_ij_LL [mutable, private] |
Derivative of Cphi_ij[i][j] wrt TT.
vector index is counterIJ
Definition at line 2748 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_CphiMX_ij_P [mutable, private] |
Derivative of Cphi_ij[i][j] wrt P.
vector index is counterIJ
Definition at line 2754 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
vector_fp m_d2lnActCoeffMolaldT2_Scaled [mutable, private] |
Derivative of the Logarithm of the activity coefficients on the molality scale wrt TT.
index is the species index
Definition at line 2980 of file HMWSoln.h.
Referenced by HMWSoln::getPartialMolarCp(), HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updateScaling_pHScaling_dT2().
vector_fp m_d2lnActCoeffMolaldT2_Unscaled [mutable, private] |
Derivative of the Logarithm of the activity coefficients on the molality.
scale wrt TT
index is the species index
Definition at line 2987 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), and HMWSoln::s_updateScaling_pHScaling_dT2().
int m_debugCalc [mutable] |
Turn on copious debug printing when this is true and DEBUG_MODE is turned on.
Definition at line 3611 of file HMWSoln.h.
Referenced by HMWSoln::calc_lambdas(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
double m_densWaterSS [private] |
density of standard-state water
internal temporary variable
Definition at line 2547 of file HMWSoln.h.
Referenced by HMWSoln::operator=().
vector_fp m_dlnActCoeffMolaldP_Scaled [mutable, private] |
Derivative of the Logarithm of the activity coefficients on the molality scale wrt P.
index is the species index
Definition at line 2994 of file HMWSoln.h.
Referenced by HMWSoln::getPartialMolarVolumes(), HMWSoln::initLengths(), and HMWSoln::operator=().
vector_fp m_dlnActCoeffMolaldP_Unscaled [mutable, private] |
Derivative of the Logarithm of the activity coefficients on the molality scale wrt P.
index is the species index
Definition at line 3001 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_update_dlnMolalityActCoeff_dP(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
vector_fp m_dlnActCoeffMolaldT_Scaled [mutable, private] |
Derivative of the Logarithm of the activity coefficients on the molality scale wrt T.
index is the species index
Definition at line 2966 of file HMWSoln.h.
Referenced by HMWSoln::getPartialMolarCp(), HMWSoln::getPartialMolarEnthalpies(), HMWSoln::getPartialMolarEntropies(), HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updateScaling_pHScaling_dT().
vector_fp m_dlnActCoeffMolaldT_Unscaled [mutable, private] |
Derivative of the Logarithm of the activity coefficients on the molality scale wrt T.
index is the species index
Definition at line 2973 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_update_dlnMolalityActCoeff_dT(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updateScaling_pHScaling_dT().
vector_int m_electrolyteSpeciesType [private] |
Vector containing the electrolyte species type.
The possible types are:
- solvent
- Charged Species
- weakAcidAssociated
- strongAcidAssociated
- polarNeutral
- nonpolarNeutral .
Definition at line 2443 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), and HMWSoln::initThermoXML().
Elements* m_Elements [protected, inherited] |
Pointer to the element object corresponding to this phase. Normally, this will be the default Element object common to all phases.
Definition at line 366 of file Constituents.h.
Referenced by Constituents::addElement(), Constituents::addElementsFromXML(), Constituents::addUniqueElement(), Constituents::addUniqueSpecies(), Constituents::atomicNumber(), Constituents::atomicWeight(), Constituents::atomicWeights(), Constituents::Constituents(), Constituents::elementIndex(), Constituents::elementName(), Constituents::elementNames(), Constituents::elementsFrozen(), Constituents::entropyElement298(), Constituents::freezeElements(), Constituents::getAtoms(), Constituents::nAtoms(), Constituents::nElements(), Constituents::operator=(), Constituents::ready(), and Constituents::~Constituents().
vector_fp m_expg0_RT [mutable, private] |
Vector containing the species reference exp(-G/RT) functions at T = m_tlast.
Definition at line 2558 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), and HMWSoln::operator=().
| int m_form_A_Debye |
Form of the constant outside the Debye-Huckel term called A.
It's normally a function of temperature and pressure. However, it can be set from the input file in order to aid in numerical comparisons. Acceptable forms:
A_DEBYE_CONST 0 A_DEBYE_WATER 1
The A_DEBYE_WATER form may be used for water solvents with needs to cover varying temperatures and pressures. Note, the dielectric constant of water is a relatively strong function of T, and its variability must be accounted for,
Definition at line 2501 of file HMWSoln.h.
Referenced by HMWSoln::A_Debye_TP(), HMWSoln::d2A_DebyedT2_TP(), HMWSoln::dA_DebyedP_TP(), HMWSoln::dA_DebyedT_TP(), HMWSoln::initThermoXML(), and HMWSoln::operator=().
int m_formGC [private] |
Format for the generalized concentration:
0 = unity 1 = molar_volume 2 = solvent_volume (default)
The generalized concentrations can have three different forms depending on the value of the member attribute m_formGC, which is supplied in the constructor.
| m_formGC | GeneralizedConc | StandardConc |
| 0 | X_k | 1.0 |
| 1 | X_k / V_k | 1.0 / V_k |
| 2 | X_k / V_N | 1.0 / V_N |
The value and form of the generalized concentration will affect reaction rate constants involving species in this phase.
(HKM Note: Using option #1 may lead to spurious results and has been included only with warnings. The reason is that it molar volumes of electrolytes may often be negative. The molar volume of H+ is defined to be zero too. Either options 0 or 2 are the appropriate choice. Option 0 leads to bulk reaction rate constants which have units of s-1. Option 2 leads to bulk reaction rate constants for bimolecular rxns which have units of m-3 kmol-1 s-1.)
Definition at line 2431 of file HMWSoln.h.
Referenced by HMWSoln::constructPhaseXML(), HMWSoln::eosType(), and HMWSoln::operator=().
int m_formPitzer [private] |
This is the form of the Pitzer parameterization used in this model.
The options are described at the top of this document, and in the general documentation. The list is repeated here:
PITZERFORM_BASE = 0 (only one supported atm)
Definition at line 2390 of file HMWSoln.h.
Referenced by HMWSoln::constructPhaseXML(), HMWSoln::formPitzer(), and HMWSoln::operator=().
int m_formPitzerTemp [private] |
This is the form of the temperature dependence of Pitzer parameterization used in the model.
PITZER_TEMP_CONSTANT 0 PITZER_TEMP_LINEAR 1 PITZER_TEMP_COMPLEX1 2
Definition at line 2400 of file HMWSoln.h.
Referenced by HMWSoln::constructPhaseXML(), HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLBinarySalt(), HMWSoln::readXMLLambdaNeutral(), HMWSoln::readXMLMunnnNeutral(), HMWSoln::readXMLPsiCommonAnion(), HMWSoln::readXMLPsiCommonCation(), HMWSoln::readXMLThetaAnion(), HMWSoln::readXMLThetaCation(), HMWSoln::readXMLZetaCation(), and HMWSoln::s_updatePitzer_CoeffWRTemp().
vector_fp m_g2func_IJ [mutable, private] |
This is the value of g2(x2) in Pitzer's papers.
vector index is counterIJ
Definition at line 3049 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_gamma_tmp [mutable, private] |
Intermediate storage of the activity coefficient itself.
vector index is the species index
Definition at line 3220 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_gfunc_IJ [mutable, private] |
Various temporary arrays used in the calculation of the Pitzer activity coefficents.
The subscript, L, denotes the same quantity's derivative wrt temperature This is the value of g(x) in Pitzer's papers
vector index is counterIJ
Definition at line 3043 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_h2func_IJ [mutable, private] |
hfunc2, was called gprime in Pitzer's paper.
However, it's not the derivative of gfunc(x), so I renamed it.
vector index is counterIJ
Definition at line 3063 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
bool m_hasElementPotentials [protected, inherited] |
Boolean indicating whether there is a valid set of saved element potentials for this phase.
Definition at line 2120 of file ThermoPhase.h.
Referenced by ThermoPhase::getElementPotentials(), ThermoPhase::operator=(), and ThermoPhase::setElementPotentials().
vector_fp m_hfunc_IJ [mutable, private] |
hfunc, was called gprime in Pitzer's paper.
However, it's not the derivative of gfunc(x), so I renamed it.
vector index is counterIJ
Definition at line 3056 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
double m_IionicMolality [mutable, private] |
Current value of the ionic strength on the molality scale Associated Salts, if present in the mechanism, don't contribute to the value of the ionic strength in this version of the Ionic strength.
Definition at line 2463 of file HMWSoln.h.
Referenced by HMWSoln::debugPrinting(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
double m_IionicMolalityStoich [mutable, private] |
Stoichiometric ionic strength on the molality scale.
This differs from m_IionicMolality in the sense that associated salts are treated as unassociated salts, when calculating the Ionic strength by this method.
Definition at line 2482 of file HMWSoln.h.
Referenced by HMWSoln::operator=().
int m_index [protected, inherited] |
Index number of the phase.
The Cantera interface library uses this member to set the index number to the location of the pointer to this object in the pointer array of ThermoPhase's it maintains. Using this member for any other purpose will lead to unpredictable results if used in conjunction with the interface library.
Reimplemented from Phase.
Definition at line 2106 of file ThermoPhase.h.
Referenced by ThermoPhase::index(), ThermoPhase::operator=(), and ThermoPhase::setIndex().
int m_indexCLM [protected, inherited] |
Index of the phScale species.
Index of the species to be used in the single-ion scaling law. This is the indentity of the Cl- species for the PHSCALE_NBS scaling
Definition at line 872 of file MolalityVPSSTP.h.
Referenced by HMWSoln::applyphScale(), MolalityVPSSTP::initThermo(), MolalityVPSSTP::operator=(), HMWSoln::s_updateScaling_pHScaling(), HMWSoln::s_updateScaling_pHScaling_dT(), and HMWSoln::s_updateScaling_pHScaling_dT2().
int m_indexSolvent [protected, inherited] |
Index of the solvent.
Currently the index of the solvent is hard-coded to the value 0
Definition at line 854 of file MolalityVPSSTP.h.
Referenced by DebyeHuckel::_lnactivityWaterHelgesonFixedForm(), MolalityVPSSTP::calcMolalities(), IdealMolalSoln::getActivities(), HMWSoln::getActivities(), DebyeHuckel::getActivities(), MolalityVPSSTP::getActivityCoefficients(), IdealMolalSoln::getChemPotentials(), HMWSoln::getChemPotentials(), DebyeHuckel::getChemPotentials(), IdealMolalSoln::getMolalityActivityCoefficients(), IdealMolalSoln::getPartialMolarEntropies(), HMWSoln::getPartialMolarEntropies(), DebyeHuckel::getPartialMolarEntropies(), IdealMolalSoln::initThermoXML(), HMWSoln::initThermoXML(), DebyeHuckel::initThermoXML(), MolalityVPSSTP::operator=(), MolalityVPSSTP::osmoticCoefficient(), DebyeHuckel::s_update_d2lnMolalityActCoeff_dT2(), DebyeHuckel::s_update_dlnMolalityActCoeff_dP(), DebyeHuckel::s_update_dlnMolalityActCoeff_dT(), DebyeHuckel::s_update_lnMolalityActCoeff(), IdealMolalSoln::s_updateIMS_lnMolalityActCoeff(), HMWSoln::s_updateIMS_lnMolalityActCoeff(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), HMWSoln::s_updatePitzer_lnMolalityActCoeff(), MolalityVPSSTP::setMolalities(), MolalityVPSSTP::setMolalitiesByName(), MolalityVPSSTP::setSolvent(), MolalityVPSSTP::solventIndex(), IdealMolalSoln::standardConcentration(), HMWSoln::standardConcentration(), and DebyeHuckel::standardConcentration().
int m_kk [protected, inherited] |
m_kk = Number of species in the phase.
For internal use only.
m_kk is a member of both the State and Constituents classes. Therefore, to avoid multiple inheritance problems, we need to restate it in here, so that the declarations in the two base classes become hidden.
Reimplemented from Constituents.
Definition at line 504 of file Phase.h.
Referenced by DebyeHuckel::_lnactivityWaterHelgesonFixedForm(), SurfPhase::_updateThermo(), IdealSolidSolnPhase::_updateThermo(), IdealGasPhase::_updateThermo(), IdealMolalSoln::calcDensity(), DebyeHuckel::calcDensity(), MolalityVPSSTP::calcMolalities(), ConstDensityThermo::expGibbs_RT(), IdealSolidSolnPhase::expGibbs_RT_ref(), IdealGasPhase::expGibbs_RT_ref(), MolalityVPSSTP::findCLMIndex(), Phase::freezeSpecies(), IdealMolalSoln::getActivities(), DebyeHuckel::getActivities(), ThermoPhase::getActivityCoefficients(), SingleSpeciesTP::getActivityCoefficients(), MolalityVPSSTP::getActivityCoefficients(), IdealSolnGasVPSS::getActivityCoefficients(), IdealSolidSolnPhase::getActivityCoefficients(), IdealGasPhase::getActivityCoefficients(), IdealSolnGasVPSS::getActivityConcentrations(), IdealSolidSolnPhase::getActivityConcentrations(), IdealMolalSoln::getActivityConcentrations(), DebyeHuckel::getActivityConcentrations(), SurfPhase::getChemPotentials(), IdealSolnGasVPSS::getChemPotentials(), IdealSolidSolnPhase::getChemPotentials(), IdealMolalSoln::getChemPotentials(), IdealGasPhase::getChemPotentials(), DebyeHuckel::getChemPotentials(), VPStandardStateTP::getChemPotentials_RT(), IdealSolnGasVPSS::getChemPotentials_RT(), IdealSolidSolnPhase::getChemPotentials_RT(), SurfPhase::getCoverages(), IdealSolidSolnPhase::getCp_R_ref(), ThermoPhase::getElectrochemPotentials(), MolalityVPSSTP::getElectrochemPotentials(), IdealSolidSolnPhase::getEnthalpy_RT(), IdealSolidSolnPhase::getEnthalpy_RT_ref(), IdealGasPhase::getEntropy_R(), IdealSolidSolnPhase::getEntropy_R_ref(), WaterSSTP::getGibbs_ref(), IdealSolidSolnPhase::getGibbs_ref(), IdealSolidSolnPhase::getGibbs_RT(), IdealGasPhase::getGibbs_RT(), IdealSolidSolnPhase::getGibbs_RT_ref(), IdealSolidSolnPhase::getIntEnergy_RT(), IdealGasPhase::getIntEnergy_RT(), IdealSolidSolnPhase::getIntEnergy_RT_ref(), IdealGasPhase::getIntEnergy_RT_ref(), MolalityVPSSTP::getMolalities(), IdealMolalSoln::getMolalityActivityCoefficients(), DebyeHuckel::getMolalityActivityCoefficients(), SurfPhase::getPartialMolarCp(), IdealSolnGasVPSS::getPartialMolarCp(), IdealSolidSolnPhase::getPartialMolarCp(), IdealMolalSoln::getPartialMolarCp(), DebyeHuckel::getPartialMolarCp(), SurfPhase::getPartialMolarEnthalpies(), IdealSolnGasVPSS::getPartialMolarEnthalpies(), IdealMolalSoln::getPartialMolarEnthalpies(), DebyeHuckel::getPartialMolarEnthalpies(), SurfPhase::getPartialMolarEntropies(), IdealSolnGasVPSS::getPartialMolarEntropies(), IdealSolidSolnPhase::getPartialMolarEntropies(), IdealMolalSoln::getPartialMolarEntropies(), IdealGasPhase::getPartialMolarEntropies(), DebyeHuckel::getPartialMolarEntropies(), IdealSolnGasVPSS::getPartialMolarIntEnergies(), IdealGasPhase::getPartialMolarIntEnergies(), IdealGasPhase::getPartialMolarVolumes(), DebyeHuckel::getPartialMolarVolumes(), IdealSolidSolnPhase::getPureGibbs(), IdealGasPhase::getPureGibbs(), ThermoPhase::getReferenceComposition(), VPStandardStateTP::getStandardChemPotentials(), IdealGasPhase::getStandardChemPotentials(), SurfPhase::getStandardVolumes(), IdealGasPhase::getStandardVolumes(), IdealGasPhase::getStandardVolumes_ref(), HMWSoln::HMWSoln(), VPStandardStateTP::initLengths(), MolalityVPSSTP::initLengths(), IdealSolnGasVPSS::initLengths(), IdealSolidSolnPhase::initLengths(), IdealMolalSoln::initLengths(), DebyeHuckel::initLengths(), VPStandardStateTP::initThermo(), ThermoPhase::initThermo(), SurfPhase::initThermo(), StoichSubstanceSSTP::initThermo(), SingleSpeciesTP::initThermo(), IdealGasPhase::initThermo(), VPStandardStateTP::initThermoXML(), IdealSolidSolnPhase::initThermoXML(), IdealMolalSoln::initThermoXML(), HMWSoln::initThermoXML(), DebyeHuckel::initThermoXML(), IdealSolidSolnPhase::logStandardConc(), VPStandardStateTP::operator=(), ThermoPhase::operator=(), Phase::operator=(), MolalityVPSSTP::osmoticCoefficient(), HMWSoln::readXMLBinarySalt(), HMWSoln::readXMLLambdaNeutral(), HMWSoln::readXMLPsiCommonAnion(), HMWSoln::readXMLPsiCommonCation(), HMWSoln::readXMLThetaAnion(), HMWSoln::readXMLThetaCation(), HMWSoln::readXMLZetaCation(), Phase::ready(), IdealSolidSolnPhase::referenceConcentration(), DebyeHuckel::s_update_d2lnMolalityActCoeff_dT2(), DebyeHuckel::s_update_dlnMolalityActCoeff_dP(), DebyeHuckel::s_update_dlnMolalityActCoeff_dT(), DebyeHuckel::s_update_lnMolalityActCoeff(), IdealMolalSoln::s_updateIMS_lnMolalityActCoeff(), SurfPhase::setCoverages(), SurfPhase::setCoveragesNoNorm(), MolalityVPSSTP::setMolalities(), ThermoPhase::setReferenceComposition(), MolalityVPSSTP::setSolvent(), IdealSolnGasVPSS::setToEquilState(), IdealSolidSolnPhase::setToEquilState(), IdealGasPhase::setToEquilState(), ThermoPhase::speciesData(), IdealSolidSolnPhase::standardConcentration(), and ThermoPhase::~ThermoPhase().
Array2D m_Lambda_nj [mutable, private] |
Lambda coefficient for the ij interaction.
Array of 2D data used in the Pitzer/HMW formulation. Lambda_nj[n][j] represents the lambda coefficient for the ij interaction. This is a general interaction representing neutral species. The neutral species occupy the first index, i.e., n. The charged species occupy the j coordinate. neutral, neutral interactions are also included here.
Definition at line 2868 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLLambdaNeutral(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
Array2D m_Lambda_nj_coeff [private] |
Array of coefficients for Lambda_nj[i][j] in the Pitzer/HMW formulation.
Lambda_ij[i][j] is the value of the theta coefficient for the ij interaction. Array of 2D data used in the Pitzer/HMW formulation. Lambda_ij[i][j] represents the lambda coefficient for the ij interaction. This is a general interaction representing neutral species. The neutral species occupy the first index, i.e., i. The charged species occupy the j coordinate. Neutral, neutral interactions are also included here.
n = j + m_kk * i
m_Lambda_ij_coeff.ptrColumn(n) is a double* containing the vector of coefficients for the (i,j) interaction.
Definition at line 2895 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLLambdaNeutral(), and HMWSoln::s_updatePitzer_CoeffWRTemp().
Array2D m_Lambda_nj_L [mutable, private] |
Derivative of Lambda_nj[i][j] wrt T. see m_Lambda_ij.
Definition at line 2871 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
Array2D m_Lambda_nj_LL [mutable, private] |
Derivative of Lambda_nj[i][j] wrt TT.
Definition at line 2874 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
Array2D m_Lambda_nj_P [mutable, private] |
Derivative of Lambda_nj[i][j] wrt P.
Definition at line 2877 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
vector_fp m_lambdaRRT [protected, inherited] |
Vector of element potentials.
-> length equal to number of elements
Definition at line 2116 of file ThermoPhase.h.
Referenced by ThermoPhase::getElementPotentials(), ThermoPhase::operator=(), and ThermoPhase::setElementPotentials().
vector_fp m_lnActCoeffMolal_Scaled [mutable, private] |
Logarithm of the activity coefficients on the molality scale.
mutable because we change this if the composition or temperature or pressure changes.
index is the species index
Definition at line 2949 of file HMWSoln.h.
Referenced by HMWSoln::getActivities(), HMWSoln::getChemPotentials(), HMWSoln::getPartialMolarEntropies(), HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updateScaling_pHScaling().
vector_fp m_lnActCoeffMolal_Unscaled [mutable, private] |
Logarithm of the activity coefficients on the molality.
scale.
mutable because we change this if the composition or temperature or pressure changes.
index is the species index
Definition at line 2959 of file HMWSoln.h.
Referenced by HMWSoln::applyphScale(), HMWSoln::getUnscaledMolalityActivityCoefficients(), HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_lnMolalityActCoeff(), and HMWSoln::s_updateScaling_pHScaling().
double m_maxIionicStrength [private] |
Maximum value of the ionic strength allowed in the calculation of the activity coefficients.
Definition at line 2469 of file HMWSoln.h.
Referenced by HMWSoln::initThermoXML(), and HMWSoln::operator=().
doublereal m_Mnaught [protected, inherited] |
This is the multiplication factor that goes inside log expressions involving the molalities of species.
Its equal to Wt_0 / 1000, where Wt_0 = weight of solvent (kg/kmol)
Definition at line 893 of file MolalityVPSSTP.h.
Referenced by DebyeHuckel::_lnactivityWaterHelgesonFixedForm(), MolalityVPSSTP::calcMolalities(), MolalityVPSSTP::operator=(), MolalityVPSSTP::osmoticCoefficient(), DebyeHuckel::s_update_d2lnMolalityActCoeff_dT2(), DebyeHuckel::s_update_dlnMolalityActCoeff_dP(), DebyeHuckel::s_update_dlnMolalityActCoeff_dT(), DebyeHuckel::s_update_lnMolalityActCoeff(), MolalityVPSSTP::setMolalities(), MolalityVPSSTP::setMolalitiesByName(), MolalityVPSSTP::setSolvent(), and HMWSoln::standardConcentration().
vector_fp m_molalities [mutable, protected, inherited] |
Current value of the molalities of the species in the phase.
Note this vector is a mutable quantity. units are (kg/kmol)
Definition at line 900 of file MolalityVPSSTP.h.
Referenced by DebyeHuckel::_lnactivityWaterHelgesonFixedForm(), MolalityVPSSTP::calcMolalities(), IdealMolalSoln::getActivities(), HMWSoln::getActivities(), DebyeHuckel::getActivities(), IdealMolalSoln::getChemPotentials(), HMWSoln::getChemPotentials(), DebyeHuckel::getChemPotentials(), MolalityVPSSTP::getMolalities(), IdealMolalSoln::getPartialMolarEntropies(), HMWSoln::getPartialMolarEntropies(), DebyeHuckel::getPartialMolarEntropies(), MolalityVPSSTP::initLengths(), MolalityVPSSTP::operator=(), MolalityVPSSTP::osmoticCoefficient(), DebyeHuckel::s_update_d2lnMolalityActCoeff_dT2(), DebyeHuckel::s_update_dlnMolalityActCoeff_dP(), DebyeHuckel::s_update_dlnMolalityActCoeff_dT(), DebyeHuckel::s_update_lnMolalityActCoeff(), HMWSoln::s_updatePitzer_lnMolalityActCoeff(), and MolalityVPSSTP::setMolalities().
bool m_molalitiesAreCropped [mutable, private] |
Boolean indicating whether the molalities are cropped or are modified.
Definition at line 3012 of file HMWSoln.h.
Referenced by HMWSoln::operator=().
vector_fp m_molalitiesCropped [mutable, private] |
Cropped and modified values of the molalities used in activity coefficient calculations.
Definition at line 3009 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_Mu_nnn [mutable, private] |
Mu coefficient for the self-ternary neutral coefficient.
Array of 2D data used in the Pitzer/HMW formulation. Mu_nnn[i] represents the Mu coefficient for the nnn interaction. This is a general interaction representing neutral species interacting with itself.
Definition at line 2905 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::readXMLMunnnNeutral(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
Array2D m_Mu_nnn_coeff [private] |
Array of coefficients form_Mu_nnn term.
Definition at line 2938 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::readXMLMunnnNeutral(), and HMWSoln::s_updatePitzer_CoeffWRTemp().
vector_fp m_Mu_nnn_L [mutable, private] |
Mu coefficient temperature derivative for the self-ternary neutral coefficient.
Array of 2D data used in the Pitzer/HMW formulation. Mu_nnn_L[i] represents the Mu coefficient temperature derivative for the nnn interaction. This is a general interaction representing neutral species interacting with itself.
Definition at line 2914 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_Mu_nnn_LL [mutable, private] |
Mu coefficient 2nd temperature derivative for the self-ternary neutral coefficient.
Array of 2D data used in the Pitzer/HMW formulation. Mu_nnn_L[i] represents the Mu coefficient 2nd temperature derivative for the nnn interaction. This is a general interaction representing neutral species interacting with itself.
Definition at line 2923 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_Mu_nnn_P [mutable, private] |
Mu coefficient pressure derivative for the self-ternary neutral coefficient.
Array of 2D data used in the Pitzer/HMW formulation. Mu_nnn_L[i] represents the Mu coefficient pressure derivative for the nnn interaction. This is a general interaction representing neutral species interacting with itself.
Definition at line 2932 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
int m_ndim [protected, inherited] |
m_ndim is the dimensionality of the phase.
Volumetric phases have dimensionality 3 and surface phases have dimensionality 2.
Definition at line 511 of file Phase.h.
Referenced by Phase::nDim(), Phase::operator=(), and Phase::setNDim().
doublereal m_P0 [protected, inherited] |
Reference pressure (Pa) must be the same for all species
- defaults to OneAtm
Definition at line 624 of file VPStandardStateTP.h.
Referenced by VPStandardStateTP::operator=().
doublereal m_Pcurrent [protected, inherited] |
Current value of the pressure - state variable.
Because we are now using the pressure as a state variable, we need to carry it along within this object
units = Pascals
Definition at line 611 of file VPStandardStateTP.h.
Referenced by VPStandardStateTP::_updateStandardStateThermo(), IdealSolnGasVPSS::calcDensity(), IdealSolnGasVPSS::isothermalCompressibility(), VPStandardStateTP::operator=(), VPStandardStateTP::pressure(), HMWSoln::pressure(), DebyeHuckel::pressure(), IdealSolnGasVPSS::setPressure(), VPStandardStateTP::setState_TP(), IdealMolalSoln::setState_TP(), DebyeHuckel::setState_TP(), VPStandardStateTP::setTemperature(), DebyeHuckel::setTemperature(), and VPStandardStateTP::updateStandardStateThermo().
std::vector<PDSS *> m_PDSS_storage [protected, inherited] |
Storage for the PDSS objects for the species.
Storage is in species index order. VPStandardStateTp owns each of the objects. Copy operations are deep.
Definition at line 639 of file VPStandardStateTP.h.
Referenced by VPStandardStateTP::initThermo(), VPStandardStateTP::initThermoXML(), VPStandardStateTP::operator=(), and VPStandardStateTP::~VPStandardStateTP().
vector_fp m_pe [mutable, private] |
Vector of potential energies for the species.
Definition at line 2563 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), and HMWSoln::operator=().
doublereal m_phi [protected, inherited] |
Storred value of the electric potential for this phase.
Units are Volts
Definition at line 2112 of file ThermoPhase.h.
Referenced by ThermoPhase::electricPotential(), IdealMolalSoln::electricPotential(), ThermoPhase::operator=(), ThermoPhase::setElectricPotential(), and IdealMolalSoln::setElectricPotential().
vector_fp m_Phi_IJ [mutable, private] |
Intermediate variable called Phi in Pitzer's paper.
vector index is counterIJ
Definition at line 3142 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_Phi_IJ_L [mutable, private] |
Derivative of m_Phi_IJ wrt T.
vector index is counterIJ
Definition at line 3148 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_Phi_IJ_LL [mutable, private] |
Derivative of m_Phi_IJ wrt TT.
vector index is counterIJ
Definition at line 3154 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_Phi_IJ_P [mutable, private] |
Derivative of m_Phi_IJ wrt P.
vector index is counterIJ
Definition at line 3160 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
vector_fp m_PhiPhi_IJ [mutable, private] |
Intermediate variable called PhiPhi in Pitzer's paper.
vector index is counterIJ
Definition at line 3172 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
vector_fp m_PhiPhi_IJ_L [mutable, private] |
Derivative of m_PhiPhi_IJ wrt T.
vector index is counterIJ
Definition at line 3178 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_PhiPhi_IJ_LL [mutable, private] |
Derivative of m_PhiPhi_IJ wrt TT.
vector index is counterIJ
Definition at line 3184 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_PhiPhi_IJ_P [mutable, private] |
Derivative of m_PhiPhi_IJ wrt P.
vector index is counterIJ
Definition at line 3190 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
vector_fp m_Phiprime_IJ [mutable, private] |
Intermediate variable called Phiprime in Pitzer's paper.
vector index is counterIJ
Definition at line 3166 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
int m_pHScalingType [protected, inherited] |
Scaling to be used for output of single-ion species activity coefficients.
Index of the species to be used in the single-ion scaling law. This is the indentity of the Cl- species for the PHSCALE_NBS scaling. Either PHSCALE_PITZER or PHSCALE_NBS
Definition at line 864 of file MolalityVPSSTP.h.
Referenced by HMWSoln::applyphScale(), MolalityVPSSTP::operator=(), MolalityVPSSTP::pHScale(), HMWSoln::s_updateScaling_pHScaling(), HMWSoln::s_updateScaling_pHScaling_dT(), HMWSoln::s_updateScaling_pHScaling_dT2(), and MolalityVPSSTP::setpHScale().
doublereal m_Plast_ss [mutable, protected, inherited] |
The last pressure at which the Standard State thermodynamic properties were calculated at.
Definition at line 618 of file VPStandardStateTP.h.
Referenced by VPStandardStateTP::_updateStandardStateThermo(), VPStandardStateTP::operator=(), and VPStandardStateTP::updateStandardStateThermo().
vector_fp m_pp [mutable, private] |
Temporary array used in equilibrium calculations.
Definition at line 2568 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::relative_enthalpy().
vector_fp m_Psi_ijk [mutable, private] |
Array of 3D data used in the Pitzer/HMW formulation.
Psi_ijk[n] is the value of the psi coefficient for the ijk interaction where
n = k + j * m_kk + i * m_kk * m_kk;
It is potentially nonzero everywhere. The first two coordinates are symmetric wrt cations, and the last two coordinates are symmetric wrt anions.
Definition at line 2822 of file HMWSoln.h.
Referenced by HMWSoln::HMWSoln(), HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLPsiCommonAnion(), HMWSoln::readXMLPsiCommonCation(), HMWSoln::readXMLZetaCation(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
Array2D m_Psi_ijk_coeff [private] |
Array of coefficients for Psi_ijk[n] in the Pitzer/HMW formulation.
Psi_ijk[n] is the value of the psi coefficient for the ijk interaction where
n = k + j * m_kk + i * m_kk * m_kk;
It is potentially nonzero everywhere. The first two coordinates are symmetric wrt cations, and the last two coordinates are symmetric wrt anions.
m_Psi_ijk_coeff.ptrColumn(n) is a double* containing the vector of coefficients for the n interaction.
Definition at line 2857 of file HMWSoln.h.
Referenced by HMWSoln::HMWSoln(), HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLPsiCommonAnion(), HMWSoln::readXMLPsiCommonCation(), HMWSoln::readXMLZetaCation(), and HMWSoln::s_updatePitzer_CoeffWRTemp().
vector_fp m_Psi_ijk_L [mutable, private] |
Derivitive of Psi_ijk[n] wrt T.
see m_Psi_ijk for reference on the indexing into this variable.
Definition at line 2828 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_Psi_ijk_LL [mutable, private] |
Derivitive of Psi_ijk[n] wrt TT.
see m_Psi_ijk for reference on the indexing into this variable.
Definition at line 2834 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_Psi_ijk_P [mutable, private] |
Derivitive of Psi_ijk[n] wrt P.
see m_Psi_ijk for reference on the indexing into this variable.
Definition at line 2840 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
vector_fp m_speciesCharge [protected, inherited] |
m_speciesCharge: Vector of species charges length = m_kk
Definition at line 383 of file Constituents.h.
Referenced by Constituents::addUniqueSpecies(), HMWSoln::applyphScale(), Constituents::charge(), HMWSoln::initThermoXML(), DebyeHuckel::initThermoXML(), Constituents::operator=(), HMWSoln::readXMLBinarySalt(), HMWSoln::readXMLLambdaNeutral(), HMWSoln::readXMLMunnnNeutral(), HMWSoln::readXMLPsiCommonAnion(), HMWSoln::readXMLPsiCommonCation(), HMWSoln::readXMLThetaAnion(), HMWSoln::readXMLThetaCation(), HMWSoln::readXMLZetaCation(), DebyeHuckel::s_update_d2lnMolalityActCoeff_dT2(), DebyeHuckel::s_update_dlnMolalityActCoeff_dP(), DebyeHuckel::s_update_dlnMolalityActCoeff_dT(), DebyeHuckel::s_update_lnMolalityActCoeff(), HMWSoln::s_updatePitzer_CoeffWRTemp(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), HMWSoln::s_updatePitzer_lnMolalityActCoeff(), HMWSoln::s_updateScaling_pHScaling(), HMWSoln::s_updateScaling_pHScaling_dT(), and HMWSoln::s_updateScaling_pHScaling_dT2().
vector_fp m_speciesCharge_Stoich [private] |
Stoichiometric species charge -> This is for calculations of the ionic strength which ignore ion-ion pairing into neutral molecules.
The Stoichiometric species charge is the charge of one of the ion that would occur if the species broke into two charged ion pairs. NaCl -> m_speciesCharge_Stoich = -1; HSO4- -> H+ + SO42- = -2 -> The other charge is calculated. For species that aren't ion pairs, its equal to the m_speciesCharge[] value.
Definition at line 2587 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::initThermoXML(), and HMWSoln::operator=().
vector_fp m_speciesComp [protected, inherited] |
Atomic composition of the species.
the number of atoms of i in species k is equal to m_speciesComp[k * m_mm + i] The length of this vector is equal to m_kk * m_mm
Definition at line 377 of file Constituents.h.
Referenced by Constituents::addUniqueSpecies(), Constituents::getAtoms(), Constituents::nAtoms(), and Constituents::operator=().
std::vector<const XML_Node *> m_speciesData [protected, inherited] |
Vector of pointers to the species databases.
This is used to access data needed to construct the transport manager and other properties later in the initialization process. We create a copy of the XML_Node data read in here. Therefore, we own this data.
Definition at line 2096 of file ThermoPhase.h.
Referenced by ThermoPhase::operator=(), ThermoPhase::saveSpeciesData(), ThermoPhase::speciesData(), and ThermoPhase::~ThermoPhase().
bool m_speciesFrozen [protected, inherited] |
Boolean indicating whether the number of species has been frozen.
During the construction of the phase, this is false. After construction of the the phase, this is true.
Definition at line 359 of file Constituents.h.
Referenced by Constituents::freezeSpecies(), Constituents::operator=(), Constituents::ready(), and Constituents::speciesFrozen().
std::vector<std::string> m_speciesNames [protected, inherited] |
Vector of the species names.
Definition at line 369 of file Constituents.h.
Referenced by Constituents::addUniqueSpecies(), Constituents::operator=(), Constituents::speciesIndex(), Constituents::speciesName(), and Constituents::speciesNames().
vector_fp m_speciesSize [protected, inherited] |
m_speciesSize(): Vector of species sizes.
length m_kk This is used in some equations of state which employ the constant partial molar volume approximation. It's so fundamental we've put it at the Constituents class level
Definition at line 393 of file Constituents.h.
Referenced by Constituents::addUniqueSpecies(), HMWSoln::initLengths(), DebyeHuckel::initLengths(), MineralEQ3::initThermoXML(), HMWSoln::initThermoXML(), DebyeHuckel::initThermoXML(), Constituents::operator=(), Constituents::size(), and DebyeHuckel::standardConcentration().
SpeciesThermo* m_spthermo [protected, inherited] |
Pointer to the calculation manager for species reference-state thermodynamic properties.
This class is called when the reference-state thermodynamic properties of all the species in the phase needs to be evaluated.
Definition at line 2086 of file ThermoPhase.h.
Referenced by SurfPhase::_updateThermo(), SingleSpeciesTP::_updateThermo(), IdealSolidSolnPhase::_updateThermo(), IdealGasPhase::_updateThermo(), IdealGasPhase::entropy_mole(), IdealGasPhase::getEntropy_R(), IdealGasPhase::getGibbs_RT(), IdealGasPhase::getPartialMolarEntropies(), IdealGasPhase::getPureGibbs(), IdealGasPhase::getStandardChemPotentials(), IdealSolidSolnPhase::initLengths(), StoichSubstanceSSTP::initThermo(), SingleSpeciesTP::initThermo(), IdealGasPhase::initThermo(), WaterSSTP::initThermoXML(), ThermoPhase::maxTemp(), ThermoPhase::minTemp(), VPStandardStateTP::operator=(), ThermoPhase::operator=(), ThermoPhase::refPressure(), ThermoPhase::setSpeciesThermo(), ThermoPhase::speciesThermo(), IdealMolalSoln::speciesThermo(), HMWSoln::speciesThermo(), DebyeHuckel::speciesThermo(), and ThermoPhase::~ThermoPhase().
int m_ssConvention [protected, inherited] |
Contains the standard state convention.
Definition at line 2133 of file ThermoPhase.h.
Referenced by ThermoPhase::operator=(), and ThermoPhase::standardStateConvention().
double m_TempPitzerRef [private] |
Reference Temperature for the Pitzer formulations.
Definition at line 2474 of file HMWSoln.h.
Referenced by HMWSoln::constructPhaseXML(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_CoeffWRTemp().
vector_fp m_Theta_ij [mutable, private] |
Array of 2D data for Theta_ij[i][j] in the Pitzer/HMW formulation.
Array of 2D data used in the Pitzer/HMW formulation. Theta_ij[i][j] is the value of the theta coefficient for the ij interaction. It will be nonzero for charged ions with the same sign. It is symmetric. counterIJ where counterIJ = m_counterIJ[i][j] is used to access this array.
HKM Recent Pitzer papers have used a functional form for Theta_ij, which depends on the ionic strength.
Definition at line 2777 of file HMWSoln.h.
Referenced by HMWSoln::HMWSoln(), HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLPsiCommonAnion(), HMWSoln::readXMLPsiCommonCation(), HMWSoln::readXMLThetaAnion(), HMWSoln::readXMLThetaCation(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_lnMolalityActCoeff().
Array2D m_Theta_ij_coeff [private] |
Array of coefficients for Theta_ij[i][j] in the Pitzer/HMW formulation.
Theta_ij[i][j] is the value of the theta coefficient for the ij interaction. It will be nonzero for charged ions with the same sign. It is symmetric. Column index is counterIJ. counterIJ where counterIJ = m_counterIJ[i][j] is used to access this array.
m_Theta_ij_coeff.ptrColumn(counterIJ) is a double* containing the vector of coefficients for the counterIJ interaction.
Definition at line 2809 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::readXMLThetaAnion(), HMWSoln::readXMLThetaCation(), and HMWSoln::s_updatePitzer_CoeffWRTemp().
vector_fp m_Theta_ij_L [mutable, private] |
Derivative of Theta_ij[i][j] wrt T.
vector index is counterIJ
Definition at line 2783 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT().
vector_fp m_Theta_ij_LL [mutable, private] |
Derivative of Theta_ij[i][j] wrt TT.
vector index is counterIJ
Definition at line 2789 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::s_updatePitzer_CoeffWRTemp(), and HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2().
vector_fp m_Theta_ij_P [mutable, private] |
Derivative of Theta_ij[i][j] wrt P.
vector index is counterIJ
Definition at line 2795 of file HMWSoln.h.
Referenced by HMWSoln::initLengths(), HMWSoln::operator=(), and HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP().
doublereal m_Tlast_ss [mutable, protected, inherited] |
The last temperature at which the standard statethermodynamic properties were calculated at.
Definition at line 614 of file VPStandardStateTP.h.
Referenced by VPStandardStateTP::_updateStandardStateThermo(), VPStandardStateTP::operator=(), and VPStandardStateTP::updateStandardStateThermo().
vector_fp m_tmpV [mutable, private] |
vector of size m_kk, used as a temporary holding area.
Definition at line 2573 of file HMWSoln.h.
Referenced by HMWSoln::cv_mole(), HMWSoln::gibbs_mole(), HMWSoln::initLengths(), HMWSoln::operator=(), HMWSoln::relative_enthalpy(), and HMWSoln::standardConcentration().
VPSSMgr* m_VPSS_ptr [mutable, protected, inherited] |
Pointer to the VPSS manager that calculates all of the standard state info efficiently.
Definition at line 631 of file VPStandardStateTP.h.
Referenced by VPStandardStateTP::_updateStandardStateThermo(), IdealSolnGasVPSS::calcDensity(), IdealSolnGasVPSS::cp_mole(), IdealSolnGasVPSS::enthalpy_mole(), IdealSolnGasVPSS::entropy_mole(), IdealSolnGasVPSS::getActivityConcentrations(), VPStandardStateTP::getCp_R(), VPStandardStateTP::getCp_R_ref(), VPStandardStateTP::getEnthalpy_RT(), VPStandardStateTP::getEnthalpy_RT_ref(), VPStandardStateTP::getEntropy_R(), VPStandardStateTP::getEntropy_R_ref(), VPStandardStateTP::getGibbs_ref(), VPStandardStateTP::getGibbs_RT(), VPStandardStateTP::getGibbs_RT_ref(), VPStandardStateTP::getIntEnergy_RT(), VPStandardStateTP::getPureGibbs(), VPStandardStateTP::getStandardVolumes(), VPStandardStateTP::getStandardVolumes_ref(), VPStandardStateTP::initThermo(), VPStandardStateTP::initThermoXML(), VPStandardStateTP::operator=(), VPStandardStateTP::provideVPSSMgr(), IdealSolnGasVPSS::setToEquilState(), VPStandardStateTP::setVPSSMgr(), IdealSolnGasVPSS::standardConcentration(), and VPStandardStateTP::~VPStandardStateTP().
WaterProps* m_waterProps [private] |
Pointer to the water property calculator.
Definition at line 2552 of file HMWSoln.h.
Referenced by HMWSoln::A_Debye_TP(), HMWSoln::d2A_DebyedT2_TP(), HMWSoln::dA_DebyedP_TP(), HMWSoln::dA_DebyedT_TP(), HMWSoln::initThermoXML(), and HMWSoln::operator=().
Water standard state calculator.
derived from the equation of state for water.
Definition at line 2541 of file HMWSoln.h.
Referenced by HMWSoln::initThermoXML(), HMWSoln::operator=(), and HMWSoln::satPressure().
vector_fp m_weight [protected, inherited] |
Vector of molecular weights of the species.
This vector has length m_kk. The units of the vector are kg kmol-1.
Definition at line 352 of file Constituents.h.
Referenced by WaterSSTP::initThermoXML(), Constituents::molecularWeight(), Constituents::molecularWeights(), and Constituents::operator=().
doublereal m_weightSolvent [protected, inherited] |
Molecular weight of the Solvent.
Definition at line 875 of file MolalityVPSSTP.h.
Referenced by MolalityVPSSTP::operator=(), HMWSoln::s_updatePitzer_d2lnMolalityActCoeff_dT2(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dP(), HMWSoln::s_updatePitzer_dlnMolalityActCoeff_dT(), HMWSoln::s_updatePitzer_lnMolalityActCoeff(), and MolalityVPSSTP::setSolvent().
doublereal m_xmolSolventMIN [protected, inherited] |
In any molality implementation, it makes sense to have a minimum solvent mole fraction requirement, since the implementation becomes singular in the xmolSolvent=0 limit. The default is to set it to 0.01. We then modify the molality definition to ensure that molal_solvent = 0 when xmol_solvent = 0.
Definition at line 885 of file MolalityVPSSTP.h.
Referenced by MolalityVPSSTP::calcMolalities(), IdealMolalSoln::getActivities(), MolalityVPSSTP::getActivityCoefficients(), IdealMolalSoln::getMolalityActivityCoefficients(), MolalityVPSSTP::moleFSolventMin(), MolalityVPSSTP::operator=(), IdealMolalSoln::s_updateIMS_lnMolalityActCoeff(), HMWSoln::s_updateIMS_lnMolalityActCoeff(), HMWSoln::s_updatePitzer_lnMolalityActCoeff(), MolalityVPSSTP::setMolalitiesByName(), and MolalityVPSSTP::setMoleFSolventMin().
doublereal MC_apCut_ [private] |
Parameter in the Molality Exp cutoff treatment.
Definition at line 3304 of file HMWSoln.h.
Referenced by HMWSoln::calcMCCutoffParams_(), and HMWSoln::operator=().
doublereal MC_bpCut_ [private] |
Parameter in the Molality Exp cutoff treatment.
Definition at line 3307 of file HMWSoln.h.
Referenced by HMWSoln::calcMCCutoffParams_(), and HMWSoln::operator=().
doublereal MC_cpCut_ [private] |
Parameter in the Molality Exp cutoff treatment.
Definition at line 3310 of file HMWSoln.h.
Referenced by HMWSoln::calcMCCutoffParams_(), and HMWSoln::operator=().
doublereal MC_dpCut_ [private] |
Parameter in the Molality Exp cutoff treatment.
Definition at line 3298 of file HMWSoln.h.
Referenced by HMWSoln::calcMCCutoffParams_(), and HMWSoln::operator=().
doublereal MC_epCut_ [private] |
Parameter in the Molality Exp cutoff treatment.
Definition at line 3301 of file HMWSoln.h.
Referenced by HMWSoln::calcMCCutoffParams_(), and HMWSoln::operator=().
doublereal MC_slopepCut_ [private] |
Parameter in the Molality Exp cutoff treatment.
This is the slope of the p function at the zero solvent point Default value is 0.0
Definition at line 3295 of file HMWSoln.h.
Referenced by HMWSoln::calcMCCutoffParams_(), and HMWSoln::operator=().
doublereal MC_X_o_cutoff_ [private] |
value of the solvent mole fraction that centers the cutoff polynomials for the cutoff =1 process;
Definition at line 3285 of file HMWSoln.h.
Referenced by HMWSoln::calcMCCutoffParams_(), and HMWSoln::operator=().
doublereal MC_X_o_min_ [private] |
gamma_o value for the cutoff process at the zero solvent point
Definition at line 3288 of file HMWSoln.h.
Referenced by HMWSoln::calcMCCutoffParams_(), and HMWSoln::operator=().
std::vector<doublereal> xMol_Ref [protected, inherited] |
Reference Mole Fraction Composition.
Occasionally, the need arises to find a safe mole fraction vector to initialize the object to. This contains such a vector. The algorithm will pick up the mole fraction vector that is applied from the state xml file in the input file
Definition at line 2142 of file ThermoPhase.h.
Referenced by ThermoPhase::getReferenceComposition(), ThermoPhase::initThermo(), and ThermoPhase::setReferenceComposition().
The documentation for this class was generated from the following files:
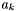 of a species in solution is related to the chemical potential by
of a species in solution is related to the chemical potential by ![\[ \mu_k = \mu_k^0(T) + \hat R T \log a_k. \]](form_98.png)
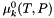 is the chemical potential at unit activity, which depends only on temperature and the pressure.
is the chemical potential at unit activity, which depends only on temperature and the pressure.![\[ \mu_k = \mu_k^0(T,P) + \hat R T \log a_k. \]](form_478.png)
 1.6.3
1.6.3